II. Задание к контрольной работе по дискретной математике
I. Множества и операции над ними.
1) Для заданных множеств А, В и С найти:
 B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А Å B, А Å С, B Å C, A Å B Å C. Изобразить на плоскости
B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А Å B, А Å С, B Å C, A Å B Å C. Изобразить на плоскости  Найти
Найти  считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
2) Докажите тождество, используя диаграммы Эйлера – Венна.
II. Отношения. Функции. Отношения эквивалентности и упорядоченности.
1) Даны множества  и два бинарных отношения:
и два бинарных отношения:  и
и  . Изобразите Р1, Р2 графически. Найдите Р1-1, Р2-1,
. Изобразите Р1, Р2 графически. Найдите Р1-1, Р2-1,  Определите, является ли отношение Р2 рефлексивным, транзитивным, симметричным, антисимметричным.
Определите, является ли отношение Р2 рефлексивным, транзитивным, симметричным, антисимметричным.
2) Даны отображения (числовые функции) ƒ, g: ℝ→ℝ. Найти композицию ƒ ◦ g, g ◦ ƒ, обратные отображения: ƒ–1, g-1, (ƒ ◦ g)-1, (g ◦ ƒ)-1. Для заданных множеств A, B Í ℝ найти f(A), g(A), ƒ –1(B), g-1(B). Найти неподвижные точки отображений.
III. Функции и формулы алгебры логики. Эквивалентность формул.
1) Составьте полную и сокращенную таблицы истинности формул.
2) Проверьте двумя способами, будут ли эквивалентны следующие формулы: а) составлением таблиц истинности; б) с помощью эквивалентных преобразований.
III. Варианты контрольных работ
Вариант №1
I.1. А = [-3; 0] – отрезок числовой оси
В = (-1; 3] – полуинтервал на числовой оси
С = (-0.5; 4) – интервал на числовой оси
2. 
II.1. Р1 = {(а, 2); (а, 3); (а, 4); (b, 3); (с, 1); (с, 4)}
Р2 = {(1, 1); (2, 3); (2, 2); (3, 4); (1, 4); (2, 4); (4, 2)}
2. f(x) = –(x + 1)2; g(x) = –x –2; А = [–1.5; 1]; В = [–2; –1]
III.1. 
2. x → (y ↓ z) и (x → y ) ↓ (x → z)
Вариант №2
I.1. А = (0; 10] – полуинтервал на числовой оси
В = [–1; 5] – отрезок числовой оси
С = (–10; 2) – интервал на числовой оси
2. (А \ В)  (В \ С)
(В \ С)  (В \ А)
(В \ А)  (С \ В) = А
(С \ В) = А  С
С
II.1. Р1 = {(b, 2); (а, 3); (b, 1); (b, 4); (с, 1); (с, 2); (с, 4)}
Р2 = {(1, 1); (1, 2); (1, 4); (2, 2); (2, 4); (3, 3); (3, 2); (3, 4); (4, 4)}
2. f(x) = (x + 1)2 – 1; g(x) = x + 1; А = [–1.5; 1]; В = [0; 1]
III.1. 
2. x → (y ≡ z) и (x → y ) ≡ (x → z)
Вариант №3
I.1. А = {0, 1, 2, 3}– четырехэлементное множество
В = [–5; 3] – отрезок числовой оси
С = (0; 2) – интервал на числовой оси
2. (А \ В)  (В \ С)
(В \ С)  (С \ А) = (В \ А)
(С \ А) = (В \ А)  (С \ В)
(С \ В)  (А \ С)
(А \ С)
II.1. Р1 = {(а, 3); (а, 2); (а, 4); (b 1); (с, 2); (с, 4); (с, 3)}
Р2 = {(1, 1); (2, 2); (2, 1); (3, 3); (4, 4); (4, 3); (1, 4); (2, 4); (3, 2); (3, 4)}
2. f(x) = (x + 1)2 + 1; g(x) = x + 3; А = [–1.5; 1]; В = [2; 3]
III.1. 
2. x ≡ (y | z) и (x ≡ y) | (x ≡ z)
Вариант №4
I.1. А = (–1; +∞)– интервал на числовой оси
В = (–10; 10] – полуинтервал на числовой оси
С = [–5; +15] – отрезок числовой оси
2. (А  В)
В)  (С
(С  D) = В
D) = В  С, если А
С, если А  В = D и C
В = D и C  D = A
D = A
II.1. Р1 = {(b, 1); (а, 3); (а, 4); (с, 2); (с, 4); (b, 4)}
Р2 = {(1, 1); (2, 3); (2, 2); (2, 4); (3, 3); (3, 4); (4, 2); (4, 4)}
2. f(x) = (x + 1)2; g(x) = x + 2; А = [–1.5; 1]; В = [1; 2]
III.1. 
2. x ↓ (y | z) и (x ↓ y) | (x ↓ z)
Вариант №5
I.1. А = (–16; 8]– полуинтервал на числовой оси
В = [–9; 9] – отрезок числовой оси
С = (5; +∞) – интервал на числовой оси
2. (А \ (В \ С)) \ ((А \ В)\ С) = А  С
С
II.1. Р1 = {(а, 2); (а, 4); (b, 1); (b, 2); (b, 4); (с, 2); (с, 4)}
Р2 = {(1, 1); (2, 2); (2, 4); (3, 3); (4, 4); (3, 2); (1, 3); (4, 1)}
2. f(x) = (x – 1)2 – 1; g(x) = x – 1; А = [0.5; 3]; В = [0; 1]
III.1. 
2. x → (y ↓ z) и (x → y) | (x → z)
Вариант №6
I.1. А = [–25; 1]– отрезок числовой оси
В = {–1; 0; 1} – трехэлементное множество
С = (0; +∞) – интервал на числовой оси
2. (А \ В)  (В \ А) = А
(В \ А) = А  В
В
II.1. Р1 = {(а, 2); (а, 4); (а, 3); (с, 1); (с, 2); (с, 3)}
Р2 = {(1, 1); (1, 4); (2, 3); (3, 3); (4, 1); (4, 3); (4, 4)}
2. f(x) = (x – 1)2 + 1; g(x) = x + 1; А = [0.5; 3]; В = [2; 3]
III.1. 
2. x ≡ (y  z) и (x ≡ y)
z) и (x ≡ y)  (x ≡ z)
(x ≡ z)
Вариант №7
I.1. А = (–10; 5]– полуинтервал на числовой оси
В = [0; 10] – отрезок числовой оси
С = (4; +∞) – интервал на числовой оси
2. ((А  В) \ С) = (А \(В
В) \ С) = (А \(В  С))
С))  (В \(А
(В \(А  С))
С))
II.1. Р1 = {(а, 1); (b, 2); (b, 3); (с, 1); (с, 3); (с, 4)}
Р2 = {(1, 1); (1, 2); (1, 3); (2, 2); (2, 3); (3, 3); (3, 4); (4, 1); (4, 4)}
2. f(x) = (x – 1)2; g(x) = x; А = [0.5; 3]; В = [1; 2]
III.1. 
2. x ↓(y  z) и (x ↓y)
z) и (x ↓y)  (x ↓ z)
(x ↓ z)
Вариант №8
I.1. А = (–∞; 2]– полуинтервал на числовой оси
В = [–3; 3] – отрезок числовой оси
С = (0; 4) – интервал на числовой оси
2. 
II.1. Р1 = {(а, 3); (b, 4); (b, 3); (с, 1); (с, 2); (с, 4)}
Р2 = {(1, 2); (1, 3); (1, 4); (2, 3); (4, 3); (4, 2)}
2. f(x) = – (x + 1)2 –1; g(x) = x–1; А = [–1.5; 1]; В = [–3; –2]
III.1. 
2. x 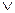 (y
(y  z) и (x
z) и (x 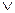 y)
y)  (x
(x 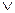 z)
z)
Вариант №9
I.1. А = (–2; 3) – интервал на числовой оси
В = [0; 4] – отрезок числовой оси
С = {2; 3} – двухэлементное множество
2. 
II.1. Р1 = {(а, 3); (b, 4); (b, 3); (b, 1); (b, 2); (c, 2)}
Р2 = {(1, 1); (1, 3); (2, 4); (3, 1); (3, 3); (4, 2)}
2. f(x) = 1– (x + 1)2; g(x) = x+1; А = [–1.5; 1]; В = [–1; 0]
III.1. 
2. x → (y ≡ z) и (x →y) ≡ (x → z)
Вариант №10
I.1. А = [–7.5; 4.5]– отрезок числовой оси
В = (0; 5)– интервал на числовой оси
С = (–10; 0] – полуинтервал на числовой оси
2. 
II.1. Р1 = {(а, 2); (а, 3); (a, 4); (b, 1); (b, 2); (b, 4)}
Р2 = {(1, 1); (1, 3); (1, 4); (2, 2); (2, 3); (3, 2); (3,3); (4,3); (4,4)}
2. f(x) = – (x – 1)2 –1; g(x) = x–3; А = [0.5; 3]; В = [–3; –2]
III.1. 
2. x → (y | z) и (x →y) | (x → z)
Вариант №11
I.1. А = (–5; 5]– полуинтервал на числовой оси
В = (0; +∞)– интервал на числовой оси
С = {–1; 0; 1} – трехэлементное множество
2. 
II.1. Р1 = {(а, 1); (а, 2); (b, 3); (b, 4); (c, 3); (c, 4)}
Р2 = {(1, 1); (1, 4); (2, 1); (2, 2); (2, 4); (3, 3)}
2. f(x) = 1– (x – 1)2; g(x)= x–1; А = [0.5; 3]; В = [–1; 0]
III.1. 
2. x | (y  z) и (x | y)
z) и (x | y)  (x | z)
(x | z)
Вариант №12
I.1. А = (–12; 12)– интервал на числовой оси
В = [10; 20] – отрезок числовой оси
С = (–∞; +15] - полуинтервал на числовой оси
2. 
II.1. Р1 = {(а, 2); (а, 3); (а, 4); (с, 3); (c, 1); (c, 4)}
Р2 = {(1, 4); (2, 3); (2, 1); (3, 4); (4, 2)}
2. f(x) = – (x – 1)2; g(x)= x; А = [–1.5; 1]; В = [–2; –1]
III.1. 
2. 
Вариант №13
I.1. А = (5; 15] – полуинтервал на числовой оси
В = [5; 10] – отрезок числовой оси
С = {4; 5; 6} – трехэлементное множество
2. 
II.1. Р1 = {(а, 1); (а, 2); (а, 4); (b, 2); (b, 4); (c, 3)}
Р2 = {(1, 1); (2, 2); (2, 4); (3, 3); (4, 4);(4,2)}
2. f(x) = – (x – 1)2; g(x)= x – 2; А = [0.5; 3]; В = [–2; –1]
III.1. 
2. 
Вариант №14
I.1. А = (0; + ∞) – интервал на числовой оси
В = [–3; 3] – отрезок числовой оси
С = (–10; 0] - полуинтервал на числовой оси
2. 
II.1. Р1 = {(b, 1); (b, 3); (c, 1); (c, 2); (c, 3); (c, 4)}
Р2 = {(1, 1); (2, 2); (2, 3); (2, 4); (3, 2); (3, 3); (3, 4); (4, 2); (4, 3); (4, 4)}
2. f(x) = (x+ 1)2–1; g(x)= –x – 1; А = [–1.5; 1]; В = [0; 1]
III.1. 
2. 
Вариант №15
I.1. А = [–5; 25) – полуинтервал на числовой оси
В = [–25; 5] – отрезок числовой оси
С = (–10; 15) - интервал на числовой оси
2. 
II.1. Р1 = {(a, 2); (a, 4); (b, 3); (c, 1); (c, 2)}
Р2 = {(1, 1); (1, 3); (2, 4); (3, 1); (3, 4); (4, 3); (4, 2)}
2. f(x) = (x+ 1)2 +1; g(x)= 1– x; А = [–1.5; 1]; В = [2; 3]
III.1. 
2. 
Вариант №16
I.1. А = (0; 25) – интервал на числовой оси
В = {0; 1; 2} – трехэлементное множество
С = [–1; 1] - отрезок числовой оси
2. 
II.1. Р1 = {(а, 3); (а, 2); (b, 2); (b, 3); (c, 1); (c, 4)}
Р2 = {(1, 1); (1, 2); (2, 2); (3, 3); (4, 1); (4, 4)}
2. f(x) = (x – 1)2 –1; g(x)= 1 – x; А = [0.5; 3]; В = [0; 1]
III.1. 
2. 
Вариант №17
I.1. А = [–7; 7] – отрезок числовой оси
В = [0; +∞) – полуинтервал на числовой оси
С = (–∞; 5) - интервал на числовой оси
2. 
II.1. Р1 = {(а, 1); (а, 2); (а, 4); (b, 3); (c, 1); (c, 4)}
Р2 = {(1, 3); (1, 2); (2, 3); (3, 2); (3, 4); (4, 1)}
2. f(x) = (x – 1)2 +1; g(x)= 3 – x; А = [0.5; 3]; В = [2; 3]
III.1. 
2. 
Вариант №18
I. 1. А=[–  ; 3) – полуинтервал на числовой оси
; 3) – полуинтервал на числовой оси
В=[3; 10] – отрезок числовой оси
С=(3; +  ) – интервал на числовой оси
) – интервал на числовой оси
2. (A  (A \ B))
(A \ B)) 
 = Æ
= Æ
II. 1. P1={ (a, 1); (b, 3); (c; 1); (c, 4); (c, 3); (c, 2)}
 P2={(1, 1); (1, 2); (1, 4); (2, 1); (2, 2); (2, 3); (3, 3); (3, 2); (3, 4); (4, 3); (4, 4); (4, 1)}
P2={(1, 1); (1, 2); (1, 4); (2, 1); (2, 2); (2, 3); (3, 3); (3, 2); (3, 4); (4, 3); (4, 4); (4, 1)}
2. f (x)=(x+1)2; g(x)= –x; A=[–1.5; 1]; B= [1; 2]
III. 1. (х 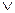 y)
y) 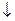 (y
(y  ); (x
); (x 
 )
)  (z |
(z |  )
)
2. x 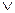 (y
(y  z) и (x
z) и (x 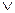 y)
y)  (x
(x 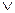 z)
z) 
Вариант №19
I. 1. А=[–11; 11] –отрезок числовой оси
В=[–12; 3) – полуинтервал на числовой оси
С=(0; 12) – интервал на числовой оси
2. ((A  C)
C)  (B
(B  D))
D)) 
II. 1. P1={(a, 1); (b, 3); (b, 1); (b, 4); (c, 3); (c, 2)}
 P2={(1, 3); (1, 4); (2, 2); (3, 3); (4, 3); (4, 4);}
P2={(1, 3); (1, 4); (2, 2); (3, 3); (4, 3); (4, 4);}
2. f (x)=(x – 1)2; g(x)=2– x; A=[0.5; 3]; B=[1; 2]
III. 1. 
2. 
Вариант №20
I. 1. А=(–10; 1) –интервал на числовой оси
В={–1; 0; 1} – трехэлементное множество
С=[0.5; 10] – отрезок числовой оси
2. 
II. 1. P1={(a, 1); (a, 2); (a; 4); (b, 1); (b, 4); (c, 3)}
 P2={(1, 1); (2, 4); (2, 1); (3, 3); (4, 2); (4, 1)}
P2={(1, 1); (2, 4); (2, 1); (3, 3); (4, 2); (4, 1)}
2. f (x)= –x2 – 1; g(x)= –x – 3; A=[–0.5; 2]; B=[–3; –1]
III. 1 
2. 
Вариант №21
I. 1. А=[10; 20] – отрезок числовой оси
В=(0; 15) – интервал на числовой оси
С={5; 10; 15} – трехэлементное множество
2. 
II. 1. P1={(a, 1); (a, 4); (b, 2); (b, 3); (c, 1); (c, 4)}
 P2={(1, 1); (1, 4); (2, 1); (3, 4); (4, 3); (4, 1)}
P2={(1, 1); (1, 4); (2, 1); (3, 4); (4, 3); (4, 1)}
2. f (x)= 1–x2; g(x)= –x – 1; A=[–0.5; 2]; B=[–1; 0]
III. 1 
2. 
Вариант №22
I. 1. А= {–1; 0; 1} – трехэлементное множество
В=(–10; 0.5) – интервал на числовой оси
С=[0; 10] – отрезок числовой оси
2. 
II. 1. P1={(a, 1); (a, 2); (b, 2); (b, 4); (c, 3); (c, 2)}
 P2={(1, 1); (1, 2); (2, 2); (3, 3); (4, 3); (4,4)}
P2={(1, 1); (1, 2); (2, 2); (3, 3); (4, 3); (4,4)}
2. f (x)= –x2; g(x)= –x – 2; A=[–0.5; 2]; B=[–2; –1]
III. 1. 
2. 
Вариант №23
I. 1. А= [–6; +6) - полуинтервал
В=[–10; 2] –отрезок
С=(2; 10) – интервал
2. 
II. 1. P1={(a, 1); (a, 2); (a, 4); (c, 3); (c, 2); (c, 4)}
 P2={(2, 1); (3, 1); (3, 2); (4, 1); (4, 3)}
P2={(2, 1); (3, 1); (3, 2); (4, 1); (4, 3)}
2. f(x)= x2; g(x)= 2–x; A=[–0.5; 2]; B=[1; 2]
III. 1. 
2. 
Вариант №24
I. 1. А= (–10; 4) – интервал на числовой оси
В=[0; 10] – отрезок числовой оси
С=(2; 7] – полуинтервал на числовой оси
2. 
II. 1. P1={(a, 1); (a, 2); (a, 3); (a, 4); (b, 3); (c, 2)}
 P2={(1, 1); (1, 4); (2, 2); (2, 3); (3, 3); (3, 2); (4, 1); (4, 4)}
P2={(1, 1); (1, 4); (2, 2); (2, 3); (3, 3); (3, 2); (4, 1); (4, 4)}
2. f(x)= x2 +1; g(x)= –x; A=[–0.5; 2]; B=[2; 3]
III. 1. 
2. 
Вариант №25
I. 1. А= (2; 15] – полуинтервал на числовой оси
В=[–5; 5] – отрезок числовой оси
С=(–10; 3) – интервал на числовой оси
2. 
II. 1. P1={(a, 1); (a, 2); (b, 3); (c, 2); (c, 3); (c, 4)}
 P2={(1, 1); (2, 1); (2, 2); (2, 3); (2, 4); (3, 3); (4, 4)}
P2={(1, 1); (2, 1); (2, 2); (2, 3); (2, 4); (3, 3); (4, 4)}
2. f (x)= x2–1; g(x)=1– x; A=[–0.5; 2]; B=[0; 1]
III. 1. 
2. 
