Необходимо сделать эту распечатку!

Прокрутить вниз – нажать два раза Esc – нажать F1 – стереть Backspace – написать новое имя – нажать Enter – нажать 1,2,3,4,5 – нажать Enter – искать файл в папке.

МЕСТО ДЛЯ РАСПЕЧАТКИ (с DELTA=-96,039)

2 Способ:

Нам нужна распечатка для второго конденсора, первая, которая не с Delta.

Находим там этот момент:

Осевой пучок ____Л0____ ____Л1____ ____Л2____

== M = 100tg б'== dS'=== dY'=== dS'=== dY'=== dS'=== dY'= dS'12 = Eta %=

21.254 18.29 -112.47 -20.573-115.92-21.771-108.85-19.383-7.0789 45.756

18.406 13.89 -90.755 -12.606-94.995-13.569-86.289-11.647-8.7057 37.252

15.026 9.95 -65.833 -6.5521-71.115-7.2949-60.236-5.8118-10.879 27.244

10.627 6.16 -36.306 -2.2353-43.015-2.7375-29.150-1.7344-13.865 15.140

0.000 0.00 -0.0000 0.0000-8.7341 0.0000 9.3972 0.0000-18.131

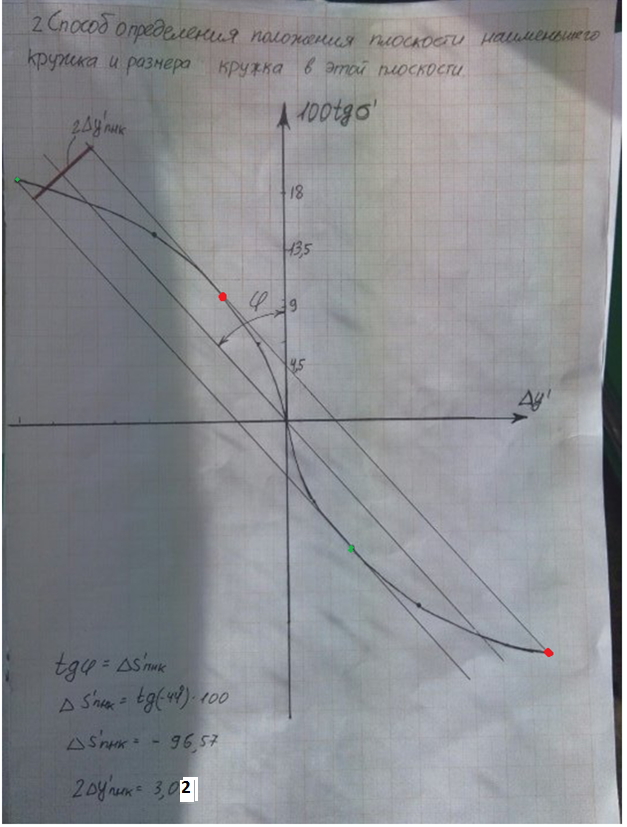
Строим график: по оси ox откладываем dY’

по оси oy откладываем 100tgσ’

Делаем график симметричным.

Проводим 3 касательные. Сначала проводится касательная от последней точки графика (в нижней правой части) до крайней точки графика (в верхней левой части).Выделил это точки красным цветом.

Потом касательную через центр, параллельную первой касательной.

Третья так же, как и первая. Выделил зеленым цветом.

Отметим угол 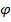. Если вы защищаете работу и вас спросили, как вы померили этот угол, то скажите:
Поделил противолежащий катет на гипотенузу. Для профессионалов математики:

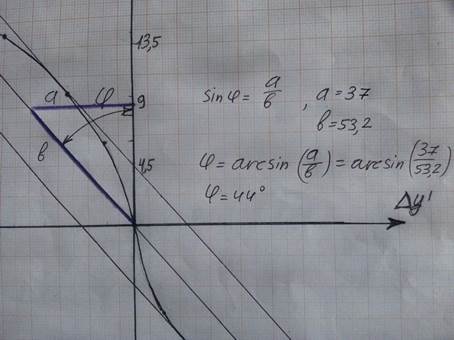
Место измерения кружка рассеяния видно на рисунке.

Измерим весь отрезок линейкой – 26,6 мм

Масштаб в данном случае 4,4:1 (у нас в 80 мм помещается 18, значит, 80/18=4,4)

Истинное значение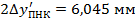

В свою очередь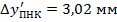

Аберрационный анализ

Так как мениск не вносит сферической аберрации, то аберрации всей системы определяются аберрациями линзы, стоящей после мениска.

Определение продольной сферической аберрации третьего порядка:

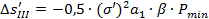, где ,

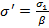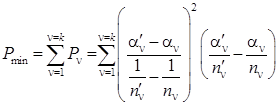
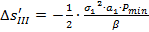
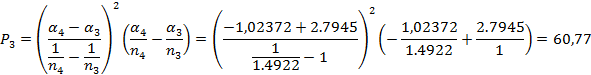
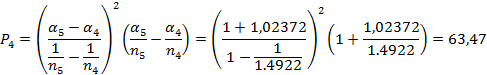
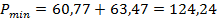
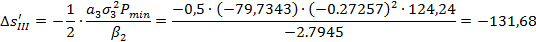
Определение поперечной сферической аберрации:

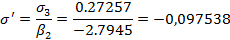
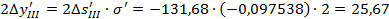
Кружок рассеяния в плоскости наименьшего кружка:

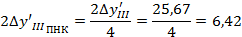
Оценка качества изображения

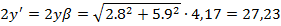
Для тонкой системы:

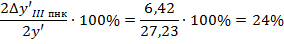
Для реальной системы (графически определили размер наименьшего кружка):

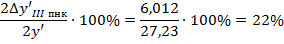
2.8 Определение эффективного увеличения в плоскости наименьшего кружка

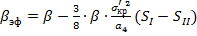, где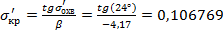

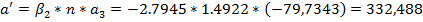
Чтобы посчитать эффективное увеличение, необходимо ввести систему без толщин (оставить толщину только мениска) и в отрезке s1 написать значение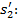

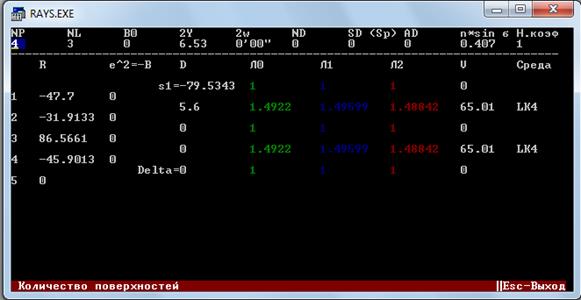
Нажимаем Esc и F9:

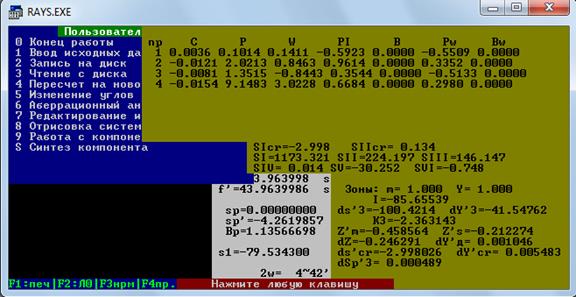
Нам нужны значения 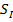и 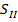: 1173,32 и 224,20

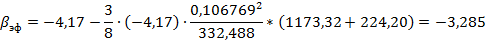
Вывод:

В данной работе был выполнен расчет двух конденсорных систем из двух линз: двух плосковыпуклых и апланатического мениска с линзой, рассчитанной на минимум сферической аберрации. Так же стоит заметить, что был взят достаточно большой угол охвата ( 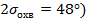, для более видимых значений аберраций 3-его порядка.
Аберрационный анализ в тонких компонентах показал, что конденсор из двух плосковыпуклых линз имеет большие значения сферической аберрации. Связано это с тем, что для конденсора, состоящего из двух плосковыпуклых линз, не свойственно такое увеличение 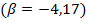, а свойственно 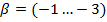, вследствие чего значения аберраций выше.
В отношении качества изображения конденсор, состоящий из апланатического мениска и линзы, рассчитанной на минимум сферической аберрации, вполне удовлетворяет требованиям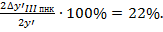

Это вывод по данной работе! Обычно данные такие, что ситуация обратная:

В данной работе был выполнен расчет двух конденсорных систем из двух линз: двух плосковыпуклых и апланатического мениска с линзой, рассчитанной на минимум сферической аберрации. Так же стоит заметить, что был взят достаточно большой угол охвата( 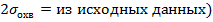, для более видимых значений аберраций 3-его порядка.
Аберрационный анализ в тонких компонентах показал, что конденсор из двух плосковыпуклых линз имеет меньшие значения сферической аберрации. Связано это с тем, что для конденсора с апланатическим мениском и линзой, рассчитанной на минимум сферической аберрации, не свойственно такое увеличение ( 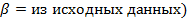, а свойственно 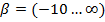, вследствие чего значения аберраций выше.
В отношении качества изображения конденсор из двух плосковыпуклых линз вполне удовлетворяет требованиям качества для обычных конденсорных систем

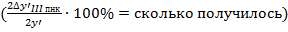, в отличие от результатов у второго конденсора.