Расчет напряженно-деформированного состояния
Для учета наличия лопатки в диске, лопатка моделируется точечной массой. Эта масса привязана к рабочим поверхностям зубцов замка (рис. 9.7.).
Рис. 9.7. Положение точечной массы в расчетной модели.
Координаты точечной массы (0,3638; 7,325е-002; 2е-004) м, масса 169 гр., так как задача статическая, моментами инерции лопатки решено пренебречь.
Расчет напряженно-деформированного состояния диска произведен в модуле Static Structural. Конечноэлементная сетка (рис. 9.8.) неструктурированная состоит из гексагональных элементов. Сетка построена автоматическим сеткопостроителем. Настройки сеткопостроителя сведены в табл. 9.2.
Таблица 9.2.
| Object Name | Mesh |
| State | Solved |
| Defaults | |
| Physics Preference | Mechanical |
| Relevance | |
| Sizing | |
| Use Advanced Size Function | On: Proximity and Curvature |
| Relevance Center | Coarse |
| Initial Size Seed | Active Assembly |
| Smoothing | High |
| Transition | Fast |
| Span Angle Center | Coarse |
| Curvature Normal Angle | 90,0 ° |
| Proximity Accuracy | 0,5 |
| Num Cells Across Gap | |
| Min Size | Default (1,5514e-004 m) |
| Proximity Min Size | Default (1,5514e-004 m) |
| Max Face Size | 2,e-003 m |
| Max Size | Default (3,1027e-002 m) |
| Growth Rate | Default (1,850 ) |
| Minimum Edge Length | 2,618e-004 m |
| Inflation | |
| Use Automatic Inflation | None |
| Inflation Option | Smooth Transition |
| Transition Ratio | 0,272 |
| Maximum Layers | |
| Growth Rate | 1,2 |
| Inflation Algorithm | Pre |
| View Advanced Options | No |
| Patch Conforming Options | |
| Triangle Surface Mesher | Program Controlled |
| Advanced | |
| Shape Checking | Standard Mechanical |
| Element Midside Nodes | Program Controlled |
| Straight Sided Elements | No |
| Number of Retries | |
| Extra Retries For Assembly | Yes |
| Rigid Body Behavior | Dimensionally Reduced |
| Mesh Morphing | Disabled |
| Defeaturing | |
| Pinch Tolerance | Default (1,3962e-004 m) |
| Generate Pinch on Refresh | No |
| Automatic Mesh Based Defeaturing | On |
| Defeaturing Tolerance | Default (7,7568e-005 m) |
Модель диска с наложенной конечноэлементной сеткой представлена на рис. 9.8.
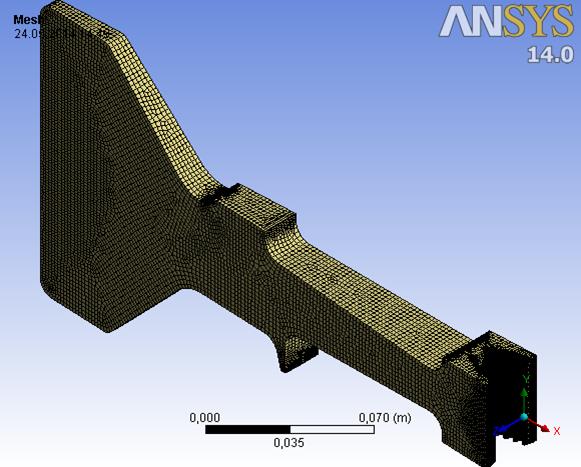
Рис. 9.8. Модель диска с наложенной сеткой.
Количество узлов сетки равно 571113; количество элементов рано 157887.
Внешние нагрузки и закрепления представлены на рис. 9.9.
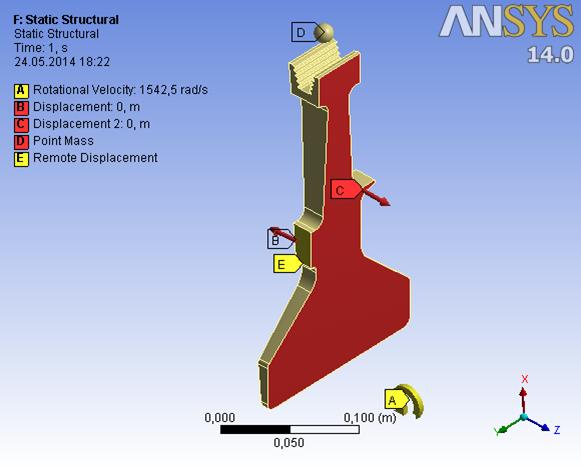
Рис. 9.9. Внешние нагрузки и закрепления.
Закрепления:
· Запрет перемещений поверхности E по оси Y. Все остальные степени свободы не закреплены.
· Запрет перемещений узлов на поверхностях B и С но нормали к этим поверхностям. Таким способам моделируется условие симметрии напряжений сектора диска.
Внешние нагрузки:
· Вращение вокруг оси Y с угловой скоростью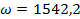 
рад/с.
· Поле температур из предыдущего расчета теплового состояния.
В результате проведения расчета получены распределения абсолютных деформаций (рис. 9.10 ), эквивалентных напряжений(рис. 9.11.), пластических деформаций(рис 9.12.).
Рис. 9.10. Абсолютные деформации диска.
Рис. 9.11. Эквивалентные напряжения.
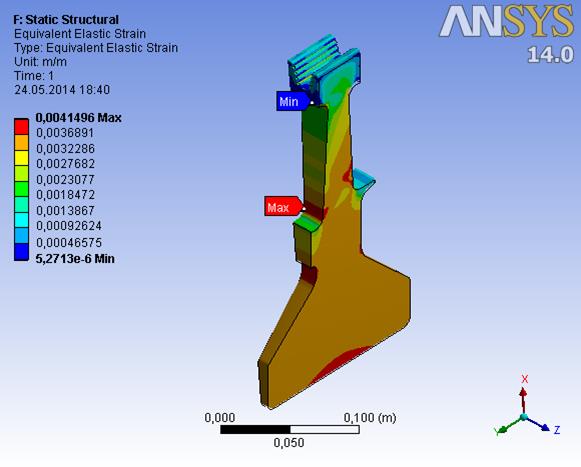
Рис. 9.12. Пластические деформации.
Необходимо отметить, что пластические деформации не превышаю 0,4 %.
Максимальное значение эквивалентных напряжений составляет 864 МПа, в зоне, где температура не превышает 250о С. Предел прочности материала при такой температуре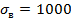 
МПа.
Запас прочности по разрушающим напряжениям можно рассчитать по формуле:
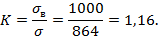
Согласно [3] запас прочности диска по разным оценкам составляет 1,3...1,8. Следовательно запас прочности диска ниже минимально допустимого значения, следовательно необходимо соответствующим образом скорректировать его конструкцию.
Приложение 1
