III. Сообщения кафедр
Кафедра «Истории математики»
Кафедра « Вычислительной и прикладной математики»
Кафедра «Исследования и анализа»
II Конкурс на соответствие
Как в любом научно- исследовательском заведении в начале проведём конкурс на соответствие, т.е. проверим уровень математической подготовки членов кафедр по данному вопросу.
Я задаю вопросы, вы должны будете поднять сигнальную карточку красного цвета, если ответ положительный или белую , если – отрицательный.
1) сумма первого и второго членов геометрической прогрессии равна нулю, а произведение их равно 4. Можно ли задать такую геометрическую прогрессию? (нет)
2) может ли сумма п первых членов арифметической прогрессии быть 0 ? (да)
3) сумма первого и второго членов арифметической прогрессии равна 0, а частное их равно 1. Можно ли задать такую арифметическую прогрессию? (да)
4) является ли последовательность (Сn) – арифметической прогрессией, если равенство Сп= 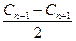 верно для любого n большего 0 (да)
верно для любого n большего 0 (да)
5) может ли сумма п первых членов геометрической прогрессии (q≠1) быть нулём ? (нет)
6) является ли последовательность (Сп) геометрической прогрессией n больше 1), если верно равенство С2n= Сn-1*Сn+2 ? (да)
Итогитак мы проверили уровень подготовки членов кафедр по данной теме. Можно сделать вывод, что сотрудники в основном соответствуют предъявленным требованиям. Подготовились к заседанию хорошо.
III. Сообщения кафедр.
Итак можно переходить к следующему этапу заседания ученого совета. Прослушаем сообщения кафедр по изучаемому вопросу.
1. первым заслушаем кафедру «Истории математики»
понятие числовой последовательности возникло и развивалось задолго до создания учения о функциях.
Сведения связанные с прогрессиями впервые встречаются в дошедших до нас документах Древней Греции. Уже в 5 веке до н. э. греки знали следующие прогрессии и их суммы:
1) 1+2+3+…+n = 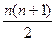 последовательность натуральных чисел.
последовательность натуральных чисел.
2) 2+4+6+…+ 2n = n(n+1)
В 78 веке в английских и французских учебниках появились обозначения арифметической и геометрической прогрессии.
Некоторые формулы , относящиеся к прогрессиям , были известны китайским и индийским ученым. Например, Ариабхатта (5 в. ) знал формулы для общего члена суммы арифметической прогрессии.
Слово «прогрессия» с латинского означает «движение вперед» (как и слово прогресс) встречается впервые у римского автора Боэция .
Из одной клинописной таблички можно заключить, что наблюдая Луну от новолуния до полнолуния вавилоняне пришли к такому выводу :
В первые 5 дней после новолуния рост освещения лунного диска совершается по закону геометрической прогрессии со знаменателем 2.
Впервые задачи на прогрессии возникли из наблюдения над явлениями природы и из исследования общественно-экономических явлений, к которым применим закон арифметической и геометрической прогрессий.
Первоначально под прогрессией понимали всякую числовую последовательность. В конце средних веков этот термин перестал быть общеупотребляемым.
В конце 17 века Грегори употребляет термин «ряд». Другой видный английский математик Джон Валлис применяет для бесконечных рядов термин «бесконечные прогрессии».
В настоящее время мы рассматриваем прогрессии как частные случаи числовых последовательностей.
Спасибо кафедре «истории математики» за интересное сообщение.
Слушаем кафедру «исследования и анализа».
2. Выступление кафедры «исследования и анализа»:
Почитав подряд определения арифметической и геометрической прогрессий, мы обратили внимание на то, что они похожи. Надо лишь заменить сложение умножением или наоборот. А зная формулу n-го члена арифметической прогрессии, можно получить формулу для n-го члена геометрической прогрессии, если заменить сложение умножением, а умножение возведем в степень:
ап = а1+(n-1)d вп = в1qп—1
На связь между прогрессиями первым обратил внимание Архимед.
В 1544г вышла книга немецкого математика Штифеля «Общая арифметика», который составил такую таблицу:
| -4 | -3 | -2 | -1 | 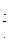 | D=1 | ||||||||
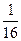 | 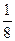 | 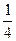 | 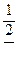 | 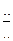 | Q=2 |
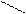 нулю арифметической прогрессии соответствует 1 геометрической прогрессии. Это очень важный факт. Выясним связь между этими прогрессиями. Например, нужно умножить 128 над ½. написано -1, над 128 написано 7, сложим эти числа -1+7=6
нулю арифметической прогрессии соответствует 1 геометрической прогрессии. Это очень важный факт. Выясним связь между этими прогрессиями. Например, нужно умножить 128 над ½. написано -1, над 128 написано 7, сложим эти числа -1+7=6
под числом 6 находится 64. это и есть искомое произведение.
Применяя тождества умножения и деления степеней аn *аm = аn+m, аn/аm = аn-m, то нижнюю строчку таблицы Штифеля можно переписать так:
2-4, 2-3, 2-2, 2-1, 20, 21,22, 23, 24,25, 26, 27.
Нетрудно сообразить: 2-1*27=26
Делаем вывод:
Если показатели составляют арифметическую прогрессию, то сами степени составляю геометрическую прогрессию.
Спасибо кафедре «исследования и анализа» за интересное сообщение.
3. слушаем кафедру «вычислительной и прикладной математики»:
Мы приготовили задания для устного решения .
1) (Сп)- арифметическая прогрессия., с1= 20, d=3 найти с5-?
С5 = с1 + 4d = 20 + 4*3 = 32
2) (хп)- геометрическая прогрогрессия, х1= 32, q=1/2 , найти х5?
Х5 = х1*q4 = 32*(1/2)4 = 32/16 = 2
3) чему равна сумма первых трех членов арифметической прогрессии, если а1=7, а2=15 . S3-? (45)
4) в1=5, q=1/3. S2-? (6)
5) (вп)- бесконечная убывающая геом. прогрессия в1=4, q=1/2. найти её сумму (8)
6) определить по какому закону написаны пары строк и продолжить их
а) 1,3,7,15,…(31)
б)2,5,10,17,…(26)
7) найти х
20=20+18+16+14+…+х (-18)
IV. ЗАСЕДАНИЕ ПРОДОЛЖАЕТСЯ.
Проверим, как наши научные работники знают теоретический материал, т. Е. формулы. Отработаем понимание математической речи на слух.
У вас есть перфокарты, в окошечках которой вы должны будете вносить номер формулы, которую я зачитываю с доски.
1)аn = а1+d*(n-1)
2) вn = в1* qn-1
3) Sп = 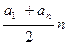 =
= 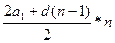
4) Sn = 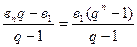 (q≠1)
(q≠1)
5)S = 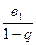 (/q/
(/q/ 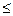 1)
1)
6) ап = ½(аn-1+ аn+1)
7) в2n = вn-1* вn+1
читаю названия этих формул :
1) свойство членов геометрической прогрессии (7)
2) сумма n- первых членов арифметической прогрессии (3)
3) сумма бесконечной геометрической прогрессии (/q/≤1) (5)
4) свойство членов арифметической прогрессии (6)
5) n-й член арифметической прогрессии (1)
6) сумма n-первых членов геометрической прогрессии (4)
7) n-й член геометрической прогрессии (2)
Проверим самостоятельно свои работы. Проверим ответы: 7356142
Оценочная система: «0» - 5
«1» - 4
«2»--3
поднимите сигнальные карточки у кого оценка 5,4,3,2
Попрошу заведующих кафедрами собрать перфокарты.
Мы выяснили, что наши сотрудники кафедр хорошо знают формулы и понимают математическую речь на слух. В повседневном общении это очень важное качество уметь воспринимать информацию на слух и быстро принимать решения.
V. Командировка
Научные сотрудники каждой кафедры ездили в творческие командировки, где должны были подобрать, подготовить задачи на изучаемую тему и составить сборник задач в соответствии с профилем кафедры. Заслушаем отчеты кафедр о проделанной работе.
1) Первой отчитывается кафедра «Истории математики»
Они составили сборник задач, в который вошло----- задач, составленных многими поколениями математиков, Познакомим вас с наиболее интересными из них.
( вывешивают рисунок)
1)Индийская легенда об изобретении шахмат (начало нашей эры)
Индийский царь Шерам позвал к себе изобретателя шахматной игры, своего подданного Сету, чтобы наградить его за остроумную выдумку. Сета попросил дать ему за 1клетку шахматной доски 1 зерно, за 2- 2, за 3-4, …. Обрадованный царь приказал выдать такую скромную награду. Смог ли царь наградить Сету как он просил?
В1=1,q=2.n=64.
1,2,22,23,…,263 – геометрическая прогрессия
S64= 264-1=8 446 744 073 709 551 615
18 квинтильонов 446 квадрильонов 744 триллиона 73 ,биллиона709 миллионов 551 тысяча 615.
Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз больше поверхности земли, а размер амбара, в который можно засыпать это зерно должны быть: высота- 4 м, ширина -10м., длина 30 000 000 км, что в 62 раза больше расстояния от земли до солнца. А вес этого зерна составит 184 млрд.467млн.440 тыс.737 тонн 95 кг. 516 г. пшеницы. Такое количество зерна необходимо выращивать 92 года.
2)Еще одна задача, которая была приведена в старинной арифметике Магницкого:
Некто продавал лошадь за 156 руб. Но покупатель раздумал приобретать лошадь, говоря: нет мне расчета покупать за эту цену лошадь, которая таких денег не стоит. Тогда продавец предложил другие условия:
Если по твоему, цена лошади высока, то купи только ее подковные гвозди, лошадь же тогда получишь бесплатно. Гвоздей в каждой подкове 6. за первый гвоздь дай мне всего ¼ копейки, за второй ½ коп., за третий-1 коп, и т. д Покупатель соблазненный низкой ценой и желая даром получить лошадь, принял условие, рассчитывая что за гвозди придется уплатить не более 10 руб. на сколько покупатель проторговался?
Составим последовательность: ¼,1/2,1,2,22,…,221- геометр. Прогрессия
q=2, а1=1/4, п=24 S= 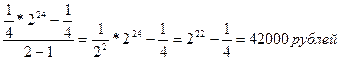
Я: ребята, в нашей жизни также встречаются игроки, предлагающие различные на первый взгляд заманчивые предложения игры. Но прежде, чем соблазниться подумайте, просчитайте, так ли уж выгодно предложение.
Спасибо кафедре «Истории математики» за интересные задачи. Сдайте свой сборник задач.
3)Приглашаем кафедру «Прикладной и вычислительной математики».
Члены кафедры подобрали задачи устного решения с непосредственным применением формул и задачи практического содержания.
1.Банк дает своим вкладчикам 15 % годовых. Чему станет, равен вклад 1000 тенге через 2 года?
Решение:
(вп) – геометрическая прогрессия
в1= 1000,q = 1,15 т. к. банк выдает саму эту сумму и + 15% годовых, в2= 1000*1,152=1322,5 (т).
2.Волшебный квадрат (выяснить свойство)
3.Заполнить пропуски
| … | ||
| … |
(26,14)
4.Найдите х:
20=20+18+16+14+…+х (-18)
5.Подставьте следующее число
1,3,7,15,… (31)
2,5,10,17,…(26)
6. Решить устно следующие задачи
1) ( ап)- арифметическая прогрессия, а1 = 4,d=3.а3-? (10)
2)(вп) -геометрическая прогрессия, в2=6, q =2, в1-? (3)
3) (ап) -арифметическая прогрессия а1=7, а2 = 15, S3_? (45)
4) (вп) -геометрическая прогрессия в1=5, q= 1/3, S2-? (6)
5) (вп) -бесконечная убывающая геометрическая прогрессия, в1=4, q= ½. Sп-? (8)
4)Отчет о творческой командировке кафедры «Исследования и анализа».
Они разработали сборник задач, содержащий ----задач. Члены кафедры предлагают решить задачу, которая связывает арифметическую и геометрическую прогрессии в своем условии.
VI. Спасибо всем кафедрам за большую работу по созданию сборников задач по теме геометрической и арифметической прогрессии.
Стук в дверь!
Пришел курьер, принес телеграмму следующего содержания:
«Уважаемые коллеги, у меня пропал важный документ. Прошу помочь его найти. На месте пропажи остались следы» профессор Прогрессио.
Итак, попрошу провести расследование заведующих кафедрами
Отдаю им следы с заданиями:
1) найти среднее арифметическое пятого и седьмого членов арифметической прогрессии, если а5= 33, а7=35
а6= 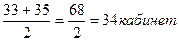
2) найти среднее геометрическое, если в1=1, в3= 9,
в2= 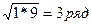
3) а1+а2+а3=3
а2+а3+а5=11
найти d, затем, разделив его значение на 2, найдете № стола.
а1-а5=-8
а1- (а1+4d) = -8
а1-а1-4d= -8
-4d=-8
d= 2
2/2=1 № стола
пока зав. Кафедрами расследуют дело о пропаже документа, выясним, как научные работники умеют быстро и четко находить верные ответы, решив следующие тесты.
