Производные сложной и обратной функции
В этом параграфе будет рассмотрен вопрос о дифференцируемости сложной функции
 , (4.1)
, (4.1)
где
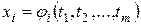 ,
,  . (4.2)
. (4.2)
Будет доказано, что при определенных условиях сложная функция
 (4.3)
(4.3)
по переменным 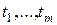 дифференцируема и ее частные производные выражаются через частные производные функции (4.1) и частные производные функций (4.2) по следующим формулам:
дифференцируема и ее частные производные выражаются через частные производные функции (4.1) и частные производные функций (4.2) по следующим формулам:
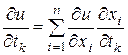 ,
, 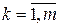 . (4.4)
. (4.4)
Теорема 4.1. Если функция (4.2) дифференцируема в точке 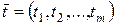 , а функция (4.1) дифференцируема в точке
, а функция (4.1) дифференцируема в точке 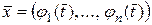 , то сложная функция (4.3) дифференцируема в точке
, то сложная функция (4.3) дифференцируема в точке 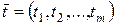 , причем ее частные производные в этой точке определяются формулой (4.4), где все частные производные
, причем ее частные производные в этой точке определяются формулой (4.4), где все частные производные 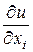 ,
,  вычисляются в точке
вычисляются в точке 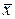 , а все частные производные
, а все частные производные  - в точке
- в точке 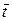 .
.
Доказательство. В силу дифференцируемости функции (4.1) в точке  ее полное приращение в этой точке представимо в виде
ее полное приращение в этой точке представимо в виде
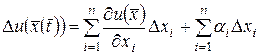 , (4.5)
, (4.5)
где
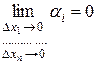 ,
,  . (4.6)
. (4.6)
Из дифференцируемости функции (4.2) в точке 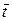 вытекает их непрерывность в этой точке, а по свойству непрерывности
вытекает их непрерывность в этой точке, а по свойству непрерывности
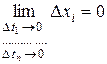 ,
,  . (4.7)
. (4.7)
Из (4.6) и (4.7) по свойству предела сложной функции следует
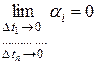 ,
,  . (4.8)
. (4.8)
В силу дифференцируемости функции (4.2) в точке 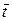 их полное приращение в этой точке можно представить в виде
их полное приращение в этой точке можно представить в виде
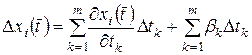 , (4.9)
, (4.9)
где 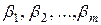 - бесконечно малые при
- бесконечно малые при 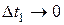 , …,
, …,  . После подстановки выражений (4.9) в правые части (4.5) получим
. После подстановки выражений (4.9) в правые части (4.5) получим
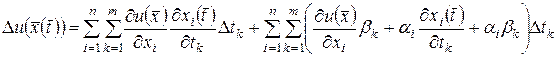
или
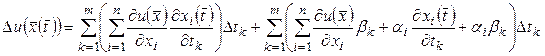 , (4.10)
, (4.10)
где в силу (4.8)  - бесконечно малые при
- бесконечно малые при 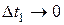 , …,
, …,  . По свойствам бесконечно малых сумма
. По свойствам бесконечно малых сумма

есть бесконечно малая при 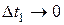 , …,
, …,  . Отсюда, согласно (4.10),
. Отсюда, согласно (4.10),
сложная функция (4.3) дифференцируема в точке 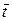 , причем ее частные производные в этой точке определяются формулами (4.4).
, причем ее частные производные в этой точке определяются формулами (4.4).
В частности, если аргументы функции (4.1) являются функциями одного переменного t: 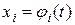 ,
,  , то производная сложной функции одного переменного t
, то производная сложной функции одного переменного t  определяется формулой
определяется формулой
 . (4.11)
. (4.11)
В случае сложной функции  , где
, где  , формула (4.11) принимает вид
, формула (4.11) принимает вид
 . (4.12)
. (4.12)
Займемся теперь вопросом о производной обратной функции одной переменной.
Определение 4.1. Функция  называется возрастающей (убывающей) на числовом промежутке Х, если для любых
называется возрастающей (убывающей) на числовом промежутке Х, если для любых 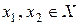 , удовлетворяющих условию
, удовлетворяющих условию 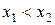 , справедливо неравенство
, справедливо неравенство
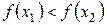 ,
, 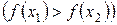 .
.
Возрастающая или убывающая функция называется монотонной. Пусть функция  задана на числовом промежутке Х и пусть множеством значений этой функции является числовой промежуток Y. Пусть далее каждому
задана на числовом промежутке Х и пусть множеством значений этой функции является числовой промежуток Y. Пусть далее каждому  соответствует только одно значение
соответствует только одно значение  , для которого
, для которого  . Тогда на числовом промежутке Y определяется функция
. Тогда на числовом промежутке Y определяется функция 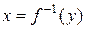 , сопоставляющая каждому
, сопоставляющая каждому  то значение
то значение  , для которого
, для которого  . Функция
. Функция 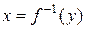 называется обратной для функции
называется обратной для функции  . Отметим, что если
. Отметим, что если 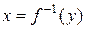 - обратная функция для
- обратная функция для  , то функция
, то функция  является обратной для
является обратной для 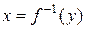 . Поэтому функции
. Поэтому функции  и
и 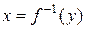 называются также взаимно обратными.
называются также взаимно обратными.
Теорема 4.2. Если функция  непрерывна и монотонна в некоторой окрестности точки х, то эта функция в соответствующей окрестности точки
непрерывна и монотонна в некоторой окрестности точки х, то эта функция в соответствующей окрестности точки  имеет непрерывную и монотонную обратную функцию
имеет непрерывную и монотонную обратную функцию 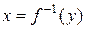 .
.
Доказательство этой теоремы приводится в [1].
Теорема 4.3. Пусть функция  монотонна и непрерывна в некоторой окрестности точки х и имеет в этой точке производную
монотонна и непрерывна в некоторой окрестности точки х и имеет в этой точке производную 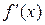 , отличную от нуля. Тогда обратная функция
, отличную от нуля. Тогда обратная функция 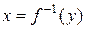 в точке
в точке  имеет производную
имеет производную  , определяемую формулой
, определяемую формулой
 . (4.13)
. (4.13)
Доказательство. Согласно теореме 4.2 при условиях теоремы 4.3 функция  в окрестности точки
в окрестности точки  имеет монотонную и непрерывную обратную функцию
имеет монотонную и непрерывную обратную функцию 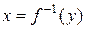 . Придадим значению y произвольное, отличное от нуля приращение
. Придадим значению y произвольное, отличное от нуля приращение 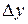 . Этому приращению соответствует приращение
. Этому приращению соответствует приращение 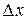 обратной функции, причем в силу монотонности функции
обратной функции, причем в силу монотонности функции 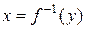 приращение
приращение  (иначе разным значениям аргумента функции
(иначе разным значениям аргумента функции 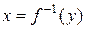 будут соответствовать одинаковые значения функции, что противоречит условию монотонности обратной функции). Поэтому мы вправе записать следующее тождество
будут соответствовать одинаковые значения функции, что противоречит условию монотонности обратной функции). Поэтому мы вправе записать следующее тождество
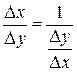 . (4.14)
. (4.14)
Пусть теперь в равенстве (4.14)  . Тогда в силу непрерывности обратной функции в точке y будет
. Тогда в силу непрерывности обратной функции в точке y будет  . Но при
. Но при  дробь
дробь  в силу существования ненулевой производной функции
в силу существования ненулевой производной функции  имеет предельное значение
имеет предельное значение  . Следовательно, правая часть (4.14) имеет при
. Следовательно, правая часть (4.14) имеет при  предельное значение, равное
предельное значение, равное  . Но тогда и левая часть (4.14) при
. Но тогда и левая часть (4.14) при  имеет предельное значение, равное
имеет предельное значение, равное  . Отсюда вытекает формула (4.13) или, короче,
. Отсюда вытекает формула (4.13) или, короче,
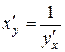 . (4.15)
. (4.15)
Доказательство теоремы имеет простой геометрический смысл. Рассмотрим в окрестности точки х график функции  (или все равно что график обратной функции
(или все равно что график обратной функции 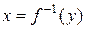 ). Производная
). Производная 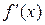 равна тангенсу угла наклона
равна тангенсу угла наклона 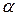 касательной в точке
касательной в точке  к оси ОХ. Производная
к оси ОХ. Производная  равна тангенсу угла наклона
равна тангенсу угла наклона 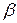 касательной в этой же точке М к оси OY. Поскольку
касательной в этой же точке М к оси OY. Поскольку 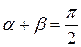 , то условие (4.15) будет иметь вид
, то условие (4.15) будет иметь вид 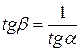 (см. рис. 4.1).
(см. рис. 4.1).

Рис. 4.1
