Задачи для самостоятельного решения

Решите системы линейных уравнений АХ = В методом Гаусса.

№	А	В	Х (ответы)
1.	,	,	.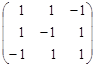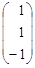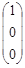
2.	,	,	.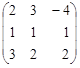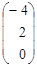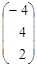
3.	,	,	.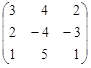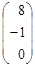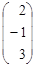
4.	,	,	.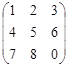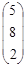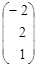
5.	,	,	.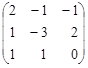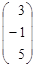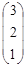
6.	,	,	.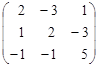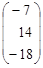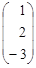

Матрицы. Основные понятия

В предыдущем разделе мы изучили некоторые операции с матрицами, рассматривая только квадратную матрицу третьего порядка и матрицу-столбец. В общем случае матрицей размерности m´n называется прямоугольная таблица чисел, содержащая m строк и n столбцов:

А_(m´n) = .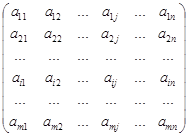

Числа 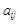называются элементами матрицы, первый индекс 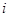– номер строки, второй индекс j – номер столбца, на пересечении которых находится элемент .

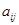Пример 1.5

;

;

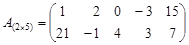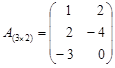А_(1´4) = (–1 2 5 7).

Во втором разделе была рассмотрена матрица-столбец. Матрица 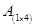называется матрицей-строкой.

Если m = n, то матрица

A_(n´n) =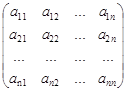

называется квадратной матрицей n–ого порядка.

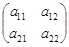– квадратная матрица второго порядка,

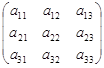– квадратная матрица третьего порядка.

В квадратной матрице диагональ, образованная элементами a₁₁, a₂₂, a₃₃, …., a_{n n} , называется главной диагональю матрицы.

Квадратная матрица называется диагональной, если все ее элементы, не лежащие на главной диагонали, равны нулю:

.

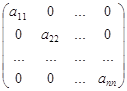Диагональная матрица, все диагональные элементы которой равны единице, называется единичной матрицей:

E = .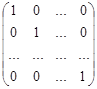

(1.8)

Большой буквой 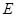в дальнейшем будем обозначать единичную матрицу.

Линейные операции над матрицами

Матрицы можно складывать между собой и умножать на числа. Такие действия называются линейными операциями над матрицами.

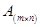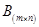1. Суммой двух матриц и одинаковой размерности m´n называется матрица 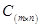такой же размерности, элементы которой равны суммам соответствующих элементов матриц A и В. Из этого определения следует, что складывать можно только матрицы одинаковой размерности, т.е. матрицы с одинаковым количеством строк и столбцов.

Пример 1.6

1) А+В = ;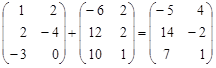

2) матрицы

А = 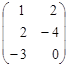и В =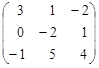

сложить нельзя, так как они имеют разное количество столбцов.

2. Произведением матрицы 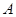на число l называется матрица lА, каждый элемент которой равен произведению соответствующего элемента матрицы А на число l.

Пример 1.7

3× =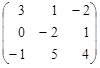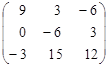

(1.8)

3. Две матрицы A и 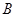одинаковой размерности m´n считаются равными, если равны их соответствующие элементы a_ik = b_ik .

Умножение матриц

В третьем разделе было изучено правило (1.6) умножения квадратной матрицы третьего порядка на столбец. Рассмотрим теперь умножение матрицы 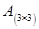на матрицу 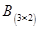. Подчеркнем, что число столбцовматрицы А, равно числу строкматрицы В. Отличие произведения А_(3´3) × В_(3´2) от формулы (1.6), рассмотренной в третьем разделе, заключается только в том, что матрица В имеет теперь два столбца, поэтому матрица D = А_(3´3)× В_(3´2) тоже имеет два столбца, т.е. столько же столбцов, сколько их в матрице В. При этом первый столбец матрицы D равен произведению матрицы А на первый столбец матрицы В, а второй столбец матрицы D – это произведение матрицы А на второй столбец матрицы В:

А_(3´3)× В_(3´2) = =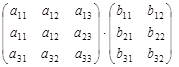

= .

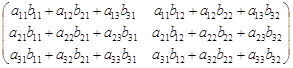(1.9)

Посмотрим, как изменится формула умножения матриц (1.9), если в матрице А добавить еще одну строку:

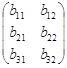
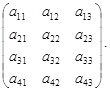
А_(4´3)× В_(3´2)= =

= .

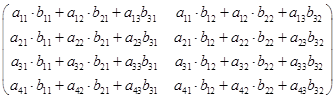(1.10)

Как видим, добавление строки в матрицу А приводит к добавлению строки в матрицу D = A×B, т.е. можно записать

.

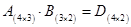(1.11)

Если в матрице 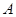прибавить один столбец, то произведение такой матрицы A_(3´4) на матрицу B_(3´2) по рассмотренным выше правилам найти невозможно. В этом случае говорят, что произведение матриц не существует. Матрицу A_(3´4), имеющую четыре столбца, можно умножить только на матрицу, имеющую четыре строки, например на матрицу B_(4´2):

= .

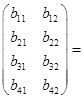
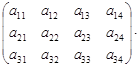
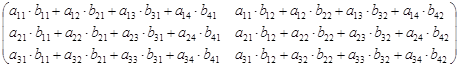Таким образом, .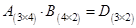

Из примера можно сделать следующие основные выводы об умножении матриц:

1) произведением некоторой матрицы А_{(m ´ k)} на матрицу В_{(k ´ n)} является матрица D_{(m ´ n)}= А_{(m ´ k)} × В_{(k ´ n)} . Число строк матрицы D равно числу строк матрицы А, а число столбцов матрицы D равно числу столбцов матрицы В;

2) если число столбцов матрицы А (первого сомножителя в произведении) не равно числу строк матрицы В (второго сомножителя), то произведение таких матриц не существует;

3) каждый столбец матрицы D_{(m ´ n)}= А_{(m ´ k)} × В_{(k ´ n)} строится как произведение матрицы А на соответствующий столбец матрицы В.

Из сказанного следует, что операция умножения матриц не обладает свойством коммутативности (перестановочности), т.е. в общем случае АВ¹ВА. Более того, при существовании произведения АВ произведение ВА может и не существовать.

Приведем еще несколько примеров умножения матриц.

Пример 1.8

Легко показать, что АЕ = ЕА = А, где А – квадратная матрица произвольного порядка, Е – единичная матрица того же порядка (см. определение и формулу (1.8)), что и матрица А. Действительно, пусть А – квадратная матрица третьего порядка, тогда

АЕ = =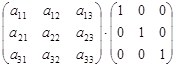

= =

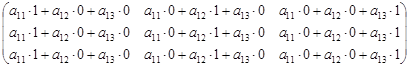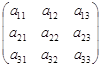= = А.

Равенство ЕА = А доказывается аналогично.

Пример 1.9

.

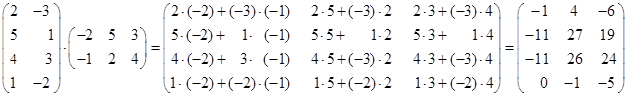Пример 1.10

.

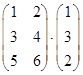В этом случае произведение не существует, так как число столбцов матрицы А (равно 2) не равно числу строк матрицы В (равно 3).

Пример 1.11

А= 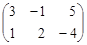, В = .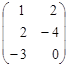

Найти АВ и ВА.

Решение

АВ = × =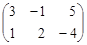

= = ;

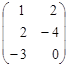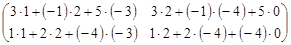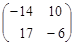ВА = × =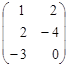

= = .

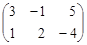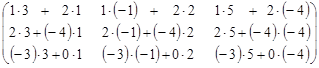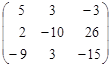Как видим, в этом случае существуют оба произведения АВ и ВА, однако они не равны между собой.

Пример 1.12

× =

= = .

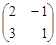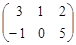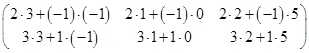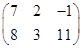Пример 1.13

× =

= =

= .
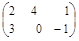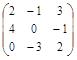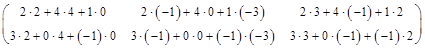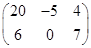