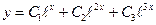Понятие об устойчивости и асимптотической устойчивости решения диф.уравнения первого порядка, разрешенного относительно производной

При изучении какого-либо явления, описываемого диф.уравнением, начальные условия для которого определяются приборами с различными погрешностями, малые отклонения в начальных данных могут привести к большим отклонениям при больших t. Поэтому возникает задача определить насколько решение отличается от изучаемого (истинного) при всех нужных t.

Теорема: Если правая часть диф.уравнения 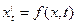непрерывна по совокупности аргументов и имеет ограниченную частную производную по x в некоторой окрестности точки 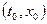, то тогда решение, проходящее через эту точку, непрерывно зависит от начальных данных.

(Без док-ва)

Рассмотрим уравнение 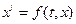, функция f(t,x) определена и непрерывна для 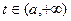, а – некоторое число, х берется из некоторой области и имеет ограниченную частную производную .

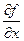Пусть функция 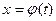есть решение данного уравнения, удовлетворяющее начальному условию 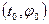. Еще одна функция x=x(t) есть решение того же уравнения, удовлетворяющее другому начальному условию, а именно 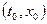. Предполагается также, что решения x(t)и 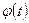определены при .

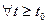Опр.:Решение 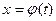наз-ся устойчивым по Ляпунову при 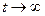, если для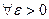 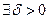и такое, что из условия .

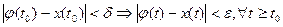Это значит, что решения близкие по начальным данным решению 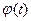остаются близкими к этому решению .

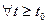Если хотя бы одно из решений x(t) не удовлетворяет такому условию, то решение 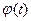наз-ся неустойчивым.

Опр.: Решение 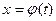наз-ся асимптотически устойчивым, если:

1. оно устойчиво;

2. .

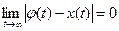Очевидно, что из асимптотической устойчивости следует устойчивость, а в обратную сторону не выполняется.

ПримерХХ:Исследовать на устойчивость тривиальное решение уравнения: x’=0

X=C, x=0, j(t)=0 – тривиальное решение. , .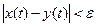

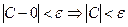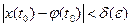
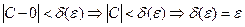
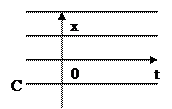решение j(t)=0 не является асимптотически устойчивым.

Пример 1:Исследовать на устойчивость решение уравнения: x 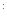=-2tx, x(0)=0.

(Ответ: при t 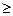0 асимптотически устойчиво).

Пример 2:x 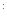=2t, x(0)=0

(Ответ: устойчиво не асимптотически).

Пример 3:tx 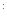=x, x(1)=0/

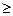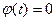(Ответ: при t 1 неустойчиво)

Продолжение 31

Фаз.портрет – “Звездный устойчивый узел”, не прямые – а лучи.

Вывод:очевидно, что все траектории системы приближаются к неподвижной точке (0;0), значит, все интегральные кривые будут приближаться к прямой 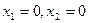. Таким образом, данная прямая является устойчивым, даже асимптотическим, решением системы.

2)

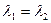
Тип фазового портрета зависит от элементарных делителей матрицы коэфф-ов. Если матрица коэф-ов невырожденная, то в случае, когда имеется один непростой делитель получается один вырожденный узел:

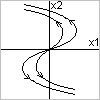
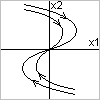
Если 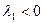- устойчивый 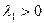- неустойчивый

Если матрица коэф-ов имеет два простых элементарных делителя,

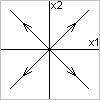
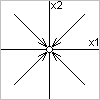
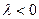- устойчивость 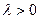- неустойчивость

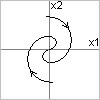3) 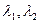- комплексно-сопряженные,т.е.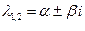

Если 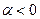- устойчивый фокус (закручивающиеся спирали)

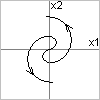
Если 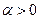- неустойчивый фокус (раскручивающиеся спирали)

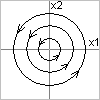
Если 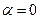, то фазовый портрет наз-ся центром(он устойчивый, но не асимптотически)

Для системы n-уравнений 1-го порядка с постоянными коэф-ми справедливы следующие предложения:

· Если все корни характер-го уравнения имеют отрицательную действительную часть, то всерешения системы - устойчивы;

· Если хотя бы один корень харак-го уравнения имеет положительную действительную часть, то все решения системы - неустойчивы;

· Если харак-е уравнение имеет простые корни с нулевой действит-ой частью, а остальные корни, если они есть, имеют отриц-ую действит-ую часть, то все решения системы - устойчивы, но не асимптотически.

Продолжение 27а

Пример:Решить систему: 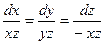(2)

Решение:,

(Система (2) записана в симметрической форме). Первые две дроби образуют интегрируемую комбинацию. Сокращая равенство 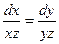на 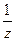и интегрируя, получаем первый интеграл

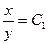(3)

Чтобы найти вторую интегрируемую комбинацию, воспользуемся следующим свойством равных дробей: если 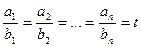, то при любых 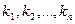имеем: 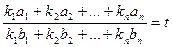. Пользуясь этим свойством, получаем из (2): 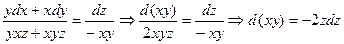. Следовательно,

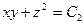(4)

Очевидно, первый интеграл (3) и первый интеграл (4) независимы. Система решена.

Вместо того чтобы искать вторую интегрируемую комбинацию, можно, воспользовавшись знанием первого интеграла (3),исключить из системы (2) одно из неизвестных, например x. Из (3) имеем 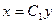. Подставляя во второе из уравнений (2), получаем: 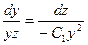. Отсюда: 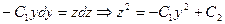. Подставляя сюда выражение для 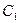из формулы (3), находим еще один первый интеграл: .

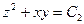Введем в рассмотрение линейный диф.оператор: 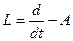. Тогда система записывается в краткой форме: L(x)=F. Если матрица F – нулевая, то система наз-ся однородной и записывается L(x)=0.

Теорема 2:Если вектор x(t) является решением лин. однородной системы, то произведение этого вектора на любую const C тоже есть решение этой системы.

Теорема 3:Если векторы 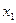и 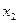являются решениями однородной системы, тогда и их сумма 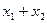является решением данной системы.

Следствие:решением однородной системы является любая линейная комбинация ее решений с постоянными коэф-ми.

Теорема 4:Если 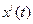есть решение линейной неоднородной системы, а - решение соответствующей однородной системы, то сумма 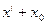есть решение неоднородной системы.

Решение неоднородной системы 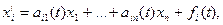i=1,…,n можно найти методом вариации постоянных, если известно общее решение однородной системы с теми же коэф-ми 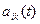. Для этого в формуле общего решения однородной системы надо заменить произвольные постоянные 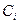на неизвестные функции 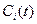. Полученные выражения для 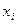надо подставить в данную неоднородную систему, и из этой системы найти .

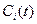Продолжение 29

Замечание:Пусть правая часть неоднородного линейного уравнения представляет собой формулу двух функций: .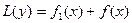

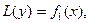Пусть - есть частное решение. а 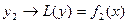. Следовательно: сумма 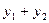является решением этого данного уравнения.

Определитель Вронского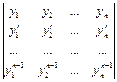

Пример: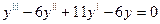

Общее решение данного уравнения записывается в виде: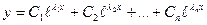

Запишем характеристическое уравнение: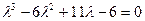

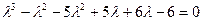
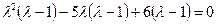
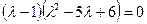
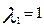
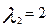
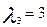
Решение будет иметь вид: