Дифференциал сложной функции

Дифференциал сложной функции z = z(x; y), где x = x(u; v), y = y(u; v), можно получить, если в формуле дифференциала

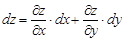
заменить 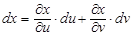и

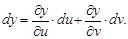
В результате подстановки и перегруппировки членов при du и dv приходим к формуле

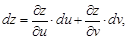
показывающей, что форма (вид) дифференциала не зависит от того, являются ли x и y независимыми переменными или функциями других независимых переменных. Это свойство называется инвариантностью формы первого дифференциала.

Неявная функция одной переменной

Функция называется неявной функцией, если она определяется уравнением 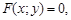неразрешенным относительно y.

Это значит, что при каждом значении x₀, при котором неявная функция определена, она принимает единственное значение y₀ так, что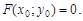

Теорема.Если F(x; y) – дифференцируемая функцияпеременных x и y в некоторой области D и 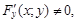то уравнение F(x; y) = 0 определяет однозначно неявную функцию y(x), также дифференцируемую, и ее производная находится поформуле

В частности,

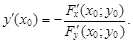
Неявная функция двух переменных

Функция z = z(x; y) называется неявной функцией переменных x и y, если она определяется уравнением F(x; y; z) = 0, неразрешенным относительно z.

Теорема. Если функция F(x; y; z) дифференцируема по переменным x, y, z в некоторой пространственной области D и 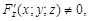то уравнение F(x; y; z) = 0 определяет однозначную неявную функцию z(x; y), также дифференцируемую, и имеет место

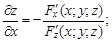
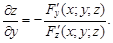
Пример 18.Найти частные производные функции где u = 2x + 3y; v = xy.

Решение

Имеем

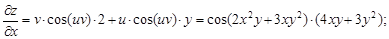
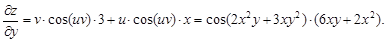
Пример 19.Найти полную производную функции 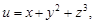где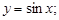

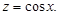
Решение

Имеем

Пример 20.Найти производную функции y, заданной неявно урав-
нением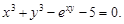

Решение

Согласно формуле имеем

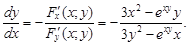
Пример 21.Найти частные производные функции z, заданной неявно уравнением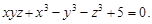

Решение

Воспользуемся формулами. Получим

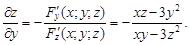
Тест 13. Частная производная 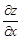функции z, заданной неявно уравнением 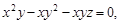равна:

1)

2)

3)

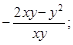
4)

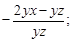
5)

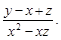
Экстремум функции двух переменных

Понятия максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной.

Пусть функция z = f(x; y) определена в некоторой области D, точка M₀(x₀; y₀) Î D.

Функция z = f(x; y) имеет локальный максимум (минимум) в точке M₀(x₀; y₀), если неравенство

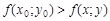
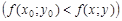
имеет место во всех точках M(x; y), достаточно близких к M₀(x₀; y₀), но отличных от нее.

Максимум или минимум функции называется экстремумом, а точки минимума и максимума функции называются точками локального экстремума.

В силу определения, точка локального экстремума функции лежит внутри области определения функции.

В области D функция может иметь несколько экстремумов или не иметь ни одного.