Виды матриц. ранг матрицы

Любая таблица, состоящая из чисел, записанных в определенном порядке, содержащая m строк и n столбцов, называется матрицей размерности m×n; число a_ij – элемент матрицы.

Способы задания матриц:

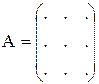
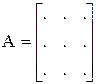
А_1×n – матрица-строка

А_1×m – матрица-столбец

Матрица, все элементы которой – нули – нулевая матрица.

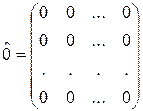
Если m≠n, матрица – прямоугольная;

если m>n, матрица – укороченная;

если m<n, матрица – удлиненная;

если m=n, матрица – квадратная.

|A| – определитель матрицы.

Размерность квадратной матрицы называется ее порядком.

Если определитель квадратной матрицы ≠ 0, то такая матрица – невырожденная (неособенная);

Если определитель квадратной матрицы = 0, то такая матрица – вырожденная (особенная).

Квадратная матрица вида

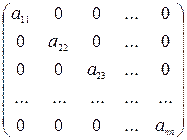
где а₁₁, а₂₂, … , а_nn – элементы , распределенные по главной диагонали, называется диагональной матрицей.

Диагональная матрица, все элементы которой по главной диагонали равны 1, называется единичной матрицей (E_n).

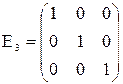
Любое число можно считать матрицей первого порядка.

Если у матрицы переставить местами столбцы со строками, то такая операция называется транспонированием матрицы.

А^т – транспонированная матрица.

|А| = |А^т| (если А – квадратная)

(А^т)^т = А

Квадратная матрица называется симметрической, если А = А^т , т.е. a_ij = a_ji для любых i и j.

Элементы симметрической матрицы, расположенные симметрично относительно главной диагонали, равны.

Квадратная матрица называется ортогональной, если ее столбцы образуют ортонормированную систему векторов.

Рассмотрим матрицу А = (a_ij), i = 1, m ; j = 1, n.

Из этой матрицы можно образовать квадратные матрицы. Определители таких матриц называют минорами данной матрицы. Порядок этих миноров не превышает min(m, n).

Пример:

Для матрицы А_5×4 наибольший порядок минора ≤ 4.

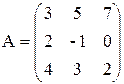– квадратная матрица 3 порядка:

9 миноров 1 порядка;

9 миноров 2 порядка;

1 минор 3 порядка;

Рангом матрицы называется максимальный порядок миноров матрицы, отличных от нуля.

Если ранг матрицы r(A) = r, то по крайней мере один из миноров этой матрицы порядка r отличен от нуля, и все миноры более высоки порядков (если они существуют) равны 0.

Ранг матрицы можно вычислить следующими методами:

1) Метод окаймляющих миноров

2) Метод, основанный на элементарных преобразованиях матрицы

Рассмотрим первый метод.

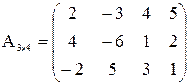
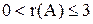
r(A) может принимать значения 1, 2, 3.

Выбираем минор первого порядка:

М₁ = -3

Составляем М₂, окаймляющий М₁ ≠ 0

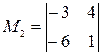= 21 ≠ 0

=> r(A) = 2 или 3.

Составляем М₃, окаймляющий М₂ 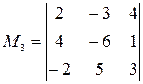≠ 0

≠ 0

=> r(A) = 3

Базисным минором матрицы называется минор, не равный нулю, порядок которого равен рангу данной матрицы.

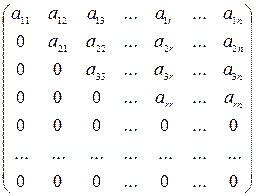
называется трапецеидальной.

Каждую матрицу с помощью элементарных преобразований можно превратить в трапецеидальную. Ранг трапецеидальной матрицы равен числу ненулевых строк.

Т.к. элементарные преобразования матрицы не меняют ее ранга, то для отыскания ранга любой матрицы нужно:

1) Преобразовать данную матрицу в трапецеидальную;

2) Подсчитать число ненулевых строк

3) Ранг трапецеидальной матрицы будет равен рангу данной матрицы.