Примеры решения практических задач
Тема:"Линейные действия над матрицами"
П р и м е р 1.1.Найти матрицу А + В, если
, 
.
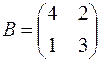Решение.Чтобы выполнить линейную операцию сложения над матрицами необходимо сложить одноименные элементы этих матриц, т. е. 
П р и м е р 1.2.Найти матрицу А − В, если
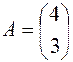и 
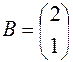
Решение.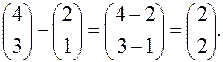
П р и м е р 1.3. Найти матрицу 5×А, если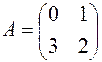 
.
Решение. Чтобы умножить матрицу на число необходимо умножить все элементы матрицы на это число, т. е.
П р и м е р 1.4. Найти А∙В, если
и .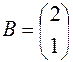
Решение.
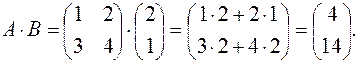
Тема "Определители второго и третьего порядков"
П р и м е р 1.5.Вычислить определитель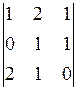 
.
Решение. 
или
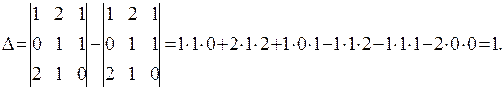
П р и м е р 1.6. Найти алгебраическое дополнение элемента а21 определителя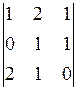
Решение.
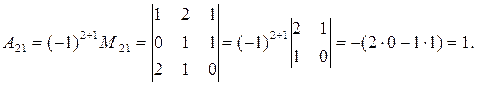
Тема "Свойства определителей"
П р и м е р 1.7. Вычислить определитель, разложив его по элементам какой − либо строки или столбца:
.
Решение. Разложим данный определитель по второму столбцу:
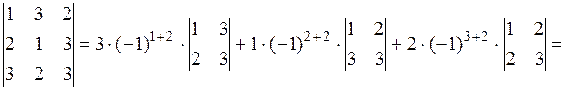
П р и м е р 1.8. Вычислить определитель 
, используя свойство 3.
Решение. Так как элементы первого столбца имеют общий множитель 2, то, по свойству 3, получаем:
П р и м е р 1.9.Проверить свойство 4 на примере определителя
.
Решение. В данном определителе третий столбец с нулевыми элементами, следовательно, он равен нулю. Применим формулу Саррюса и докажем что это действительно так.
П р и м е р 1.10. Проверить свойство 5 для определителя 
Решение. В данном определителе поменяем местами первую и вторую строки и вычислим оба определителя по формуле Саррюса.
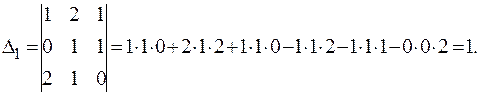
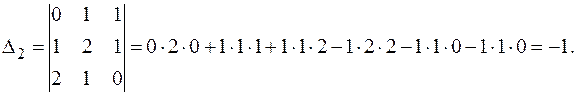
Таким образом получили, что Δ1 = Δ2.
П р и м е р 1.11. Вычислить определитель 
Решение. Так как в данном определителе соответствующие элементы второй и третьей строк равны, то, согласно свойству 6, он равен нулю. Покажем это, вычислив определитель:
П р и м е р 1.12. Вычислить определитель 
, восползовавшись свойством 7.
Решение. Сначала вычислим данный определитель по формуле Саррюса.
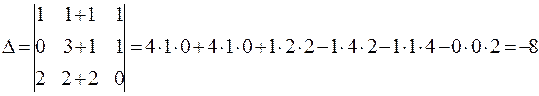
В определителе представим один из столбцов, например второй, в виде суммы элементов и применим свойство 7, т. е. определитель распишем в виде суммы двух определителей и вычислим их по отдельности.
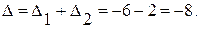
П р и м е р 1.13. Вычислить определитель 
и проверить
свойство 8.
Решение. Вычислим определитель по формуле Саррюса.
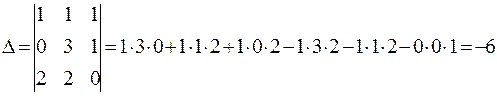
Теперь к элементам второго столбца прибавим соответствующие элементы первого столбца, умноженные на два, и вычислим полученный определитель.
Тема "Обратная матрица. Матричные уравнения"
П р и м е р 1.14.Найти обратную матрицу по отношению к матрице
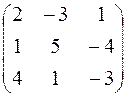
Решение. Вычислим определитель данной матрицы:
Найдем алгебраические дополнения всех элементов данной матрицы:
; 
;
; 
;
; 
; 
; 
;
.
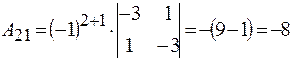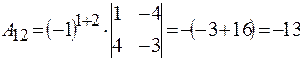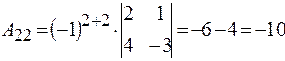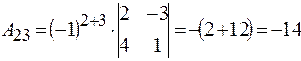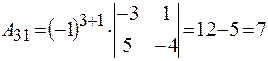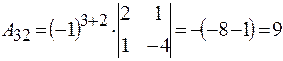Составим обратную матрицу, подставив найденные значения в формулу (1.1):
.
П р и м е р 1.15. Решить матричное уравнение
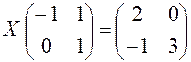
Решение. Найдем матрицу А-1 для матрицы А =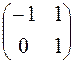 
.
Имеем Х∙А = В, тогда Х = В∙А– 1, где А = 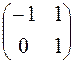, В =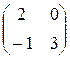 
Для этого вычислим определитель матрицы А:
и найдём алгебраические дополнения всех элементов этой матрицы:
; 
;
; 
;
.
.
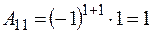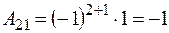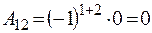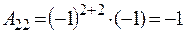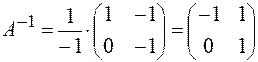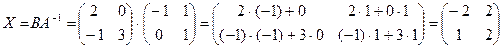Проверка: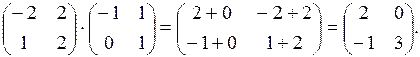 
Тема "Системы линейных алгебраических уравнений"
П р и м е р 1.16.Решить систему алгебраических уравнений с помощью обратной матрицы:
Решение. Запишем систему линейных неоднородных уравнений в виде матричного уравнения:
.
Найдем обратную матрицу по отношению к матрице 
.
Вычислим определитель этой матрицы.
.
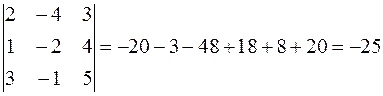Найдем алгебраические дополнения элементов матрицы системы:
; 
;
; 
;
; 
;
; 
;
.
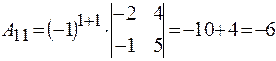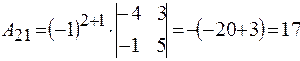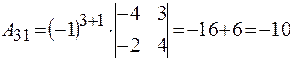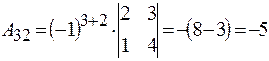Тогда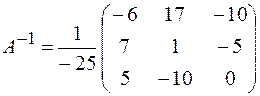 
Умножим обратную матрицу слева на матрицу – столбец свободных членов и получим искомую матрицу Х:
Следовательно, х = - 1, у = 0, z = 1.
Проверка:
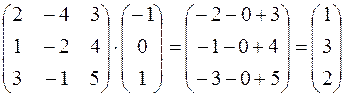верно.
СПИСОК ЛИТЕРАТУРЫ
1.Болотина Н.А Руденок И.П., Харитонова Л.П. Высшая математика[Электронный ресурс]:учебно-практическое пособие. – 2-е изд., перераб. И доп./М-во образования и науки Росс. Федерации, Волгогр. Гос. Архит.-строит. Ун-т.- Электрон. Текстовые данные (3,6Мб).- Волгоград: ВолгГАСУ, 2012.- Официальный сайт Волгоградского государственного архитектурно-строительного университета. Режим доступа: http//www/vgasu.ru/publishing/on-line/.
2.Шипачев В.С. Высшая математика. М.: Высш. шк., 2005. — 479 с.
3.Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука. Главная редакция физико-математической лит-ры, 1985. – Т 1, 2.
4.Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа: Учебник для вузов. — СПб.: Изд-во «Лань», 2005. — 736 с.
5.Данко П.Е. Высшая математика в упражнениях и задачах (с решениями): [учеб. пособие для вузов] : в 2 ч. Ч. 1,2 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 6-е изд. - М. : ОНИКС 21 век : Мир и Образование, 2006. - 303, [1]с.
6.Высшая математика: краткий теоретический курс с примерами решения задач: Учебно-методический комплекс (учебное пособие) (авторы: Руденок И.П., Харитонова Л.П., Вишнякова Е.Г., Заикина Т.Б.). Волгоград, ВолгГАСУ, 2007.
Вопросы для подготовки (1 семестр ускор.).
Линейная алгебра
1. Понятие матрицы, виды матриц, основные определения.
2. Действия над матрицами. Основные свойства.
3. Определители. Миноры и алгебраические дополнения. Вычисление определителей второго, третьего и высших порядков.
4. Основные свойства определителей.
5. Обратная матрица и ее нахождение.
6. Элементарные преобразования матриц. Ранг матрицы и его нахождение.
7. Системы линейных алгебраических уравнений (СЛАУ), основные определения.
8. Исследование СЛАУ на совместность. Теорема Кронекера — Капелли.
9. Решение невырожденных линейных систем по формулам Крамера и методом обратной матрицы.
10. Решение СЛАУ методом Гаусса.
11. Исследование и решение систем линейных однородных уравнений.
12. Геометрические векторы, основные определения.
13. Линейные операции над векторами, свойства линейных операций.
14. Прямоугольная декартова система координат. Координаты вектора. Разложение вектора по ортам координатных осей.
15. Действия над векторами в координатной форме.
16. Скалярное, векторное, смешанное произведения векторов, их свойства и приложения.
17. Векторные пространства. Линейные операции над векторами.
18. Базис n - мерного пространства.
Аналитическая геометрия
19. Прямая на плоскости, различные виды уравнений, взаимное расположение.
20. Эллипс, гипербола, парабола. Их свойства, уравнения и построение.
21. Плоскость. Основные уравнения. Частные случаи.
22. Прямая в пространстве. Основные уравнения. Частные случаи.
23. Задачи на взаимное расположение прямых и плоскостей в пространстве.
Дифференциальное исчисление функции одной переменной
24. Множества. Операции над множествами.
25. Функции одной переменной. Область определения, способы задания и основные свойства.
26. Понятие обратной, сложной, элементарной функций.
27. Понятие предела переменной величины, предела функции в точке. Односторонние пределы.
28. Бесконечно малые и бесконечно большие величины, их свойства и связь между ними.
29. Основные теоремы о пределах. Признаки существования предела.
30. Первый и второй замечательные пределы.
31. Непрерывность функции в точке и на отрезке.
32. Точки разрыва функций и их классификация.
33. Понятие производной и ее различные толкования.
34. Дифференцируемость функции в точке и на отрезке. Связь между дифференцируемостью и непрерывностью функции в точке.
35. Простейшие правила вычисления производных.
36. Производные сложной и обратной функций.
37. Производные основных элементарных функций.
38. Дифференцирование неявных и параметрически заданных функций.
39. Логарифмическое дифференцирование.
40. Дифференциал, его геометрический смысл, применение к приближенным вычислениям.
41. Производные и дифференциалы высших порядков.
42. Теоремы о дифференцируемых функциях (Ферма, Ролля, Лагранжа, Коши). Правило Лопиталя.
43. Исследование функций методами дифференциального исчисления (монотонность, экстремумы, точки перегиба, асимптоты).
44. Задача о наибольшем и наименьшем значениях функции на отрезке.
Дифференциальное исчисление функции нескольких переменных
45. Понятие функции нескольких переменных. Область определения, способы задания. Предел, непрерывность.
46. Частные производные. Геометрический смысл частных производных функций двух переменных.
47. Дифференцируемость в точке, полный и частные дифференциалы. Применение полного дифференциала к приближенным вычислениям.
48. Производные и дифференциалы высших порядков.
49. Дифференцирование неявных функций.
50. Касательная плоскость и нормаль к поверхности.
51. Экстремумы. Необходимые и достаточные условия экстремума.
52. Производная по направлению, градиент, связь между ними.
Интегральное исчисление функции одной переменной
53. Определение понятий первообразной и неопределенного интеграла. Основная теорема о первообразных.
54. Теорема существования первообразной и неопределенного интеграла.
55. Таблица основных интегралов.
56. Свойства неопределенных интегралов.
57. Основные методы интегрирования. Метод замены переменной. Метод интегрирования по частям.
58. Интегрирование выражений, содержащих квадратный трехчлен.
59. Разложение рациональной дроби на простейшие и их интегрирование. Интегрирование рациональных дробей.
60. Интегрирование простейших иррациональных функций.
61. Интегрирование тригонометрических функций с помощью тригонометрических подстановок. Универсальная тригонометрическая подстановка.
62. Определенный интеграл как предел интегральной суммы.
63. Теорема существования определенного интеграла.
64. Свойства определенного интеграла. Теорема о среднем.
65. Формула Ньютона- Лейбница.
66. Метод замены переменной в определенном интеграле.
67. Метод интегрирования по частям в определенном интеграле.
68. Вычисление площади криволинейной трапеции в прямоугольных координатах.
69. Вычисление площади криволинейного сектора в полярных координатах.
70. Вычисление объема тела по площадям параллельных сечений.
71. Объем тела вращения.
72. Длина дуги плоской кривой в прямоугольных и полярных координатах.
73. Несобственные интегралы с бесконечными пределами интегрирования и от неограниченных функций. Признак сходимости несобственных интегралов.