Важнейшие замкнутые классы
1) Класс функций, сохраняющих ноль. Обозначение: Т0.
Т0={f(x1,x2,…,xn)ÎP2: f(0,0,…,0)=0}, таким образом, этот класс состоит из тех функций алгебры логики, которые на наборе, состоящем из одних нулей, имеют значение ноль. Или, что то же самое, в верхней строке таблицы истинности значение этих функций равно нулю. И поскольку, ровно половина всех функций в верхней строке равны нулю, то число функций от n переменных, относящихся к классу Т0, равно 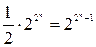 . Из элементарных функций к этому классу относятся следующие: 0, х, &, Ú, Å. А такие, как 1,
. Из элементарных функций к этому классу относятся следующие: 0, х, &, Ú, Å. А такие, как 1, 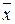 , º, ® не принадлежат классу Т0.
, º, ® не принадлежат классу Т0.
2) Класс функций, сохраняющих единицу. Обозначение: Т1.
Т1={f(x1,x2,…,xn)ÎP2: f(1,1,…,1)=1}, таким образом, этот класс состоит из тех функций алгебры логики, которые на наборе, состоящем из одних единиц, имеют значение 1. Или, что то же самое, в нижней строке таблицы истинности значение этих функций равно единице. И, поскольку, ровно половина всех функций в нижней строке равны единице, то число функций от n переменных, относящихся к классу Т1, равно 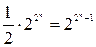 . Из элементарных функций к этому классу относятся следующие: 1, х, &, Ú, º, ®. А такие, как 0,
. Из элементарных функций к этому классу относятся следующие: 1, х, &, Ú, º, ®. А такие, как 0, 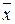 , Å не принадлежат классу Т1.
, Å не принадлежат классу Т1.
3) Класс самодвойственных функций. Обозначение: S.
S={f(x1,x2,…,xn)ÎP2: f(x1,x2,…,xn)=f *(x1,x2,…,xn) }, таким образом, этот класс состоит из тех функций алгебры логики, которые совпадают с двойственными к ним. Заметим, что такие функции на противоположных наборах принимают противоположные значения, т.к. f(x1,x2,…,xn)=  . Таблицы истинности этих функций имеют зеркальную симметрию верхней половины строк таблицы и инвертированной нижней половины строк относительно середины всех строк таблицы. Тем самым, самодвойственные функции полностью определяются своими значениями на первой половине строк таблицы. Число таких строк для функций от n переменных равно
. Таблицы истинности этих функций имеют зеркальную симметрию верхней половины строк таблицы и инвертированной нижней половины строк относительно середины всех строк таблицы. Тем самым, самодвойственные функции полностью определяются своими значениями на первой половине строк таблицы. Число таких строк для функций от n переменных равно 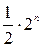 =2n-1 и, следовательно, число функций от n переменных, относящихся к классу S, равно
=2n-1 и, следовательно, число функций от n переменных, относящихся к классу S, равно  . Из элементарных функций самодвойственными являются только тождественная функция х и отрицание
. Из элементарных функций самодвойственными являются только тождественная функция х и отрицание 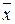 .
.
Лемма о несамодвойственной функции
Если функция алгебры логики не принадлежит классу самодвойственных функций, то всегда можно указать такую замену её переменных функциями х и 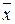 , что в результате этой замены будет получена константа 0 или 1.
, что в результате этой замены будет получена константа 0 или 1.
4) Класс монотонных функций. Обозначение: М.
Функция f(x1,x2,…,xn)ÎP2 называется монотонной, если для любых двух наборов a=(a1,a2,…,an) и b=(b1,b2,…,bn) таких, что ai £ bi, где i=1,2,…,n, следует f(a) £ f(b). Про такие наборы говорят, что набор a предшествует набору b, и обозначают a £ b. Из элементарных функций монотонными являются 0, 1, тождественная функция х, &, Ú. А функции 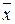 , ®, ½, ¯, Å, º монотонными не являются.
, ®, ½, ¯, Å, º монотонными не являются.
Лемма о немонотонной функции
Если функция алгебры логики не принадлежит классу монотонных функций, то из неё путем подстановки констант 0, 1 и функции х на места переменных можно получить функцию 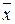 .
.
5) Класс линейных функций. Обозначение: L.
L={f(x1,x2,…,xn)ÎP2: f(x1,x2,…,xn)=c0Åc1×x1Åc2×x2Å…Åcn×xn, где c0,c1,c2,…,cn равны 0 или 1}. Таким образом, этот класс состоит из тех функций алгебры логики, которые представимы линейным выражением. Различные линейные функции от n переменных отличаются друг от друга составом слагаемых, входящих в их линейные выражения. Этот состав определяется значением коэффициентов: если соответствующий коэффициент равен нулю, то слагаемое отсутствует. И так как число коэффициентов равно n+1, то число функций от n переменных, относящихся к классу L, равно 2n+1. Из элементарных функций линейными являются тождественная функция х, отрицание 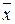 , константы 0 и 1, а также Å и º.
, константы 0 и 1, а также Å и º.
Лемма о нелинейной функции
Если функция алгебры логики от n переменных f(x1,x2,…,xn) нелинейна, то из неё можно получить х1& x2 путем подстановки констант 0 или 1 и функций х и 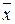 , а также, возможно, размещением знака отрицания над f.
, а также, возможно, размещением знака отрицания над f.
| Т0 | Т1 | S | M | L | |
| + | – | – | + | + | |
| – | + | – | + | + | |
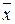 | – | – | + | – | + |
| Таблица 8 |
Отметим, что все замкнутые классы попарно различны. Это хорошо видно из таблицы 8, где знаком «+» отмечена принадлежность функций 0, 1 и 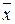 к классу, а знаком «–» отсутствие соответствующей функции в классе.
к классу, а знаком «–» отсутствие соответствующей функции в классе.
Следующая теорема является необходимым и достаточным условием полноты системы функций алгебры логики.
Теорема Поста о полноте
Система функций алгебры логики является полной тогда, и только тогда, когда она целиком не содержится ни в одном из пяти замкнутых классов: Т0, Т1, S, M и L. Иными словами среди функций этой системы обязательно имеются функции, не сохраняющие ноль и единицу, а также несамодвойственная, немонотонная и нелинейная функции.
Следствие 1: из всякой полной в Р2 системы функций можно выделить полную подсистему, содержащую не более четырех функций.
Следствие 2: всякий замкнутый класс функций алгебры логики, не совпадающий с множеством всех функций алгебры логики, содержится по крайней мере в одном из классов Т0, Т1, S, M или L.
В этом смысле классы Т0, Т1, S, M и L являются максимальными или предполными, поскольку добавление к любому из них любой истинностной функции, не принадлежащей классу, приводит к полной системе функций.
Следствие 3: в алгебре логики существует только пять предполных классов: Т0, Т1, S, M и L.
Полная система функций алгебры логики называется базисом в Р2, если никакая её собственная подсистема не является полной. Иными словами базис – это минимальная по числу функций полная система. Важно, что любая из функций алгебры логики записывается формулой через функции базиса.
Используя теорему о полноте, несложно установить, является ли полной заданная система функций и образует ли она базис? Рассмотрим решение этого вопроса на примере.
Пусть имеется система функций: {0, 1, ®, Å, Ø}. Очевидно, что эта система является функционально полной, поскольку полна её собственная подсистема {Ø, ®}. Понятно также, что исходная система функций не является базисом, т.к. из неё можно удалить функции 0, 1 и Å, и оставшиеся функции все ещё составляют полную систему. Выясним теперь, имеются ли в заданной системе другие полные подсистемы, образующие базис. Для этого составим таблицу принадлежности функций {0, 1, ®, Å, Ø} пяти замкнутым классам.
| Т0 | Т1 | S | M | L | |
| + | – | – | + | + | |
| – | + | – | + | + | |
| ® | – | + | – | – | – |
| Å | + | – | – | – | + |
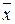 | – | – | + | – | + |
| Таблица 9 |
Из таблицы 9 видно, что базисами являются следующие множества функций: {Ø, ®}, {0, ®}, {Å,® }. Других базисов в данной системе нет.
