При решении задач по физике
Геометрический подход к физическим задачам наследуется еще от древних греков. Смещение от числовых, или скалярных, координат из аналитической геометрии к житейскому понятию направление, смешанному с иллюстративно-художественным подходом, постепенно трансформировало образы мышления физиков.
На уроках физики учитель дает определение радиус-вектора при изучении механических явлений. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку пространства. Многие физические величины характеризуются подобно радиус-вектору не только числовым значением, но и направлением. Например, скорость, перемещение, импульс, напряженность электрического поля, сила. Эти физические величины называют векторными. Длину такого вектора называют модулем вектора. Законы сложения и вычитания векторов также используют на уроках физики неоднократно, изучая разные темы в разных классах. Интуитивное понимание вектора у учащихся складывается с первых же уроков физики в 7 и 8 классе.
Проведем сравнение понятия вектора в физике и математике:
| в физике | в математике |
| Изучаем векторные величины (F, v, S ) | Изучаем векторы (a, b, c ) |
| Вектор имеет точку приложения (на теле) | Вектор можно отложить от любой точки плоскости |
| Правила сложения векторов | |
| Чаще применяем правило параллелограмма | Правило треугольника и правило параллелограмма |
| Длину вектора называем длиной | Длину вектора называем модулем |
Понимание вектора в физике и математике происходит поэтапно, когда ученики раскрывают и изучают следующие вопросы:
В математике:
· Координатная прямая.
· Координатная плоскость.
· Координаты точки.
В физике:
· Понятие системы отсчета.
· Координаты, которыми задается положение тела на прямой, на плоскости, в пространстве, и их количество.
Понятие вектор и нулевой вектор, в каком случае проекция вектора на ось считается положительной, отрицательной, равной нулю, - рассматривается как в математике, так и в физике.
Координаты вектора в физике рассматриваем относительно перемещения тела.
Интеграцию обоих предметов необходимо осуществлять при изучении сложения векторов. В математике это правило треугольника, параллелограмма, многоугольника, произведение векторов. В физике прикладной характер правил сложения векторов виден не при определении перемещения тела, а при сложении скоростей движущегося тела, при вычислении механической работы.
| В математике: | В физике: | |
| Координатная прямая. Координатная плоскость. Координаты точки. | Понятие системы отсчета. Координаты, которыми задается положение тела на прямой, на плоскости, в пространстве, и их количество. | |
| Вектор - направленный отрезок. | Вектор – как графическое представление перемещения тела. При прямолинейном движении в одном направлении путь и перемещение совпадают. 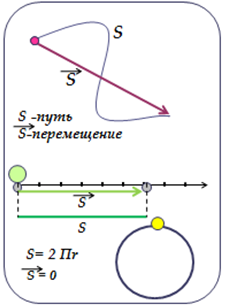 | |
| Точка - это вектор нулевой длины или нулевой вектор. | Если начальное и конечное положение тела совпадают, то вектор перемещения равен нулю. При этом путь может иметь значение отличное от нуля. Например, когда тело движется по окружности.  | |
| В каком случае проекция вектора на ось считается положительной, отрицательной, равной нулю? (Если от проекции начала вектора к проекции его конца надо двигаться по направлению оси, то проекция вектора на ось считают положительной. Если от проекции начала вектора к проекции его конца надо двигаться в направлении, противоположном направлению оси, то проекция отрицательная. Если вектор перпендикулярен оси координат, то проекция равна нулю). | ||
| Чтобы найти координаты вектора, необходимо из координат конца вектора вычесть координаты начала. x=x2-x1 , y=y2-y1 . | Вспомните, как связаны проекция вектора перемещения и координаты тела. (sx= х - х0, sy= y - y0)  Вспомним формулы для расчета координат тела в любой момент времени (х = х0 + sx, y = y0+ sy). Вспомним формулы для расчета координат тела в любой момент времени (х = х0 + sx, y = y0+ sy). 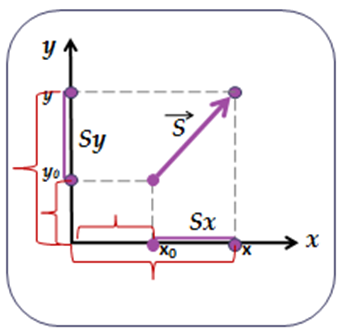 | |
| Операции сложения векторов. | ||
Правило треугольника.  Правило параллелограмма. Правило параллелограмма. 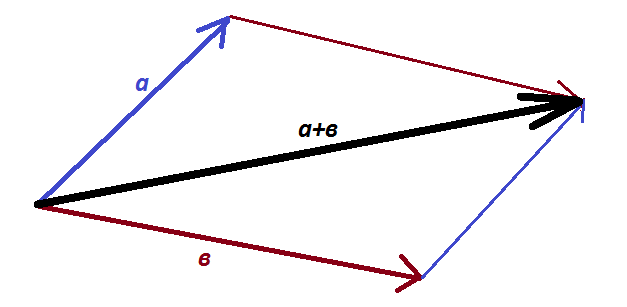 Правило многоугольника. Правило многоугольника. 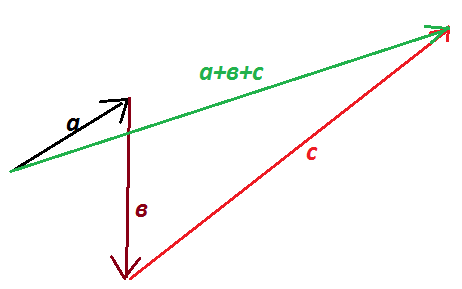 | При движении тела (материальной точки) его перемещение можно рассматривать как геометрическую сумму нескольких последовательных перемещений, например, 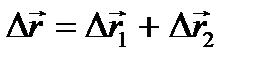 . Соответствующий многоугольник (треугольник) перемещений выглядит таким образом: . Соответствующий многоугольник (треугольник) перемещений выглядит таким образом: 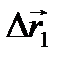  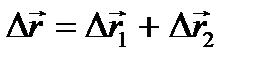 Если тело движется с постоянным по величине и направлению ускорением Если тело движется с постоянным по величине и направлению ускорением 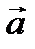 , то выражение для скорости в любой момент t времени имеет вид: , то выражение для скорости в любой момент t времени имеет вид:  . . 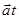 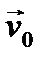  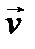 Прикладной характер правил сложения векторов виден не только при определении перемещения тела, но и при сложении скоростей движущегося тела. Прикладной характер правил сложения векторов виден не только при определении перемещения тела, но и при сложении скоростей движущегося тела.  | |
Произведение векторов изучают в 9 классе:  Произведение векторов – скалярная величина. Произведение векторов – скалярная величина. | Вычисление механической работы (в 10 классе):  Механическая работа – скалярная величина. Механическая работа – скалярная величина. | |
Глубокое понимание вектора и действий с векторами у учеников сложится только посредством интеграции математического и физического определения этих понятий.
Рассмотрим пример задачи, при решении которой применяется теорема Пифагора.
 Задача индийского математика XII века Бхаскары.
Задача индийского математика XII века Бхаскары.
На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Решение: По теореме Пифагора  . Высота тополя равна
. Высота тополя равна 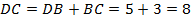 м.
м.
На уроках физики ученики сталкиваются с теоремой Пифагора чаще всего при изучении механических и оптических явлений.
В приложении к данному выступлению можно ознакомиться с подборкой задач на применение векторного анализа и правила треугольника (Приложение 3).
