Свойства определителей

В.Ш. Ройтенберг, Л.А. Сидорова

ЛИНЕЙНая АЛГЕБРа

И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Рекомендовано

научно-методическим советом университета

в качестве учебного пособия

Ярославль 2015

УДК 517(07)

ББК 22.1

Р65

Ройтенберг, В. Ш.

Р65 Линейная алгебра и аналитическая геометрия: Учебное пособие / В.Ш. Ройтенберг, Л.А. Сидорова. – Ярославль: Издат. дом ЯГТУ, 2015. –

ISBN

В каждом разделе приводятся основные понятия, утверждения и формулы, подробно разбираются решения типовых задач, даны задачи для самостоятельного решения. Даны варианты тестов по темам: «матрицы и системы линейных уравнений», «векторная алгебра» и «аналитическая геометрия».

Предназначено для студентов технических и экономических специальностей при изучении курса математики.

УДК 517(07)

ББК 22.1

Рецензенты:.

ISBN

ãЯрославский государственный технический университет, 2015

ОГЛАВЛЕНИЕ

	Предисловие…………………………………………………………...
1.	Определители………………………………………………………….
2.	Операции над матрицами…………………………………………….
3.	Решение систем линейных уравнений………………………………
4.	Ранг матрицы………………………………………………………….
5.	Линейные операции над векторами………………………………….
6.	Линейные операторы…………………………………………………
7.	Декартова система координат………………………………………..
8.	Скалярное произведение……………………………………………..
9.	Векторное и смешанное произведения……………………………...
10.	Плоскость и прямая в пространстве…………………………………
11.	Прямая на плоскости………………………………………………….
12.	Кривые второго порядка……………………………………………..
	Библиографический список
	ПРИЛОЖЕНИЕ. ОБРАЗЦЫ ТЕСТОВ
	Ответы

ПРЕДИСЛОВИЕ

Настоящее пособие предназначено студентам, изучающим курс линейной алгебры и аналитической геометрии в объеме программы для высших технических заведений.

Линейная алгебра и аналитическая геометрия – первый математический курс, который студенты изучают в вузе. Матрицы, определители, системы линейных уравнений, линейные операторы, уравнения плоскостей и прямых – вопросы, значительно отличающиеся от того, с чем студенты имели дело в школе. Чтобы этот большой и новый для студента материал был усвоен за небольшое время, отведенное на его изучение, необходима систематическая работа по освоению терминологии, основных понятий и методов. Предлагаемое пособие предназначено для помощи студентам в организации такой работы.

Пособие можно использовать в самостоятельной работе студентов при выполнении расчетно-графической работы, при подготовке к практическим занятиям, к контрольным работам (тестам), к зачету или экзамену, а также как задачник на практических занятиях.

Пособие содержит 12 разделов и приложение. Каждый раздел делится на три части.

В первой части излагаются основные понятия, утверждения и формулы, изучаемые в разделе.

Во второй части даются примеры решения типовых задач. Они предназначены как для иллюстрации изучаемых понятий и формул, так и для демонстрации техники вычислений и методов решения задач. Решения даются с систематическими ссылками на соответствующие теоретические положения и формулы из первой части, они содержат подробные выкладки, геометрические задачи сопровождаются рисунками.

В третьей части даны задачи для самостоятельного решения. Часть задач аналогична решенным в качестве примера, к некоторым даны указания по методу решения, нужным формулам и т.п. Ответы к задачам даны в конце пособия.

В приложении приводятся по два варианта заданий каждой из трех контрольных работ в виде тестов, которые даются студентам ЯГТУ. Темы контрольных: 1) матрицы и системы линейных уравнений, 2) векторная алгебра, 3) аналитическая геометрия. Для одного варианта даны решения, для другого только ответы.

ОПРЕДЕЛИТЕЛИ

Основные понятия и формулы

Матрицы

Матрицей размера (или просто -матрицей) называется прямоугольная таблица чисел (элементов матрицы) из строк и столбцов. При конкретных значениях и задать матрицу можно, просто записав эту таблицу; например,

, , –

разные формы записи одной и той же -матрицы. Мы будем пользоваться записью в круглых скобках. В общем случае матрица обычно обозначается прописной буквой, например, , а ее элемент, стоящий в -ой строке, -м столбце, соответствующей строчной буквой с индексами и . Обозначения:

, , .

Для матрицы , например, , а .

Задать -матрицу означает задать правило вычисления любого ее элемента по номерам строки и столбца , в которых он находится.

Матрица размера называется квадратной матрицей -го порядка:

.

Числа , ,…, образуют главную диагональ квадратной матрицы.

Квадратная матрица называется (верхне)треугольной, есливсе ее элементы, расположенные ниже главной диагонали, равны нулю: при . Важная роль треугольных матриц будет ясна из дальнейшего.

-матрицу часто называют строкой или арифметическим вектором-строкой длины , -матрицу – столбцом или арифметическим вектором-столбцом высоты .

Понятие определителя

Для каждой квадратной матрицы 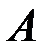-го порядка ( ) определено число, обозначаемое или и называемое определителем матрицы 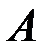(определителем -го порядка).

При матрица состоит из одного элемента,

.

При

. (1.1)

При любом – сумма всевозможных произведений элементов матрицы , стоящих в разных строках и разных столбцах, со знаком или , определяемым порядком сомножителей:

. (1.2)

Здесь:

сомножители ,, …, выбраны последовательно из 1-ой, 2-ой, …, -ой строки;

– соответствующая последовательность номеров столбцов;

– число инверсий в последовательности : число и число с большим номером ( ) образуют инверсию, если . При четных величина , при нечетных – .

Формула (1.1), конечно, частный случай общей формулы (1.2) (см. пример 1.2.6).

При формула (1.2) принимает вид

. (1.3)

Из (1.2) следует, что определитель треугольной матрицы равен произведению элементов главной диагонали: .

Свойства определителей

Здесь для краткости под элементами, строками и столбцами определителя мы будем понимать элементы, строки и столбцы соответствующей матрицы.