Иррациональные уравнения
Иррациональные уравнения и неравенства довольно часто встречаются в материалах вступительных экзаменов различных высших учебных заведений. Разделы Единого государственного экзамена по математике также включают данную тематику как в простых случаях (части А и В), так и в более сложных (часть С). Некоторые правила и особенности решения таких уравнений и неравенств изложены в настоящем разделе.
Уравнение, содержащее неизвестное под знаком радикала, называется иррациональным. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней, поэтому следует проверять корни подстановкой в исходное уравнение.
При решении уравнений необходимо учитывать следующее:
1) если показатель радикала – четное число, то подкоренное выражение должно быть неотрицательно, при этом значение радикала также является неотрицательным;
2) если показатель радикала – нечетное число, то подкоренное выражение может быть любым действительным числом, в этом случае знак радикала совпадает со знаком подкоренного выражения.
Пример 1. Решить уравнение:
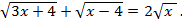
Решение. Найдем область допустимых значений переменной. Поскольку корни четной степени, то подкоренные выражения должны быть неотрицательны:
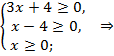
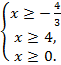
Решение данной системы неравенств есть область допустимых значений переменной (или область определения уравнения).
Возведем обе части уравнения в квадрат:
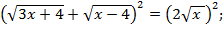
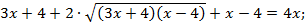
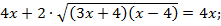
2 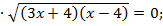
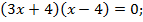 или
или 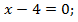
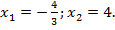
Значение 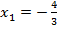 не входит в область допустимых значений, поэтому является посторонним корнем для исходного уравнения.
не входит в область допустимых значений, поэтому является посторонним корнем для исходного уравнения.
Проверим, удовлетворяет ли х = 4 уравнению, для этого подставим х = 4 в уравнение:
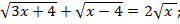
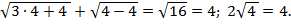
4 = 4, поэтому х = 4 – корень исходного уравнения.
Ответ: х = 4.
Пример 2. Решить уравнение:
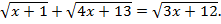
Решение. Допустимые значения переменной должны удовлетворять системе неравенств:
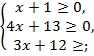
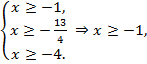
Областью допустимых значений являются 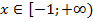 . Возведем левую и правую части уравнения в квадрат:
. Возведем левую и правую части уравнения в квадрат:
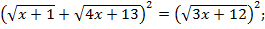
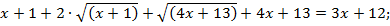
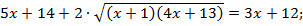
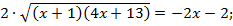
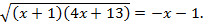
Вновь возведем левую и правую части уравнения в квадрат:
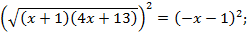
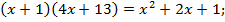
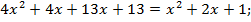
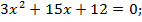
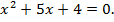
Корни могут быть найдены по теореме Виета:
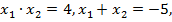 откуда
откуда 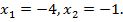
Корень 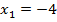 не входит в область допустимых значений, т. е. является посторонним корнем для исходного уравнения. Проверим корень
не входит в область допустимых значений, т. е. является посторонним корнем для исходного уравнения. Проверим корень 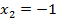 , подставив его в уравнение:
, подставив его в уравнение:
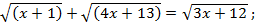
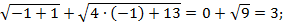
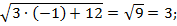
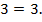
Ответ: 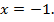
Замечание:
Получив выражение 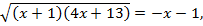 можно было заметить, что должно выполняться неравенство
можно было заметить, что должно выполняться неравенство 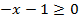 или
или 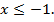 Совмещая эти значения с областью допустимых значений, где
Совмещая эти значения с областью допустимых значений, где 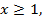 получаем единственно возможный корень
получаем единственно возможный корень 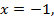 который и надо было проверить.
который и надо было проверить.
Пример 3. Решить уравнение:
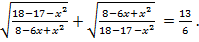
Решение. При решении этого уравнения можно сразу ввести замену переменной, обозначив один корень за у, а другой за  . Можно идти и традиционным путем, начиная с области допустимых значений.
. Можно идти и традиционным путем, начиная с области допустимых значений.
Областью допустимых значений является решение системы неравенств:
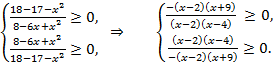
Поскольку 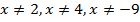 то уравнение может быть записано в виде:
то уравнение может быть записано в виде:
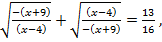 тогда область допустимых значений удовлетворяет системе,
тогда область допустимых значений удовлетворяет системе,
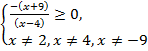
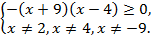
Решим неравенство методом интервалов (рис. 7.1).
|

Рис. 7.1.Метод интервала.
Область допустимых значений 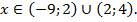
Обозначим 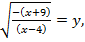 где
где 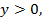 тогда
тогда 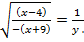
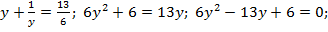
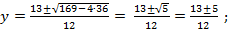
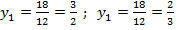
Пусть 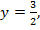 тогда
тогда 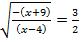
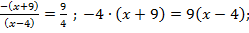
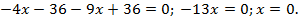
Пусть 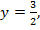 тогда
тогда 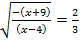
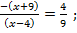
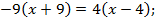
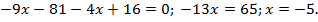
Оба корня х = 0 и х = – 5 принадлежат области допустимых значений. Выполним проверку.
Если х = 0, тогда
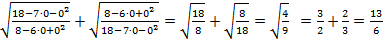
Если х = – 5, тогда
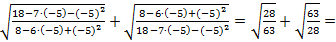
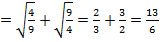
Ответ: х = 0, х = – 5.
Пример 4. Решить уравнение:
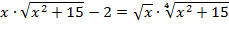
Решение. Допустимыми значениями переменной являются 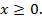 Обозначим
Обозначим 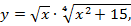 где
где 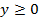 .
.
Уравнение примет вид 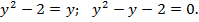
По теореме Виета 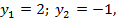 где
где 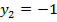 посторонний корень, не удовлетворяющий ограничению
посторонний корень, не удовлетворяющий ограничению 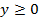 .
.
Если у = 2, тогда 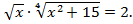
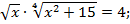
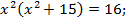
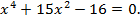
Полученное биквадратное уравнение сведем к квадратному уравнению заменой 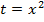 , где
, где 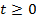 ,
,
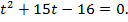
По теореме Виета 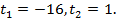 Поскольку
Поскольку 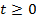 , то
, то 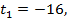 – посторонний корень. Если
– посторонний корень. Если 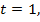 то
то 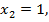 откуда
откуда 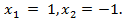 Но
Но 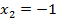 не входит в область допустимых значений, поэтому
не входит в область допустимых значений, поэтому 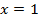 .
.
Сделаем проверку:
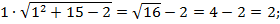
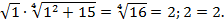
Ответ: х = 1.
Пример 5. Решить уравнение:
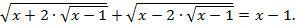
Решение. Допустимые значения неизвестного удовлетворяют условиям,
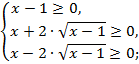
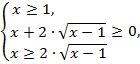
Второе неравенство справедливо для 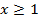 , при этих же значениях переменной левая и правая часть третьего неравенства неотрицательны, поэтому его можно решить возведением в квадрат:
, при этих же значениях переменной левая и правая часть третьего неравенства неотрицательны, поэтому его можно решить возведением в квадрат:
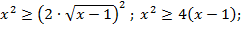
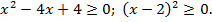
Неравенство выполняется для любых действительных значений переменной. Таким образом, областью допустимых значений переменной являются 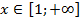 . Возведем в квадрат левую и правую часть уравнения:
. Возведем в квадрат левую и правую часть уравнения:
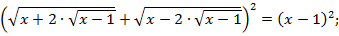
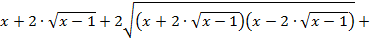
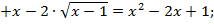
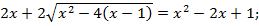
2 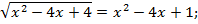
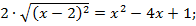
2 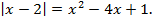
Если 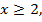 то
то 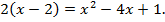
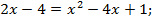
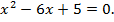
По теореме Виета х1 = 5, х2= 1.
Условию 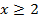 удовлетворяет только значение
удовлетворяет только значение 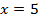 .
.
Если 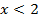 , то
, то 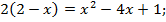
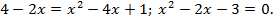
По теореме Виета 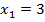 ,
, 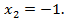 Первое из значений
Первое из значений 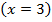 не удовлетворяет условию
не удовлетворяет условию 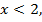 второе значение
второе значение 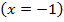 не принадлежит области допустимых значений, поэтому оба значения
не принадлежит области допустимых значений, поэтому оба значения 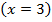 и
и 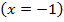 не являются корнями уравнения. Выполним проверку для
не являются корнями уравнения. Выполним проверку для 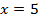 :
:
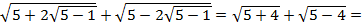
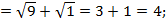
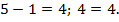
Ответ: 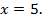
Замечание. Возможен другой вариант решения: в исходном уравнении подкоренные выражения являются полными квадратами; обозначив 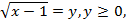 получим
получим
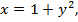 и уравнение примет вид :
и уравнение примет вид :
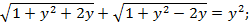
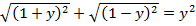
или 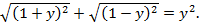
Если 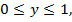 то
то 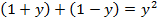
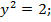
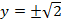 – оба значения не удовлетворяют условию
– оба значения не удовлетворяют условию
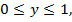
Если 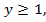 то
то 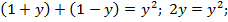
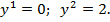
Условию 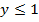 удовлетворяет значение
удовлетворяет значение 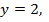
откуда 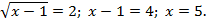
Остается лишь выполнить проверку.
В некоторых случаях решение может быть получено дополнением уравнения до формул сокращенного умножения (разности квадратов и кубов, суммы кубов). При этом используется известное правило, что уравнение не изменится, если левую и правую его часть умножить на одно и то же отличное от нуля выражение.
Пример 6. Решить уравнение:
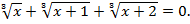
Решение. Областью допустимых значений являются все действительные значения переменной. Запишем уравнение в виде 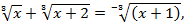 и домножим левую и правую часть на неполный квадрат разности так, чтобы в левой части получить формулу суммы кубов:
и домножим левую и правую часть на неполный квадрат разности так, чтобы в левой части получить формулу суммы кубов:
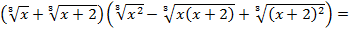
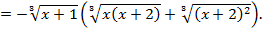
Заметим, что 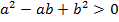 для любых действительных значений a и b, следовательно, обе части уравнения умножены на одно и то же положительное выражение:
для любых действительных значений a и b, следовательно, обе части уравнения умножены на одно и то же положительное выражение:
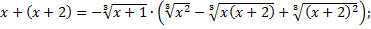
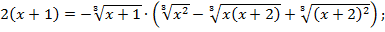
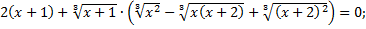
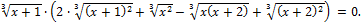
Произведение сомножителей равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю. Второй из сомножителей не может обращаться в ноль, так как
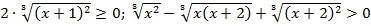
для любых действительных значений х, поэтому:
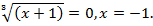
Сделаем проверку:
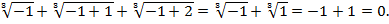
Ответ: