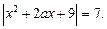Дробно-рациональные уравнения
Стандартный вид дробно-рационального уравнения:
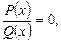 (3.8)
(3.8)
где 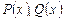 – многочлены.
– многочлены.
Область допустимых значений (ОДЗ) данного уравнения: 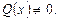 Решение уравнений (3.8) сводится к решению системы
Решение уравнений (3.8) сводится к решению системы
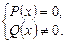
Дробно-рациональные уравнения вида
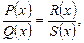
где 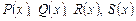 – многочлены, можно решать, используя основное свойство пропорции:
– многочлены, можно решать, используя основное свойство пропорции:
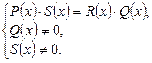
К основному методу решения дробно-рациональных уравнений относится также метод замены переменной.
Некоторые специальные приемы будут рассмотрены далее на примерах.
Пример 1. Решить уравнение 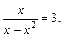
Решение. Сводим заданное уравнение к стандартному виду (3.8):
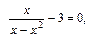 т. е.
т. е. 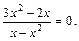
Его решением будет решение системы
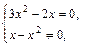 т. е.
т. е. 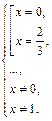
Значит, решением заданного уравнения является 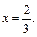
Пример 2. Решить уравнение 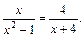
Решение. Применим основное свойство пропорции с учетом ОДЗ уравнения:
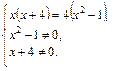
Получаем:
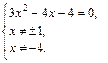
Откуда
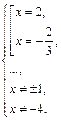
Оба корня являются решениями, так как подходят по ОДЗ. В ответе имеем:
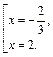
Пример 3.Решить уравнение 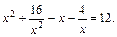
Решение. Группируем слагаемые
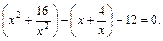
Заменяем
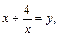 откуда
откуда
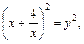 т. е.
т. е. 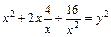 и
и 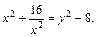
Получаем уравнение 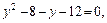 или, то же самое,
или, то же самое, 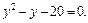
Полученное уравнение имеет корни: 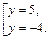
Возвращаемся к переменной х:
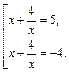
В результате приходим к совокупности 2-х квадратных уравнений
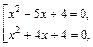
которые решаем на ОДЗ: 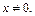 Приходим к ответу
Приходим к ответу
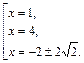
Пример 4.Решить уравнение 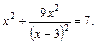
Решение. Выделим в левой части уравнения полный квадрат суммы:
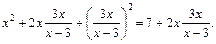
Получаем уравнение, которое приобретает вид
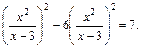
Заменяем 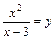 и приходим к уравнению
и приходим к уравнению
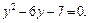
Решая его, найдем корни:
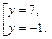
Возвращаемся к старой переменной:
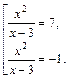
Решаем полученные уравнения по свойству пропорции (с учетом ОДЗ):
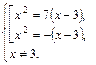
Приходим к ответу 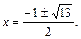
Пример 5.Решить уравнение 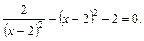
Решение. Введем замену: 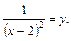
Тогда 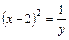 и получим уравнение
и получим уравнение 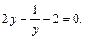
Решаем его:
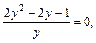 т. е.
т. е. 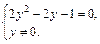
Решая квадратное уравнение, находим корни:
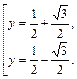
Вернемся к переменной х:
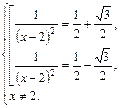
Решаем первое уравнение:
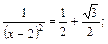
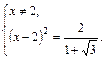
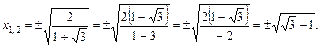
Второе уравнение не имеет решения, так как 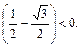
Получили ответ: 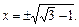
Задания
I уровень
1.1. Решите уравнение:
1) 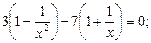 2)
2) 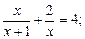
3) 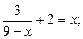 4)
4) 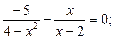
5) 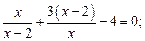 6)
6) 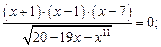
7) 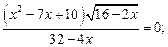 8)
8) 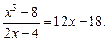
II уровень
2.1. Решите уравнение:
1) 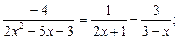 2)
2) 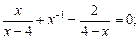
3) 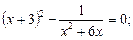 4)
4) 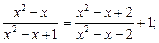
5) 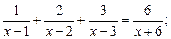 6)
6) 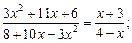
7) 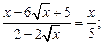 8)
8) 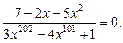
III уровень
3.1. Решите уравнение:
1) 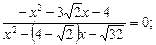 2)
2) 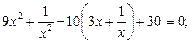
3) 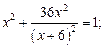 4)
4) 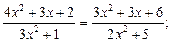
5) 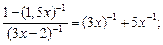 6)
6) 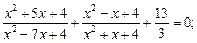
7) 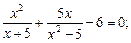 8)
8) 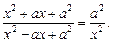
3.2. Найдите квадрат суммы корней 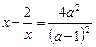 при
при 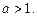
3.3. Определите при каких значениях а уравнение имеет действительные корни:
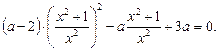
Уравнения с модулем
Модулем (абсолютной величиной) числа 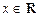 называется неотрицательное число:
называется неотрицательное число:
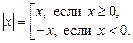 (3.9)
(3.9)
Геометрическая интерпретация модуля: 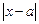 – это расстояние от точки а до точки х на координатной оси, в частности,
– это расстояние от точки а до точки х на координатной оси, в частности, 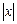 – это расстояние от точки 0 до точки х.
– это расстояние от точки 0 до точки х.
Свойства модуля:
1) 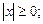 2)
2) 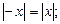 3)
3) 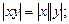
4) 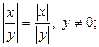 5)
5) 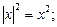 6)
6) 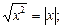
7) 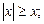 8)
8) 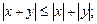 9)
9) 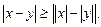
Пусть 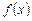 – некоторое алгебраическое выражение. Тогда, используя определение модуля (3.9) при соответствующих предположениях, можно раскрыть знак абсолютной величины данного выражения:
– некоторое алгебраическое выражение. Тогда, используя определение модуля (3.9) при соответствующих предположениях, можно раскрыть знак абсолютной величины данного выражения:
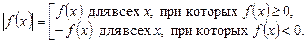
Уравнение, содержащее выражение с неизвестной х под знаком модуля, называется уравнением с модулем. Рассмотрим основные типы уравнений с модулем и методы их решения.
I тип: уравнение вида
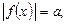 (3.10)
(3.10)
где а – число, 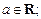
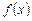 – некоторое выражение с неизвестной х.
– некоторое выражение с неизвестной х.
1. Если 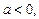 уравнение (3.10) решений не имеет.
уравнение (3.10) решений не имеет.
2. Если 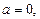 уравнение (3.10) равносильно уравнению
уравнение (3.10) равносильно уравнению 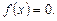
3. Если 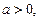 уравнение (3.10) равносильно совокупности уравнений:
уравнение (3.10) равносильно совокупности уравнений: 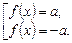
II тип: уравнение вида
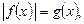
где 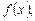
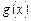 – некоторые выражения с неизвестной х.
– некоторые выражения с неизвестной х.
Решать это уравнение можно несколькими способами.
1-й способ – используя определения модуля:
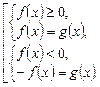
2-й способ – используя подход к решению, как к уравнениям I типа с дополнительным условием на знак выражения 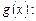
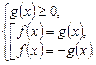
З а м е ч а н и е. 1-й или 2-й способ решения таких уравнений выбирают в зависимости от того, какое из неравенств 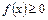 или
или 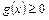 решается легче.
решается легче.
3-й способ – метод интервалов. Необходимо:
1) найти те значения х, для которых 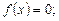
2) нанести полученные значения х на числовую ось;
3) определить знаки 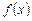 для каждого из полученных интервалов;
для каждого из полученных интервалов;
4) нарисовать кривую знаков;
5) решить уравнение на каждом промежутке в отдельности, раскрывая модуль согласно рисунку;
6) для каждого конкретного промежутка проверить, принадлежат ли полученные корни этому промежутку;
7) в ответе указать совокупность всех полученных корней.
III тип:уравнения, содержащие несколько модулей. Если их два, то это уравнение вида
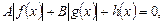 (3.11)
(3.11)
где 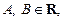
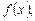
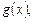
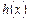 – некоторые выражения с неизвестной х.
– некоторые выражения с неизвестной х.
1-й способ – можно использовать определение модуля и рассматривать 4 случая возможных знаков 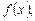
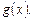 Этот способ, как правило, не является рациональным.
Этот способ, как правило, не является рациональным.
2-й способ –метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей в уравнении. Для уравнения (3.11) рисуют две оси, располагая их одна под другой (одна ось для 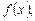 вторая – для
вторая – для 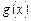 ). Для каждого выражения
). Для каждого выражения 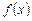 и
и 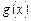 следует изобразить кривую знаков на соответствующей оси. Затем раскрывают модули, используя рисунок, и решают уравнение отдельно на каждом промежутке. Подходят только те корни, которые принадлежат рассматриваемому промежутку. В ответе необходимо указать совокупность полученных корней.
следует изобразить кривую знаков на соответствующей оси. Затем раскрывают модули, используя рисунок, и решают уравнение отдельно на каждом промежутке. Подходят только те корни, которые принадлежат рассматриваемому промежутку. В ответе необходимо указать совокупность полученных корней.
IV тип: уравнение вида
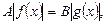 (3.12)
(3.12)
где 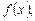
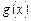 – некоторые выражения с неизвестной х;
– некоторые выражения с неизвестной х; 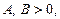
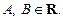
1-й способ – решение уравнения (3.12) сводится к решению совокупности уравнений:
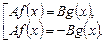
2-й способ – метод интервалов (не рационально).
3-й способ – после возведения уравнения в квадрат и использования свойства модуля 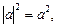 уравнение сводится к равносильному:
уравнение сводится к равносильному:
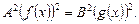
Полученное уравнение решается в зависимости от его типа.
V тип: уравнения, решаемые заменой переменной, например:
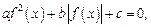
где 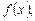
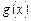 – некоторые выражения с неизвестной х;
– некоторые выражения с неизвестной х; 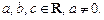
По свойству модуля оно записывается в виде
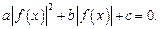
Вводят замену 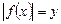 и решают полученное квадратное уравнение относительно неизвестной у. Затем необходимо вернуться к старой переменной. В случае 2-х различных корней
и решают полученное квадратное уравнение относительно неизвестной у. Затем необходимо вернуться к старой переменной. В случае 2-х различных корней 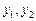 квадратного уравнения это будет совокупность уравнений I типа:
квадратного уравнения это будет совокупность уравнений I типа:
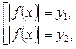
если корень 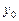 единственный, то остается решить уравнение
единственный, то остается решить уравнение 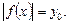
Необходимо помнить, что в случае отрицательного значения 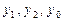 уравнение с модулем не имеет решений.
уравнение с модулем не имеет решений.
Пример 1.Решить уравнение 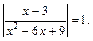
Решение. Это уравнение I типа. Его ОДЗ: 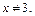
Уравнение записывается в виде 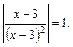
На ОДЗ можно сократить и получаем
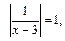 откуда
откуда 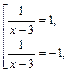 т. е.
т. е. 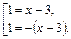
Получаем корни 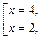 которые подходят по ОДЗ.
которые подходят по ОДЗ.
Пример 2.Решить уравнение 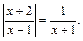
Решение. Это уравнение II типа. Его ОДЗ: 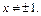 Оно имеет решение, если
Оно имеет решение, если 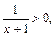 т. е. при
т. е. при 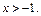 Таким образом, для
Таким образом, для 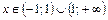 получаем:
получаем:
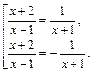 (3.13)
(3.13)
Решим отдельно полученные дробно-рациональные уравнения. Первое уравнение сводится к виду
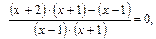 откуда
откуда 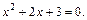
Это квадратное уравнение решений не имеет, так как 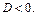
Из второго уравнения совокупности (3.13) получаем
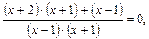 т. е.
т. е. 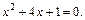
Квадратное уравнение имеет корни:
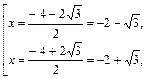
т. е. первый корень не принадлежит множеству 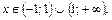 на котором решали уравнение, следовательно, ответом является только
на котором решали уравнение, следовательно, ответом является только 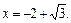
Пример 3. Решить уравнение 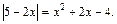
Решение. Имеем уравнение II типа, которое решим по определению модуля:
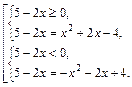 (3.14)
(3.14)
Решаем первую систему совокупности (3.14):
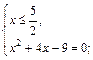
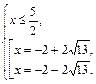
Значение 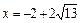 не подходит по условию
не подходит по условию 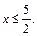 Следовательно, корнем является
Следовательно, корнем является 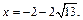
Решаем вторую систему совокупности (3.14):
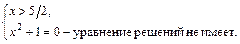
Получили ответ 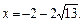
Пример 4.Решить уравнение 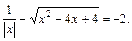
Решение. Поскольку 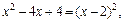 то уравнение записывается в виде
то уравнение записывается в виде
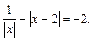
Это уравнение относится к III типу уравнений.
Его ОДЗ: 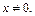 Решим методом интервалов.
Решим методом интервалов.
Нулями выражений, стоящих под модулем, являются 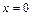 и
и  Эти значения разбивают числовую ось на три промежутка (рис. 3.1).
Эти значения разбивают числовую ось на три промежутка (рис. 3.1).
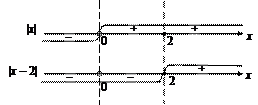 |
Рис. 3.1
Раскрыв модули на каждом из полученных промежутков, с учетом их знаков, получим совокупность систем:
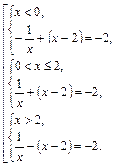
Решим отдельно системы:
I. 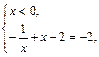 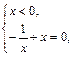 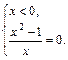 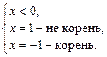 | II. 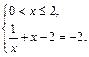 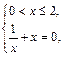 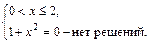 |
III. 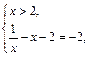
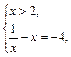
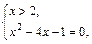
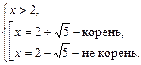
Решением данного уравнения являются значения 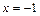 и
и 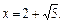
Пример 5. Решить уравнение 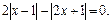
Решение. Запишем уравнение в виде
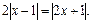
Оно относится к IV типу. Возведем обе его части в квадрат:
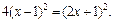 После упрощения имеем:
После упрощения имеем:
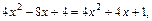 т. е.
т. е. 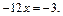
Получаем 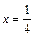 – корень.
– корень.
Пример 6.Решить уравнение 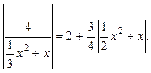
Решение. ОДЗ: 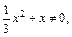 т. е.
т. е. 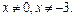
Преобразуем данное уравнение к виду
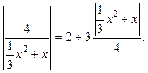
Заменяем 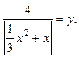
Уравнение приобретает вид
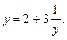
Решаем его как дробно-рациональное и получаем:
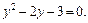
Последнее квадратное уравнение имеет корни:
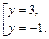
Возвращаясь к переменной х, получаем:
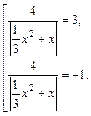
Второе уравнение совокупности решений не имеет, так как слева положительное выражение, а справа – отрицательное.
Первое уравнение совокупности сводится к I типу уравнений с модулем и равносильно совокупности при условии 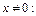
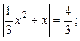
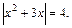
Приходим к совокупности
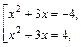 т. е.
т. е. 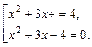
Решение имеет только второе уравнение совокупности, его корни:
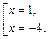
Оба они подходят по ОДЗ.
Пришли к ответу: 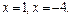
Пример 7.Решить уравнение 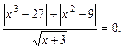
Решение. ОДЗ: 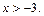
С учетом ОДЗ данное уравнение равносильно уравнению:
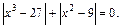
Используя свойства модуля (имеем сумму двух неотрицательных величин), получаем:
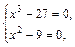
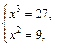
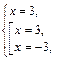
т. е. 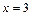 – решение полученной системы, оно подходит по ОДЗ.
– решение полученной системы, оно подходит по ОДЗ.
Получили ответ: 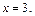
Задания
I уровень
1.1. Решите уравнение:
1) 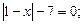 2)
2) 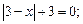
3) 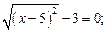 4)
4) 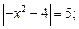
5) 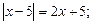 6)
6) 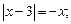
7) 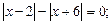 8)
8) 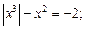
9) 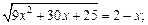 10)
10) 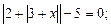
11) 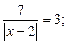 12)
12) 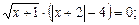
13) 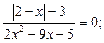 14)
14) 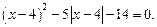
II уровень
2.1. Решите уравнение:
1) 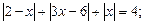 2)
2) 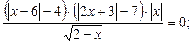
3) 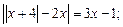 4)
4) 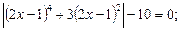
5) 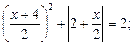 6)
6) 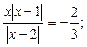
7) 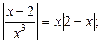 8)
8) 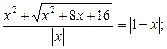
9) 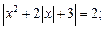 10)
10) 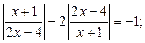
11) 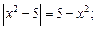 12)
12) 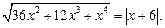
III уровень
3.1. Решите уравнение:
1) 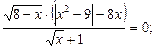 2)
2) 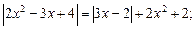
3) 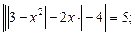 4)
4) 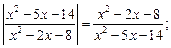
5) 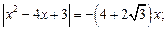 6)
6) 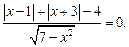
3.2. Найти количество натуральных корней уравнения
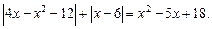
3.3. Решите уравнение:
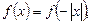 если
если 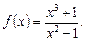
3.4. Найдите все значения а, при которых уравнение 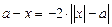 имеет единственный корень.
имеет единственный корень.
3.5.Для каждого значения а найдите множество решений:
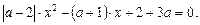
3.6. Определите, при каком значении а уравнение имеет ровно три решения:
1) 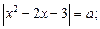 2)
2)