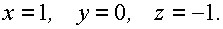Решение систем линейных уравнений матричным методом

Определители

Определитель второго порядка, соответствующий таблице элементов 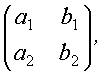определяется разностью 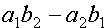и обозначается:

.

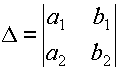Определитель третьего порядка, соответствующий таблице элементов

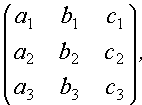определяется равенством: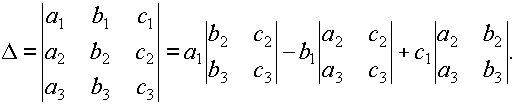

Минором любого элемента определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащие этот элемент.

Алгебраическим дополнением данного элемента называется его минор, умноженный на 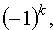где 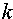– сумма номеров строки и столбца этого элемента.

Определитель третьего порядка можно вычислить диагональным способом. Для этого к определителю последовательно приписываются справа первый и второй столбцы. Произведения элементов, стоящих на главной диагонали, а также на двух параллелях к ней, берутся со знаком плюс; произведения элементов побочной диагонали и на двух параллелях к ней берутся со знаком минус. Алгебраическая сумма этих шести произведений дает определитель третьего порядка

.

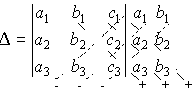Примеры. Вычислить определители:

а)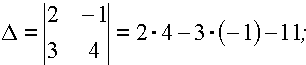

б)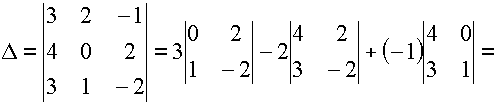

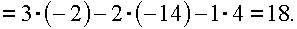
в)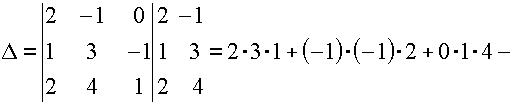

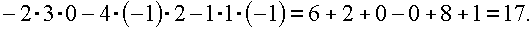
Решение систем линейных уравнений по формулам Крамера

Решение данной системы находится по формулам:

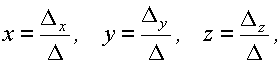
где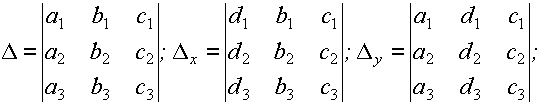

.

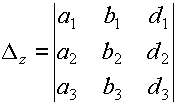При этом предполагается, что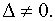

Пример. Решить систему линейных уравнений по формулам Крамера

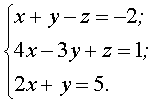
Решение: Вычислим определитель системы

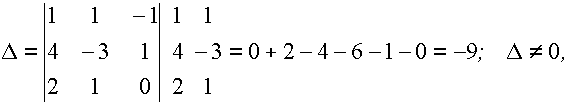
следовательно данная система имеет единственное решение.

Вычислим дополнительные определители:

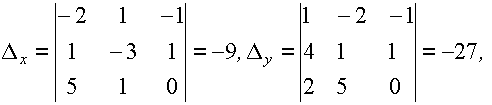
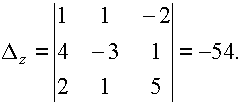
По формулам Крамера находим:

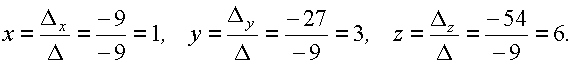
Следовательно, 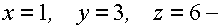решение данной системы.

Матрицы

Прямоугольная таблица чисел, расположенных в m строках и n столбцах называется матрицей размера m x n. Обозначается буквами А, В, С.

,

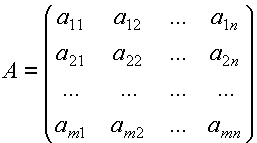где 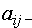элемент матрицы, i – номер строки, j – номер столбца.

Виды матриц

1. Если в матрице число строк равно числу столбцов ( m = n), то она называется квадратной.

2. 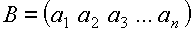- матрица – строка.

3. 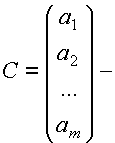матрица-столбец. 4. 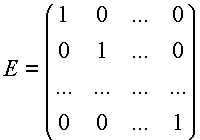единичная матрица.

Операции над матрицами

1. Сложение матриц.

Сумма двух матриц А и В одинаковых размеров называется матрица

С = А + В, элементы которой определяются равенством .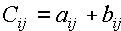

2. Умножение матрицы на число.

При умножении матрицы А на число 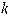, все элементы данной матрицы умножатся на это число.

3. Умножение матриц.

Условия умножения матриц: число столбцов матрицы А должно быть равно числу строк матрицы В.

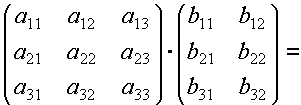
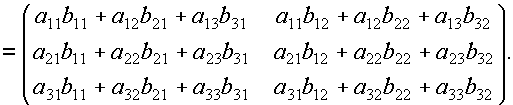
Матрица В называется обратной по отношению к квадратной матрице А, если АВ = ВА = Е. Для матрицы, обратной по отношению к матрицеА, принято обозначение А^-1. Всякая квадратная матрица, если она невырождена (  0), имеет обратную матрицу.

Обратная матрица находится по формуле:

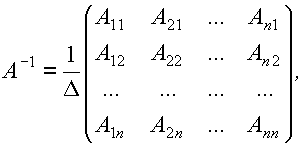
где 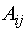– алгебраические дополнения элементов определителя.

Решение систем линейных уравнений матричным методом

Пример. Решить систему матричным методом

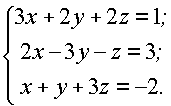
Решение: Перепишем систему в виде АХ = В, где

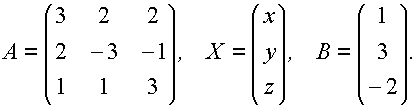
Решение матричного уравнения имеет вид Х = А^-1В.

Найдем обратную матрицу А^-1, для чего вычислим определитель системы:

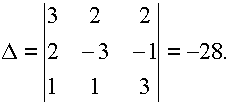
Вычислим алгебраические дополнения элементов определителя:

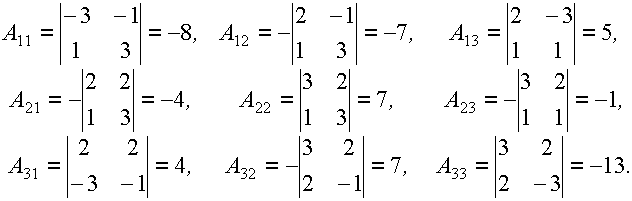
Следовательно,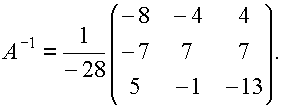

Тогда матрица Х:

.

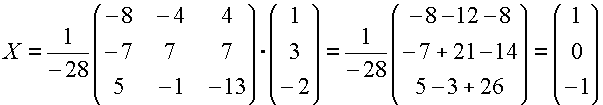Ответ: