Элементы векторной алгебры и аналитической геометрии. Комплексные числа
Задание 1. Даны координаты вершин пирамиды 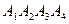 . Требуется найти: 1) длину ребра
. Требуется найти: 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами  и
и  ; 3) угол между ребром
; 3) угол между ребром 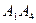 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды; 6) уравнения прямой
; 5) объем пирамиды; 6) уравнения прямой  ; 7) уравнение плоскости
; 7) уравнение плоскости  ; 8) уравнения высоты, опущенной из вершины
; 8) уравнения высоты, опущенной из вершины 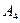 на грань
на грань  . Сделать чертеж.
. Сделать чертеж.
1. 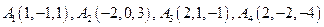
2. 
3. 
4. 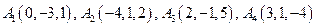
5. 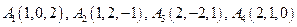
6. 
7. 
8. 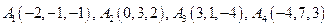
9. 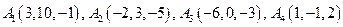
10. 
Задание 2.
1. Написать уравнения сторон треугольника АВС, если задана его вершина  и уравнения двух медиан
и уравнения двух медиан  и
и 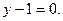 Сделать чертеж.
Сделать чертеж.
2. Написать уравнения сторон треугольника, зная одну его вершину 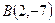 , а также уравнения высоты
, а также уравнения высоты  и медианы
и медианы  , проведенных из различных вершин. Сделать чертеж.
, проведенных из различных вершин. Сделать чертеж.
3. Найти внутренние углы треугольника, если даны уравнения его сторон  и
и  , и основание
, и основание  высоты AD. Сделать чертеж.
высоты AD. Сделать чертеж.
4. Две стороны параллелограмма заданы уравнениями  и
и  . Диагонали его пересекаются в начале координат. Написать уравнения двух других сторон параллелограмма и его диагоналей. Сделать чертеж.
. Диагонали его пересекаются в начале координат. Написать уравнения двух других сторон параллелограмма и его диагоналей. Сделать чертеж.
5. Найти вершины прямоугольного равнобедренного треугольника, если дана вершина прямого угла  и уравнение гипотенузы
и уравнение гипотенузы  Сделать чертеж.
Сделать чертеж.
6. Даны две вершины треугольника 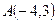 и
и  и точка пересечения высот
и точка пересечения высот  . Найти третью вершину С. Сделать чертеж.
. Найти третью вершину С. Сделать чертеж.
7. Стороны АВ и ВС параллелограмма заданы уравнениями  и
и  , диагонали его пересекаются в точке
, диагонали его пересекаются в точке  . Найти длины его высот. Сделать чертеж.
. Найти длины его высот. Сделать чертеж.
8. Вычислить координаты вершин ромба, если известны уравнения двух его сторон:  и
и  , и уравнение одной из его диагоналей:
, и уравнение одной из его диагоналей: 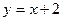 . Сделать чертеж.
. Сделать чертеж.
9. Составить уравнения сторон треугольника, зная одну его вершину  , и уравнения высот
, и уравнения высот 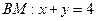 и
и  , где М-точка пересечения высот. Сделать чертеж.
, где М-точка пересечения высот. Сделать чертеж.
10. В треугольнике АВС даны уравнение стороны 
 , уравнение высоты
, уравнение высоты  , уравнение высоты
, уравнение высоты  , где М-точка пересечения высот. Написать уравнения сторон АС, ВС и высоты СМ. Сделать чертеж.
, где М-точка пересечения высот. Написать уравнения сторон АС, ВС и высоты СМ. Сделать чертеж.
Задание 3.
1. Написать уравнение кривой, каждая точка которой находится на одинаковом расстоянии от точки  и от оси
и от оси 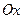 . Сделать чертеж.
. Сделать чертеж.
2. Написать уравнение кривой, сумма квадратов расстояний от каждой точки которой до точек  и
и 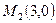 равна 50. Сделать чертеж.
равна 50. Сделать чертеж.
3. Написать уравнение кривой, расстояние от каждой точки которой до точки  вдвое меньше расстояния до точки
вдвое меньше расстояния до точки  . Сделать чертеж.
. Сделать чертеж.
4. Написать уравнение кривой, модуль разности расстояний от каждой точки которой до точек  и
и  равен 4. Сделать чертеж.
равен 4. Сделать чертеж.
5. Написать уравнение кривой, каждая точка которой находится на одинаковом расстоянии от точки 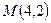 и от оси
и от оси 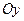 . Сделать чертеж.
. Сделать чертеж.
6. Написать уравнение кривой, каждая точка которой отстоит от точки 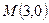 вдвое дальше, чем от прямой
вдвое дальше, чем от прямой  . Сделать чертеж.
. Сделать чертеж.
7. Написать уравнение кривой, для каждой точки которой расстояние от точки  вдвое меньше расстояния от прямой
вдвое меньше расстояния от прямой  . Сделать чертеж.
. Сделать чертеж.
8. Написать уравнение кривой, сумма расстояний от каждой точки которой до точек 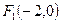 и
и  равна 2
равна 2  . Сделать чертеж.
. Сделать чертеж.
9. Написать уравнение кривой, сумма квадратов расстояний от каждой точки которой до точек  и
и  равна 27. Сделать чертеж.
равна 27. Сделать чертеж.
10. Составить уравнение кривой, для каждой точки которой расстояния от начала координат и от точки  относятся как 3:2. Сделать чертеж.
относятся как 3:2. Сделать чертеж.
Задание 4. Дана функция  на отрезке
на отрезке  . Требуется:
. Требуется:
1) построить график функции в полярной системе координат по точкам, давая 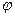 значения через промежуток
значения через промежуток 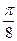 , начиная от
, начиная от  ; 2) найти уравнение линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс - с полярной осью; 3) по полученному уравнению определить, какая это будет линия; 4) сделать чертеж.
; 2) найти уравнение линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс - с полярной осью; 3) по полученному уравнению определить, какая это будет линия; 4) сделать чертеж.
1. 
 2.
2. 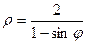
3.  4.
4. 
5. 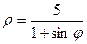 5.
5. 
7.  8.
8. 
9. 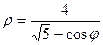 10.
10. 
Задание 5. Дано комплексное число  . Требуется: 1) записать число
. Требуется: 1) записать число  в алгебраической и тригонометрической формах; 2) найти все корни уравнения
в алгебраической и тригонометрической формах; 2) найти все корни уравнения 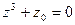 .
.
1.  2.
2. 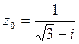
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 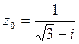
9. 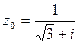 10.
10.