Алгоритм топологической сортировки

Алгоритм генерирует последовательность согласованных меток для вершин бесконтурного орграфа G = (V, Е).В самом начале работы алгоритма антецеденты каждой вершины v записываются в множество A(v). Алгоритм успешно присваивает метки вершинам. Каждая вершина получает очередную метку в том случае, если у нее нет неотмеченных антецедентов.

Пример 2.Найдите последовательность меток для орграфа, изображенного на рис. 4.31.

Решение.

Шаг ОМножество антецедентов выглядит следующим образом: A(А) = {В}, А(В) = {С}, А(С) = {Н}, A(D) = {С}, A{Е) = {D,G},A(F) = {E}, A(G) = {С} и А(Н) =Ø.

Шаг 1Назначить метку 1 вершине Н и удалить вершину Н из всех оставшихся множеств A(v). А(A) = {В}, А(В) = {С}, А(С) = 0, A(D) = {С}, А(E) = {D,G}, A(F) = {Е} и A(G) = {С}.

Шаг 2Назначить метку 2 вершине С и удалить вершину С из всех оставшихся множеств A(v). A(А) = {В}, A(В)= Ø, A(D)= Ø, A(Е) = {D,G}, A(F)= {Е} и A(G) = Ø.

Шаг 3Теперь у нас появился выбор: какой вершине присвоить очередную метку? В зависимости от нашего выбора, получатся разные последовательности меток. Присвоим, например, метку 3 вершине В, и удалим В из множеств A(v). А(А) = Ø, A(D) = Ø, A(Е) = {D, G}, A(F) = {Е} и A(G) = Ø.

Шаг 4 Мы снова стоим перед выбором.Назначим метку 4 вершине А и удалим вершину А из A(u). A(D) = Ø, А(Е) = {D,G}, A(F) = {Е} и A(G) = Ø.

Шаг 5Назначим метку 5 вершине D и удалим вершину D из A(u). А(Е) = {G}, A(F) = {Е} и A(G) = Ø.

Шаг 6Назначим метку 6 вершине G и удалим вершину G из A(u). A(E) = Ø, и A(F) = Ø.

Шаг 7Назначаем метку 7 вершине Е и удаляем Е из списка A(u). Останется только A(F) = Ø.

Шаг 8 Назначаем метку 8 вершине F.

Итак, один из возможных приоритетных списков: Н, С, В, А, D, G, E, F. Он дает нам порядок, в котором можно изучать курсы, соблюдая должную последовательность.

Пути в орграфах

Ориентированные графы успешно применяются для схематичного изображения аэролиний, соединяющих города всего мира, или коммуникационных сетей между компьютерами. В таких сетях важно знать последовательность выключений любого соединения (дуги или вершины) по всей сети.

Например, если самолет не может приземлиться для дозаправки в некотором городе вследствие неблагоприятных погодных условий, то ошибка в его переадресации грозит катастрофой: ему может не хватить горючего для достижения неправильно назначенного аэропорта. Аналогично, если одна или несколько цепей в компьютерной сети не работают, то для некоторых пользователей отдельные серверы могут оказаться вообще недоступными.

Таким образом, мы приходим к задаче о поиске путей между произвольной парой вершин в ориентированном графе.

Пусть G = (V, Е) — орграф с n вершинами, а М — его матрица смежности. Напомним, что буквой И на пересечении i-той строки и j-гo столбца мы обозначаем наличие дуги от вершины с номером i к вершине с номером j. Дуга, по определению, является путем длины 1. Булево произведение матрицы М с самой собой обозначается через M ². В этой матрице буква И символизирует наличие пути длины 2. По матрице M ³ = М ^. М ^. М можно определить все пути длины 3, и вообще, матрица М^k хранит сведения о путях длины k. Наконец, в матрице достижимости

М* = М или М ² или ... или М ⁿ

записаны пути любой длины между вершинами.

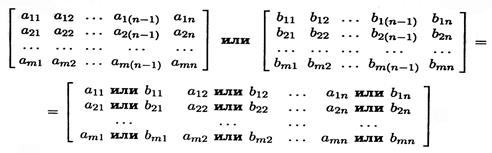
Если у нас есть две логические матрицы одного размера, то в результате логической операции или получится матрица, чьи элементы — результат применения этой операции к соответствующим элементам двух данных матриц. Более точно,

Матрица достижимости орграфа G = (V, Е) фактически является матрицей замыкания по транзитивности Е* отношения Е на вершинах орграфа G.

Пример 3. Вычислите матрицу достижимости орграфа, представленного на рис. 4.32.

Решение. Прежде всего, напишем матрицу смежности орграфа.

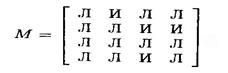
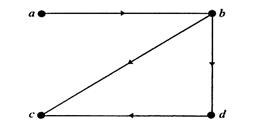
Рис. 4.32.

Квадрат матрицы М равен:

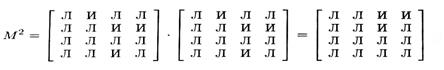
Заметим, что буква И в матрице М² соответствует путям длины 2 в орграфе G, а именно: abc, abd и bdc.

Дальнейшие вычисления приводят к третьей и четвертой степеням матрицы М.

Следовательно,

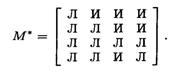
Отметим, например, что буква И в верхнем правом углу матрицы М^* появляется из матрицы М² и соответствует пути abd.

Для больших орграфов вычисление матрицы М* с помощью возведения М все в большую степень утомительно и неэффективно.

Более удобный путь определения М* дает так называемый алгоритм Уоршелла. Пусть G = (V, Е) — орграф с вершинами u₁, u₂, ..., u_n. Алгоритм Уоршелла генерирует последовательность матриц W₀ = М, W₁, W₂…, W_n, причем элемент матрицы W_k (к ≥1), стоящий на пересечении i-ой строки и j-ro столбца W_k(i, j), равен И в том и только том случае, когда существует путь (произвольной длины) из вершины u_i в вершину u_j с внутренними вершинами из множества {u₁, u₂, ..., u_k}. Матрица W_o совпадает с матрицей смежности М орграфа, а W_n — искомая матрица достижимости М*.

Для лучшего понимания работы алгоритма Уоршелла, необходимо с его помощью вручную вычислить матрицу достижимости какого-нибудь орграфа. За каждый проход цикла (пронумерованный индексом к) алгоритм Уоршелла генерирует матрицу W_k , используя элементы предыдущей матрицы W_k-₁.

Чтобы найти i-ую строку матрицы W_k , нам следует вычислить выражения:

W_k-1(i,j)) или(W_k-1(i, k) иW_k-1(k, j)) (1)

при разных значениях j.

Если W_k-1(i, к) = Л, то (W_k-1(i, k;) иW_k-1(k, j)) = Л, и значение выражения (1) совпадает со значением W_k-1(i, j). Иначе говоря, i-ая строка матрицы остается неизменной. В том же случае, когда W_k-1(i, к) = И, вычисление выражения (1) сводится к вычислению (W_k-1(i, к) иW_k-1(k, j)). При этом i-ая строка получается с помощью логической операции илииз текущей строки i и текущей строки k. Говоря более аккуратно, при вычислении W_k поступают следующим образом.

1. Берем k-ый столбец матрицы W_k-1.

2. Строку с номером I (i= 1, ..., п), у которой на k-ом месте стоит Л, переписываем в i-ую строку матрицы W_k .

3. Строку с номером i(i=1, ..., п), у которой на k-ом месте стоит И, спариваем с помощью операции илис k-ой строкой, а результат записываем в i-ую строку матрицы W_k.

Пример 4.С помощью алгоритма Уоршелла вычислите матрицу достижимости орграфа, изображенного на рис. 4.33

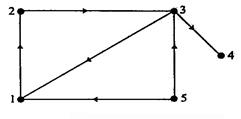
Рис. 4.33

Решение.Матрица W₀ совпадает с матрицей смежности данного орграфа.

Теперь вычисляем W₁. Учитывая первый шаг, мы рассматриваем 1-ый столбец матрицы W₀. Следуя указаниям шага 2, скопируем строки матрицы W₀ с номерами 1, 2 и 4 в матрицу W₁ на те же места. Таким образом,

Далее, согласно шагу 3, строка с номером 3 матрицы W₁ получается с помощью логической операции илииз 1-ой и 3-ей строк матрицы W₀. Поэтому

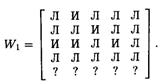
Опять применяем шаг 3 алгоритма для вычисления 5-ой строки матрицы W₁ с помощью операции или, примененной к 5-ой и 1-ой строкам матрицы W₀. Получаем

Матрица W₁ вычислена. Теперь строим матрицу W₂, по матрице W₁. Взгляд на 2-ой столбец матрицы W₁ показывает, что строки с номерами 2 и 4 копируются в W_2. Первая строка матрицы W₂ - результат применения операции или к 1-ой и 2-ой строкам из W₁. Третья строка в W₂ получается спариванием 3-ей и 2-ой строк матрицы W₁. И, наконец, пятая строка W₂ — результат логической операции или, примененной к 5-ой и 2-ой строкам W₁. Значит,

Отметим, в частности, что на пересечении 3-ей строки и 3-го столбца матрицы W₂ стоит буква И. Это означает, что существует контур, начинающийся и заканчивающийся в вершине 3, проходящий через одну или обе вершины с номерами 1 и 2. Посмотрев на изображение орграфа (рис. 4), убеждаемся, что действительно существует контур длины 3: 3123.

Аналогичным образом вычисляется матрица W₃.

Поскольку из вершины 4 не выходит ни одной дуги, то мы не сможем построить ни одного пути, проходящего через вершину 4. Следовательно, матрица W₄ совпадает с W₃. Кроме того, в орграфе отсутствуют дуги, ведущие в вершину 5. Значит, нет и путей, через нее проходящих, т.е. W₅ = W₄. Наконец, W₅ = М*, поскольку граф

Кратчайший путь

Рассмотрим задачу поиска кратчайшего пути, связывающего пару данных вершин в нагруженном орграфе. Слово «кратчайший» здесь вполне уместно, поскольку довольно часто веса в орграфе — это расстояния между пунктами.

Типичная ситуация, которая моделируется нагруженным орграфом, это транспортная сеть (по которой товары доставляются из города в город) и коммуникационная сеть (по которой переправляется информация).

Рассмотрим нагруженный граф на рис. 4.34. Он может представлять, например, длины дорог в милях между шестью деревнями. Поскольку количество вершин в этом графе невелико, то перебрать все возможные пути между любой парой заданных вершин нам вполне по силам. При этом, естественно, мы найдем наиболее короткий путь, соединяющий соответствующие деревни. В реальной задаче, возникающей в профессиональной деятельности, число вершин, как правило, настолько велико, что такой упрощенный подход к поиску кратчайшего пути слишком неэффективен.

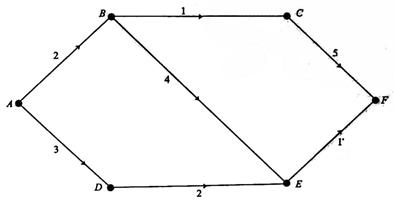
Рис. 4.34. Нагруженный граф

Существует множество алгоритмов поиска кратчайшего пути, но мы познакомимся только с одним, алгоритмом Дейкстры.

Перед формальным изложением алгоритма мы опишем его действия и проиллюстрируем работу алгоритма на нашем примере. Допустим, что нужно найти кратчайший путь от вершины А к любой другой вершине орграфа (см. рис. 8.5). Кратчайший путь — это путь минимального общего веса, соединяющий выбранные вершины. Общий вес, по определению, равен сумме весов всех дуг, составляющих путь. Общий вес кратчайшего пути, ведущего из вершины и в вершину v , называют расстоянием от и до v.

Определим весовую матрицу w, чьи элементы w(u, v) задаются формулой

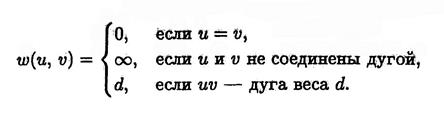
Для нашего графа весовая матрица выглядит следующим образом:

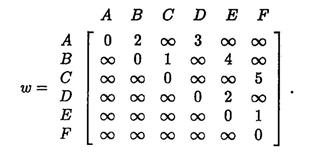
В течение работы алгоритма каждой вершине v орграфа присваивается число d[v], равное расстоянию от вершины А до v. Перед началом работы d[v] совпадает с весом дуги (A, v), если такая существует, или равно ∞ в противном случае. Мы будем проходить вершины орграфа и уточнять значения d[v].

На каждом шагу алгоритма отмечается одна вершина и, до которой уже найден кратчайший путь от A и расстояние d[u] до нее. Далее полученное значение d[u] отмеченной вершины не меняется. Для оставшихся, неотмеченных вершин v, число d[v] будет меняется с учетом того, что искомый кратчайший путь до них от А будет проходить через последнюю отмеченную вершину и. Алгоритм завершится в тот момент, когда все возможные вершины будут отмечены и получат свои окончательные значения d[v].

Для каждого шага алгоритма, описанного ниже, в соответствующую строку табл. 4.6 заносится отмеченная вершина, текущие значения d[v] и оставшиеся неотмеченные вершины. При этом полужирным шрифтом выделяется наименьшее из значений d[v] среди неотмеченных вершин. Соответствующую вершину следует отметить. Кроме того, в таблице все значения d[v] для уже отмеченных вершин отделены от остальных ломаной линией.

Таблица 4.6

Шаг	Отмеченные вершины	Расстояние до вершины	Неотмеченные вершины
А	B	C	D	E	F
	A		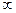		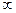		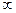	B,C,D,E,F,
	B		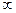					C,D,E,F
	C		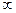					D,E,F
	D		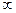					E,F
	E							F
	F

Шаг 0 Поскольку мы интересуемся кратчайшими путями от вершины А, мы ее отмечаем и используем первую строку весовой матрицы w для определения начальных значений d[v]. Таким образом, получается первая строка таблицы. Наименьшее число из всех d[v] для неотмеченных вершин — это d[B] = 2.

Шаг 1 Отмечаем вершину В, так как она является ближайшей к А. Вычисляем длины путей, ведущих от A к неотмеченным вершинам через вершину В. Если новые значения d[v] оказываются меньше старых, то меняем последние на новые. Итак, при этом проходе цикла путь ABC имеет вес 3, а путь ABE — 6, в то время как старые расстояния до этих вершин от А были ∞. Следовательно, заполняя вторую строку таблицы, мы заменим d[C] на 3 и d[E] на 6.

Шаг 2 Из оставшихся неотмеченными, вершины С и D находятся ближе всех к А. Отметить можно любую из них. Возьмем вершину D. Так как длина пути ADE равна 5, текущее значение d[E] следует уменьшить до 5. Теперь можно за­полнить третью строчку таблицы. Наименьшее значение d[v] среди неотмеченных к этому моменту вершин оказывается у вершины С.

Шаг 3 Отмечаем вершину С и подправляем значения d[v]. Теперь можно дойти и до вершины F, следуя путем А В C F. Его длина, а стало быть и значение d[F], равны 8. К этому моменту остались неотмеченными две вершины: Е и F.

Шаг 4 Мы отмечаем вершину Е, что позволяет нам уменьшитьвеличину d[F] с 8 до 6.

Шаг 5 Отмечаем вершину F.

Алгоритм Дейкстры

Алгоритм Е. Дейктры основан на двух идеях:

1. Присваивании вершинам графа временных и окончательных меток и формулировке правила пересчета этих меток (пересчет меток называется релаксацией ребер); при этом окончательные метки и есть длины кратчайших путей;

2. Использовании экстремального свойства кратчайшего пути: если кратчайший путь из вершины х в вершину y проходит через вершину z, то его отрезок от вершины х до вершины z является кратчайшим путем от вершины х до вершины z, а его отрезок от вершины z до вершины у является кратчайшим путем от вершины z до вершины у.

Алгоритм поиска кратчайшего пути, начиная от вершины s, просматривает граф, помечая вершины x_i значениями-метками их расстояний от вершины s. Временная метка x_i – это минимальное расстояние от вершины s к вершине x_i , когда в определении пути на графе учитываются не все маршруты между этими вершинами.

Алгоритм Дейкстры решает задачу о кратчайших путях от фиксированной вершины для взвешенного орграфа G=(V,E), в котором веса всех дуг неотрицательны, ко всем остальным вершинам графа. В процессе работы алгоритма поддерживается множество 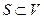, состоящее из вершин v, для которых расстояние d(s,v) уже найдено. Алгоритм выбирает вершину u из очереди T = V \ S с наименьшим расстоянием d(s,v) добавляет вершину u к множеству S и производит пересчет меток всех вершин из очереди Т, с которыми связаны вершины из множества S, в цикле до тех пор, пока очередь Т не станет пустой. При этом в цикле новые вершины в очередь не добавляются и каждая вершина, удаляемая из очереди Т, добавляется к множеству S лишь один раз. Таким образом, число итераций (шагов) в цикле равно мощности множества вершин .

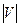Текущее состояние вычислительного процесса состоит в том, что все множество вершин графа фактически разбивается на три подмножества:

- S – множество вершин, расстояние до которых уже вычислено; вначале это множество состоит из одной начальной вершины;

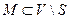- – множество вершин, расстояние до которых вычисляется ;

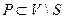- – множество вершин, расстояние до которых будет вычислено.

Алгоритм Дейкстры состоит в следующем:

Шаг 0. Начальное состояние. Обозначим через s начальную вершину, а через m(s) – метку произвольной вершины х. Вначале вершине s присваивается окончательная метка 0 (нулевое расстояние до самой себя), т.е. m(s)=0, а всем остальным вершинам присваивается временная метка 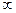. Кроме того, полагаем 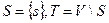. Здесь под метками подразумевается некоторое расстояние (длина пути) от начальной вершины до других вершин 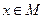, , 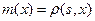при этом .

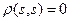Шаг 1. Правило пересчета меток. Пересчитываются только те метки вершин 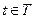, для которых существуют дуги, ведущие из вершин 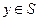, по формуле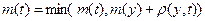

Шаг 2. Изменение множеств (массивов) S и T. Из вершин, метки которых были пересчитаны, выбираем вершину t, имеющую наименьшую метку, и находи множества 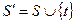и .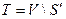

Шаг 3. Условие выхода из цикла. Если 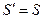, то нужно перейти к следующему шагу 4, в противном случае нужно выполнить присваивание: 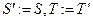и перейти к шагу 1.

Шаг 4. Величина m(s) – длина кратчайшего пути из вершины s в вершину х. Если 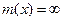, то пути из вершины s в вершину х на графе не существует.

Пример 5. Для орграфа, заданного на рисунке 4.35., найти длины кратчайших путей от вершины s ко всем остальным вершинам и восстановить кратчайшие пути к ним. Проиллюстрировать выполнение алгоритма Дейкстры с помощью последовательности рисунков графа так, чтобы было видно, как выбирается вершина для очередной итерации.

Решение: Сведем решение задачи в табл. 4.7, окончательные метки в которой выделены полужирным шрифтом.

Таблица 4.7

Номер шага перерасчета меток	Множество S	Очередь	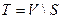s	x	y	u	v
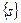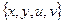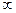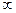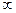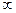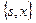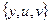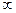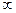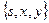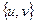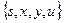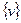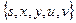		Ø

Длины кратчайших путей от вершины s до остальных вершин будут равны , , , .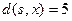

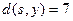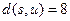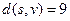Кратчайшие пути будут соответственно равны:

;

;

;

.

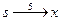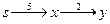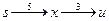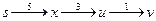Восстановление кратчайших путей происходит в обратном порядке.

На следующем рисунке приведена графическая иллюстрация алгоритма Дейкстры. Исходная вершина – крайняя левая. Вершины закрашенные черным цветом, лежат в множестве S, остальные вершины находятся в очереди 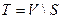. Вершина, заштрихованная серым цветом имеет минимальную метку и выбирается в качестве очередной вершины при следующей итерации. Утолщенные дуги образуют деревья кратчайших путей с корнем в исходной вершине s на каждом шаге итерации. При окончании алгоритма мы получим полное дерево кратчайших путей с корнем в вершине s.

При реализации алгоритма Дейкстры на ЭВМ граф представляется матрицей весов дуг, соединяющих вершины. Матрица весов является простым обобщением матрицы смежности графа.

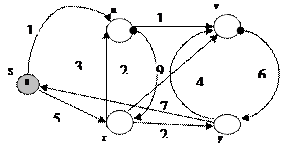
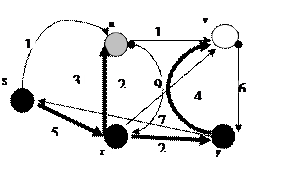
Рис. 4.35. Графическая реализация алгоритма Дейкстры.

Контрольные вопросы.

1. Что представляет собой орграф? В каких случаях они применяются?

2. Что в орграфе называется антецедентом?

3. Дать определение пути и контура в орграфе.

4. Какой граф называют бесконтурным? Пояснить случаи их применения и дать их кодовое название.

5. Что такое последовательность согласованных меток?

6. Рассказать смысл алгоритма топологической сортировки.

7. Что называется матрицей достижимости и что она характеризует?

8. Рассказать об алгоритме Уоршелла.

9. Как осуществляется поиск кратчайшего пути.

10. Пояснить смысл алгоритма Дейкстры и перечислить его структуру.

11. Что называется весовой матрицей и где и для чего она определяется?

12. Что называется полустепенью исхода и полустепенью захода вершины?

13. Дать определение связного орграфа.