Численное решение алгебраических уравнений. Метод бисекций

Раздел 4. ЧИСЛЕННЫЕ МЕТОДЫ

Вычислительной математикой называют раздел математики, в котором изучаются методы решения математических задач путем реализации вычислительных алгоритмов, а также круг вопросов, связанных с организацией и проведением вычислений. Указанные методы принято называть численными методами. Для выяснения понятия численного метода рассмотрим следующую задачу: найти действительные корни уравнения:

.

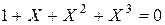Замечаем, что левая часть уравнения является суммой элементов геометрической прогрессии и может быть преобразована следующим образом:

.

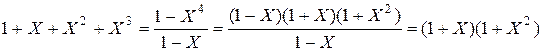Теперь уравнение записывается в виде

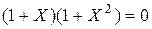
и очевидно имеет единственный действительный корень 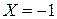. В данной задаче использован аналитический метод решения, основанный на использовании аналитического аппарата: формул, теорем, преобразований и т.п.

Решим теперь похожее уравнение

.

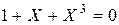После нескольких безрезультатных попыток аналитического решения исследуем уравнение графическим методом.

Построив примерный график функций 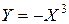и (см. рис. 1), видим, что они пересекаются в единственной точке.

Абсцисса точки пересечения указывает приближенное значение корня уравнения .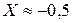

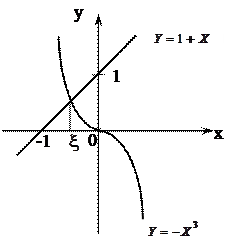Рис. 1.

Приближенное расположение корня можно установить еще следующим образом. Вычисляем значения функции, стоящей в левой части уравнения, в целочисленных точках и результаты сводим в таблицу

X	-1
1 +X +X3	-1

Непрерывная функция принимает все значения между своими значениями на концах интервала. Поэтому, очевидно, корень уравнения 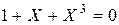лежит на интервале (-1; 0). Если в качестве решения задачи взять середину интервала, то можно сказать, что корень уравнения приближено равен -0,5 и отстоит от точного значения на величину, не превышающую 0,5. Абсолютную величину отклонения найденного приближенного решения от точного значения назовем погрешностью решения задачи. Тогда 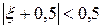и погрешность в определении корня меньше 0,5.

Уточним место расположения корня, для чего вычислим функцию при 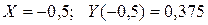. Из сравнения 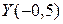со значениями функции на концах интервала (-1;0) видим, что вследствие разности знаков функции корень уравнения расположен на интервале (-1; -0,5). Середину данного интервала 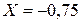считаем новым приближенным значением корня. При этом погрешность не превышает 0,25. Повторяем процесс вычислений до тех пор, пока величина погрешности не станет удовлетворительной.

Рассмотренный метод решения уравнений относится к численным методам и называется методом бисекций. В нем значение корня находится с заранее договоренной погрешностью путем вычисления и анализа последовательности значений функции. Вычисления производятся в определенной последовательности и остаются однотипными для любого вида уравнения.

Пусть методом бисекций решается уравнение 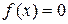и z-точное значение корня уравнения. Первоначально путем исследования поведения функции 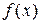определим интервал расположения корня уравнения. Предположим это будет интервал , для которого . Принимаем середину интервала 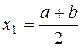за приближенное значение корня и сравниваемполовину длины интервала 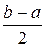с допустимой погрешностью 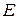. При 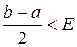решение задачи заканчивается. В противном случае вычисляем и делаем выбор, какую из двух половин интервала взять для дальнейшего уточнения корня. Процесс вычислений циклически повторяется с последовательным сокращением в два раза ширины интервала расположения корня на каждом последующим цикле. После циклов достигается погрешность меньшая 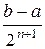.