Замкнутые классы функций
Множество Млогических функций называется замкнутым классом, если любая суперпозиция функций из М снова принадлежит М.
Всякая система функций алгебры логики порождает замкнутый класс - класс, состоящий из функций, которые можно получить суперпозициями из М.Такой класс называется замыканием Ми обозначается [М].Очевидно, что если М - замкнутый класс, то [М]=М.ЕслиМ - полная система функций, то [М]=  , где
, где  -множество всех функций алгебры логики.
-множество всех функций алгебры логики.
Монотонные функции. Теорема о монотонных функциях.
Функция алгебры логики  ,называется монотонной,если для любых n мерных двоичных наборов
,называется монотонной,если для любых n мерных двоичных наборов  ,из того, что
,из того, что  , следует, что
, следует, что  .
.
Теорема о монотонных функциях.
Всякая булева функция в сигнатуре алгебры логики, не содержащая отрицаний, является монотонной функцией.
Для любой монотонной функции алгебры логики, отличной от 0 и 1, найдется равносильная ей булева функция без отрицаний.
Доказательство первой части теоремы основано на рассмотрении ДНФ, равносильной исходной функции без отрицаний. Для произвольного двоичного набора, на котором значение ДНФ равно 1, найдется элементарная конъюнкция, которая на этом наборе равна 1. Так как в этой конъюнкции нет отрицаний, то это означает, что все компоненты набора равны 1. Тогда на любом другом большем или равном наборе значение элементарной конъюнкции тоже будет равно 1, а тем самым выполняются условия монотонности.
Доказательство второй части теоремы основано на рассмотрении СДНФ, равносильной исходной монотонной функции, и предположении, что в ней существует полная правильная элементарная конъюнкция, содержащая хотя бы одну переменную с отрицанием. Тогда исходя из монотонности функции, а тем самым и СДНФ, найдется другая элементарная полная правильная коньюнкция, которая отличается от найденной лишь тем, что переменная, входящая в первую конъюнкцию с отрицанием, входит во вторую без отрицания. Таким образом от исходной СДНФ можно перейти к ДНФ, в которой мы избавились от одной переменной, входящей в СДНФ с отрицанием. Так для всех переменных с отрицаниями.
Следствие из теоремы.
Класс монотонных функций является замыканием системы функций М={&,V,0,1}.
Двойственность в алгебре логики. Самодвойственные функции.
Определение.
Функция  называется двойственнойфункцией к функции
называется двойственнойфункцией к функции .
.
Функция  называется самодвойственной, если
называется самодвойственной, если 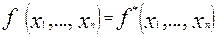 .
.
Самодвойственными являются функции x,  .
.
Функции сохраняющие константы 0, 1.
Определения.
Функция ,для которой выполняется
,для которой выполняется  ,называется функцией, сохраняющей константу 0.
,называется функцией, сохраняющей константу 0.
Функция  ,для которой выполняется
,для которой выполняется  ,называется функцией, сохраняющей константу 1.
,называется функцией, сохраняющей константу 1.
