Леммы Жордана. Несобственные интегралы по действительной оси от функций
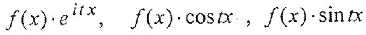
(Лемма Жордана). Если f(z)ÎC¥(Imz>0. z1,z2,...,zN¹¥) и f(z)=>0 при |z|®¥(равномерно по argz , Imz>0), то при ReZ>0
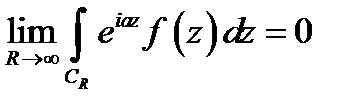 CR - полуокружность |z|=R Imz>0.
CR - полуокружность |z|=R Imz>0.
Пусть R(x) - рациональная функция, не имеющая особых точек на действительной оси, для которой точка z, равная бесконечности, - нуль порядка не ниже первого.
Тогда справедливы формулы:
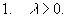
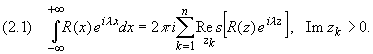
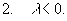
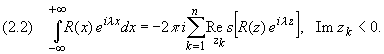
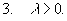
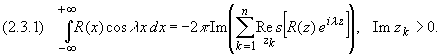
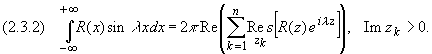
Преобразование Лапласа. Условия на функцию - оригинал.
Пусть имеем функцию действительного переменного f(t), которая удовлетворяет следующим условиям:
1) f(t) однозначна и непрерывна вместе со своими производными n-го порядка для всех t, кроме тех, где она и ее производные имеют разрывы 1-го рода. При этом в каждом конечном интервале изменения t имеется конечное число точек разрыва;
2) f(t)=0для всех t<0;
3) f(t) возрастает медленнее некоторой экспоненциальной функции 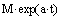 , где М и а- некоторые положительные величины, т.е. всегда можно указать такие М и а, чтобы при любом t>0 соблюдалось неравенство
, где М и а- некоторые положительные величины, т.е. всегда можно указать такие М и а, чтобы при любом t>0 соблюдалось неравенство 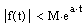 .
.
В операционном исчислении функции f(t) ставится в соответствие новая функция F(p), определяемая равенством
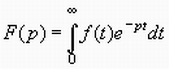
Где p - положительное действительное число или комплексное число с положительной действительной частью.
Функция f(t) при этом называется оригиналом, а F(p)- изображением функции f(t) по Лапласу.
Теорема о существовании изображения и следствие из нее.


41* Второй метод исследования устойчивости Ляпунова. основные определения теории устойчивости. Т. об ассимптотичной устойчивости.
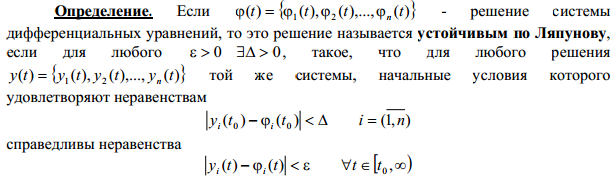
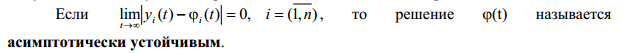

Изображения единичной функции, показательной, степенной, тригонометрических и гиперболических функций.
Нах-е изображения по оригиналу и наоборот наз-ся операц-м исчислением.
1.Ф-я Хевисайда 1(t)= 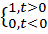
F(p)= 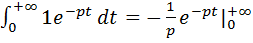 =
=  , Rep
, Rep 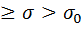 ; 1(t)
; 1(t) 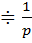

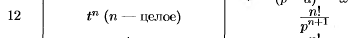
Линейность преобразования Лапласа, теоремы смещения и запаздывания
Линейность - Если f(t), g(t) - функции-оригиналы, имеющие изображения F(p), G(p), то их линейная комбинация α f (t) + β g (t) (α = cost, β = const)- тоже функция-оригинал, и α f (t) + β g (t) 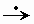 α F(p) + β G(p) .
α F(p) + β G(p) .
ТЕОРЕМА (смещения):Если f(t)≑F(p), то 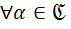 выполняется
выполняется 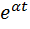 f(t)≑F(p-
f(t)≑F(p- 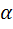 )
)
Смещение в области оригинала
Пусть f(t)- оригинал, тогда ф-я f(t-a) также яв-ся оригиналом с аргументом, запаздыв. на величину a. График ф-и f(t-a) не меняя своей формы получается из графика ф-и f(t) путем сдвига на a ед-ц вправо вдоль оси t.
ТЕОРЕМА (запаздывания): Пусть F(t) имеет изобр.F(p), a>0, тогда f(t-a)≑ 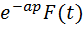
Теорема подобия. Изображение периодического оригинала. Свертка оригиналов. Изображение свертки оригиналов
Если f(t)≑F(p) и 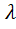 >0, то f(λt)≑
>0, то f(λt)≑ 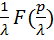
Изображение периодического оригинала
ТЕОРЕМА: Если f(t)- оригинал с периодом T>0, то F(p)= 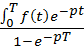
Изображение свертки оригиналов
Сверткой 2х ориг-в 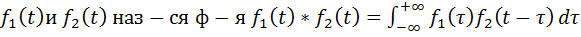
Так при 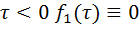 ,
, 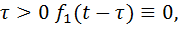 то для свертки получаем след. выр-е:
то для свертки получаем след. выр-е:
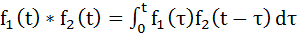
ТЕОРЕМА (Борель): Если 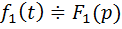 ,
, 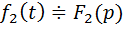 ,то
,то 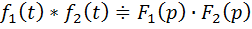
Это равенство наз-ся ф-й умнож-я изоб-й
