Линейные ДУ 1-го порядка. Уравнения Бернулли
Линейное ДУ 1-го порядка: y’+p(x)y=g(x)
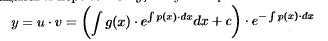 общее решение
общее решение
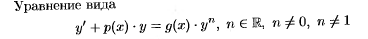 Ур. Бернулли
Ур. Бернулли
При n=0 –линейное, при n=1 – с разделяющимися переменными.
Уравнения в полных дифференциалах
P(x;y)dx+Q(x;y)dy=0 называется уравнением в полных дифференциалах если его левая часть есть полный дифференциал некоторой функции u(x;y), т.е. P(x;y)dx+Q(x;y)dy=du(x;y). В этом случае ДУ можно записать в виде du(x;y)=0, а его общий интеграл будет u(x;y)=с. Для того чтобы выражение P(x;y)dx+Q(x;y)dy, где функции P(x;y) и Q(x;y) и их частные производные 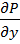 и
и 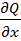 непрерывны в некоторой области D, было полным дифференциалом, необходимо и достаточно выполнение условия:
непрерывны в некоторой области D, было полным дифференциалом, необходимо и достаточно выполнение условия: 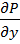 =
= 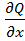 .
.
Интегрирующий множитель
Функция μ(x;y) называется интегрирующим множителем для уравнения P(x;y)dx+Q(x;y)dy=0, если уравнение μ(x;y)P(x;y)dx+μ(x;y)Q(x;y)dy=0 есть уравнение в полных дифференциалах. Интегрирующий множитель удовлетворяет уравнению 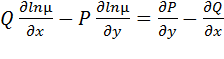
Если 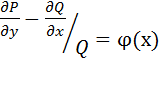 (не зависит от y), то
(не зависит от y), то 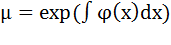 . Если
. Если 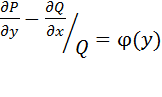 (не зависит от x), то
(не зависит от x), то 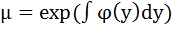 .
.
ДУ высших порядков, задача Коши. Общее, частное решение. Теорема о существовании и единственности решения задачи Коши
ДУ порядка выше первого называются ДУ высших порядков. ДУ второго порядка: F(x;y;y’;y’’)=0 или y’’= F(x;y;y’). Общее решение ДУ – функция y= 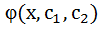 , где
, где 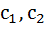 произвольные постоянные. Решение y=
произвольные постоянные. Решение y= 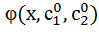 , получающееся из общего решения при конкретных значениях постоянной называется частным решением. Задача нахождения решения ДУ, удовлетворяющего заданным начальным условиям, называется задачей Коши.
, получающееся из общего решения при конкретных значениях постоянной называется частным решением. Задача нахождения решения ДУ, удовлетворяющего заданным начальным условиям, называется задачей Коши.
Если в уравнении y’’= F(x;y;y’) функция F(x;y;y’) и ее частные производные 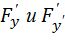 непрерывны в некоторой области D то для всякой точки (x0;y0;y0’) принадлежащей D существует единственное решение y=
непрерывны в некоторой области D то для всякой точки (x0;y0;y0’) принадлежащей D существует единственное решение y= 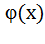 , удовлетворяющее начальным условиям.
, удовлетворяющее начальным условиям.
Уравнения допускающие понижение порядка
Один из методов интегрирования ДУ высших порядков – метод понижения порядка. Суть метода в том, что с помощью замены переменных данное ДУ сводится к ДУ порядок которого ниже. 3 типа уравнения допускающих понижение порядка: y’’=f(x) y’’=f(x, y’) y’’=f(y, y’)
Линейные ДУ высших порядков. Т. о существовании и единственности решения задачи Коши. Т. о св-ве решений ЛОДУ
Ур-е 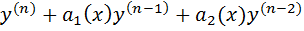 + …+
+ …+ 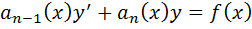 наз-ся ЛНДУ n-го порядка.
наз-ся ЛНДУ n-го порядка.
Если f(x)=0, то ур-е наз-ся ЛОДУ n-го порядка. З.Коши для ЛДУ определяется начальными условиями:
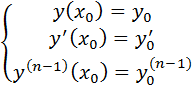
Теорема существования и единственности решения задачи Коши.
Если все коэф-ты 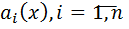 и f(x) непр-ы на [a,b], то на всем этом отрезке сущ-т единственное реш--е з.Коши.
и f(x) непр-ы на [a,b], то на всем этом отрезке сущ-т единственное реш--е з.Коши.
Теорема о свойстве решений линейных однородных дифференциальных уравнений.
1) Если 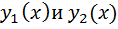 явл-ся реш-ми ЛОДУ, то ф-я
явл-ся реш-ми ЛОДУ, то ф-я 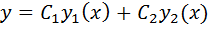 также яв-ся реш-м ЛОДУ при
также яв-ся реш-м ЛОДУ при 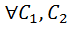
2) Если комплекснозначная ф-я 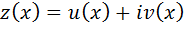 яв-ся реш-м ЛОДУ, то ф-и
яв-ся реш-м ЛОДУ, то ф-и 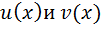 в отдельности также явл-ся реш-и ЛОДУ.
в отдельности также явл-ся реш-и ЛОДУ.
