Дизъюнктивные и конъюктивные нормальные формы
Элементарной конъюнкциейназывается конъюнкция переменных высказываний и (или) их отрицаний.
Элементарной дизъюнкциейназывается дизъюнкция переменных высказываний и (или) их отрицаний.
Обозначим  =x, если
=x, если 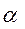 =1 и
=1 и  =
= , если
, если 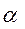 =0.
=0.
Тогда
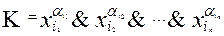 - элементарная конъюнкция,
- элементарная конъюнкция,
 - элементарная дизъюнкция.
- элементарная дизъюнкция.
Дизъюнктивной нормальной формой (ДНФ) данной формулы называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций.
Конъюктивной нормальной формой (КНФ) данной формулы называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.
Для того, чтобы построить по данной формуле алгебры логики равносильную ей ДНФ или КНФ необходимо перейти в сигнатуру алгебры логики (выразить все операции через дизъюнкцию, конъюнкцию и отрицание), воспользоваться законом де Моргана для того, чтобы отрицания стояли лишь над элементарными переменными высказываниями, раскрыть скобки (для построения ДНФ) или воспользоваться дистрибутивным законом (для построения КНФ).
Разложение функций алгебры логики по к переменным. СДНФ и СКНФ.
Представление функции 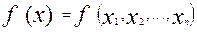 в виде
в виде
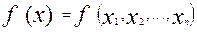 =
= 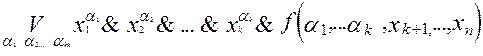 (*)
(*)
называется разложением функции 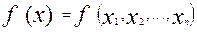 от n переменных по k переменным.
от n переменных по k переменным.
Замечания.
1. 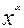 =1 тогда и только тогда, если
=1 тогда и только тогда, если 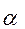 =x.
=x.
2. 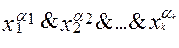 =1,тогда и только тогда, если
=1,тогда и только тогда, если  .
.
Теорема о разложении функции алгебры логики по k переменным.
Всякую функцию алгебры логики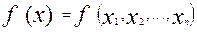 от n переменных можно представить в виде (*).
от n переменных можно представить в виде (*).
Доказательство теоремы основано на том, что выбрав произвольный двоичный n- мерный набор из 0 и 1, можно показать, используя замечание 1, что левая и правая части выражения (*) совпадают.
Следствием из этой теоремы является
Теорема о представлении любой функции алгебры логики в сигнатуре алгебры логики.
Всякая функция алгебры логики может быть представлена в виде формулы, содержащей только операции конъюнкции, дизъюнкции и отрицания.
Совершенные нормальные формы.
Совершенная дизъюнктивная нормальная форма.
Определение 1.
Элементарная конъюнкция называется правильной,если в неё каждая переменная входит не более одного раза, включая её вхлждение и под знаком отрицания.
Определение 2.
Элементарная конъюнкция называется полной относительно переменных x,y,z ..., если в неё входит каждая из этих переменных не менее одного раза, включая и их вхождение под знаком отрицания.
Определение 3.
Совершенной дизъюнктивной нормальной формой (СДНФ) относительно переменных x,y,z,... ,называется дизъюнктивная нормальная форма, в которой нет одинаковых элементарных конъюнкций и все элементарные конъюнкции правильные и полные относительно переменных x,y,z,... .
