Общая схема для построения графиков функций
1. Найти область определения функции 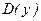 .
.
2. Найти точки пересечения графика функций с осями координат.
3. Исследовать функцию на четность или нечетность.
4. Исследовать функцию на периодичность.
5. Найти промежутки монотонности и точки экстремума функции.
6. Найти промежутки выпуклости и точки перегиба функции.
7. Найти асимптоты функции.
8. По результатам исследования построить график .
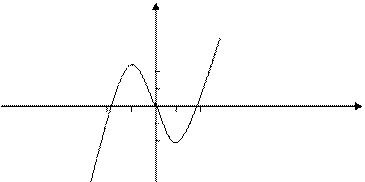
Пример № 1: Исследовать функцию и построить ее график:
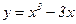 .
.
Решение:
1) Функция определена на всей числовой оси, т. е. ее область определения 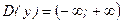 .
.
2) Найдем точки пересечения с осями координат:
с осью ОХ : решим уравнение 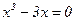
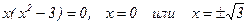 .
.
с осью ОY: 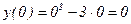
3) Выясним, не является ли функция четной или нечет
ной:
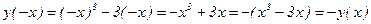 .
.
Отсюда следует, что функция является нечетной.
4) Функция непериодична.
5) Найдем промежутки монотонности и точки экстремума функции: 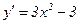 .
.
Критические точки: 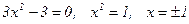 .
.
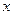 | 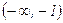 | -1 | 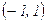 | 1 | 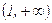 |
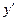 | + | 0 | - | 0 | + |
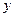 |  | т. max |  | т. min -2 |  |
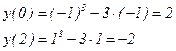
6) Найдем промежутки выпуклости и точки перегиба функции: 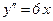
Критические точки: 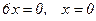 .
.
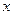 | 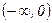 | 0 | 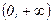 |
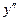 | - | 0 | + |
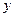 |  | точка перегиба |  |
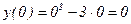
7) Функция непрерывна, асимптот у нее нет.
8) По результатам исследования построим график функции:
 y
y
1 x
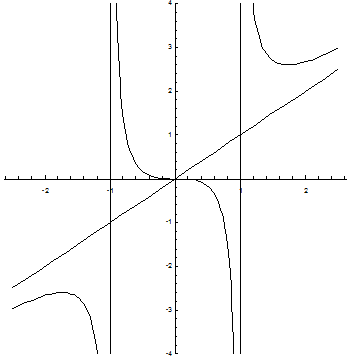
Пример № 2Исследовать функцию 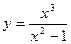 и построить ее график.
и построить ее график.
Находим область существования функции. Очевидно, что областью определения функции является область (-¥; -1) È (-1; 1) È (1; ¥).
В свою очередь, видно, что прямые х = 1, х = -1 являются вертикальными асимптотами кривой.
Областью значений данной функции является интервал (-¥; ¥).
Точками разрыва функции являются точки х = 1, х = -1.
Находим критические точки.
Найдем производную функции
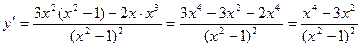
Критические точки: x = 0; x = - 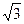 ; x =
; x = 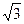 ; x = -1; x = 1.
; x = -1; x = 1.
Найдем вторую производную функции
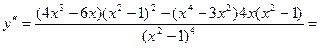
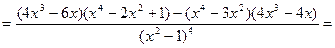
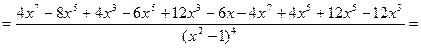
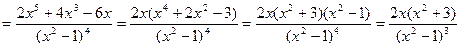 .
.
Определим выпуклость и вогнутость кривой на промежутках.
-¥ < x < - 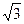 , y¢¢ < 0, кривая выпуклая
, y¢¢ < 0, кривая выпуклая
- 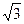 < x < -1, y¢¢ < 0, кривая выпуклая
< x < -1, y¢¢ < 0, кривая выпуклая
-1 < x < 0, y¢¢ > 0, кривая вогнутая
0 < x < 1, y¢¢ < 0, кривая выпуклая
1 < x < 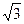 , y¢¢ > 0, кривая вогнутая
, y¢¢ > 0, кривая вогнутая
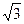 < x < ¥, y¢¢ > 0, кривая вогнутая
< x < ¥, y¢¢ > 0, кривая вогнутая
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
-¥ < x < - 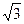 , y¢ > 0, функция возрастает
, y¢ > 0, функция возрастает
- 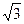 < x < -1, y¢ < 0, функция убывает
< x < -1, y¢ < 0, функция убывает
-1 < x < 0, y¢ < 0, функция убывает
0 < x < 1, y¢ < 0, функция убывает
1 < x < 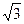 , y¢ < 0, функция убывает
, y¢ < 0, функция убывает
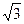 < x < ¥, y¢¢ > 0, функция возрастает
< x < ¥, y¢¢ > 0, функция возрастает
Видно, что точка х = - 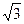 является точкой максимума, а точка х =
является точкой максимума, а точка х = 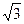 является точкой минимума. Значения функции в этих точках равны соответственно -3
является точкой минимума. Значения функции в этих точках равны соответственно -3 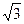 /2 и 3
/2 и 3 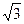 /2.
/2.
Про вертикальные асимптоты было уже сказано выше. Теперь найдем наклонные асимптоты.
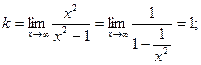
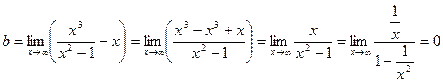
Уравнение наклонной асимптоты – y = x.
Построим график функции: