С.Функция Грина в двумерном и трехмерном случаях
Уравнение теплопроводности. Физический смысл.
Выведем уравнение, описывающие распределение температуры в теле. Пусть 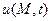 - температура тела в точке М в момент времени t. Будем пользоваться законом Фурье для плотности потока тепла ω в направлении
- температура тела в точке М в момент времени t. Будем пользоваться законом Фурье для плотности потока тепла ω в направлении 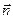 в единицу времени:
в единицу времени: 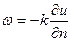 , к – коэффициент теплопроводности, может зависеть от температуры, точки и времени. Рассмотрим часть тела D, ограниченную поверхность S. Пусть
, к – коэффициент теплопроводности, может зависеть от температуры, точки и времени. Рассмотрим часть тела D, ограниченную поверхность S. Пусть 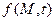 - плотность источников тепла. подсчитаем баланс тепла для D за малое время Δt: Q1=Q2+Q3, где
- плотность источников тепла. подсчитаем баланс тепла для D за малое время Δt: Q1=Q2+Q3, где
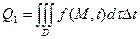 - приход за счёт источников тепла.
- приход за счёт источников тепла.
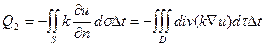 - расход за счёт выходящего из D потока.
- расход за счёт выходящего из D потока.
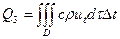 - расход на изменение температуры, где с – коэффициент теплоёмкости, ρ – плотность в-ва.
- расход на изменение температуры, где с – коэффициент теплоёмкости, ρ – плотность в-ва.
Тогда можно записать: 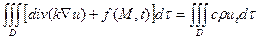 , откуда ввиду произвольности D следует:
, откуда ввиду произвольности D следует:
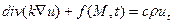 - уравнение теплопроводности.
- уравнение теплопроводности.
Задача Коши с однородным уравнением на прямой
А.Решение с точечным источником.
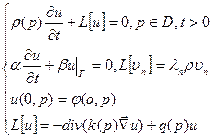 | Решение: 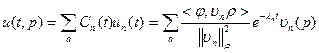 , , 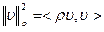 прокомментируем результат: в формуле участвует суммирование по “n” и интегрирование по Д, переставим их: прокомментируем результат: в формуле участвует суммирование по “n” и интегрирование по Д, переставим их: 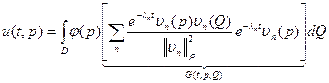 , , |
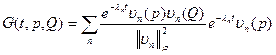 - ядро, функция Грина (функция источника) задачи.
- ядро, функция Грина (функция источника) задачи.
Получим вид функции Грина:
Есть задача: 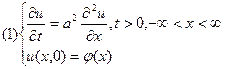 | Рассмотрим частный случай: 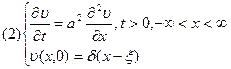 решение этой задачи: решение этой задачи: 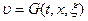 | Проведём замену, при такой замене вид задачи не изменится: 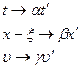 , где , где 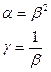 |
Тогда для функции υ можно записать выражение: 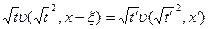 ,т.е. получили функцию одной переменной
,т.е. получили функцию одной переменной 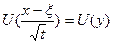 , решение свелось к решению для функции одной переменной
, решение свелось к решению для функции одной переменной 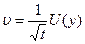 .
.
Подставляем: 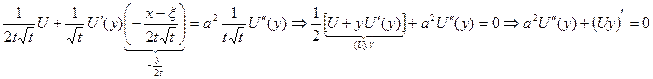
Интегрируем: 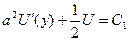 ,
, 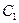 =0, т.к. задача симметрична относительно ξ , чётная функция => производная равна нулю.
=0, т.к. задача симметрична относительно ξ , чётная функция => производная равна нулю.
Интегрируем: 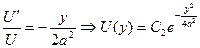 ,
, 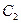 выбираем из условия:
выбираем из условия: 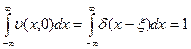 , интегрируем,
, интегрируем, 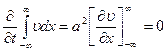 , значит
, значит 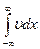 постоянен во времени.
постоянен во времени. 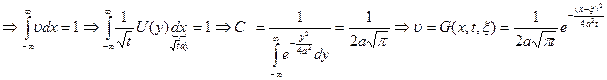
Прокомментируем полученный результат: чтобы понять, что такое функция Грина, рассмотрим следующую задачу:
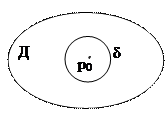 | 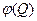 возьмём временно сосредоточенной в некоторой точке р0. Пусть временно: возьмём временно сосредоточенной в некоторой точке р0. Пусть временно: 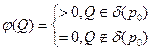 и и 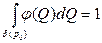 в этом случае решение примет вид: в этом случае решение примет вид: | 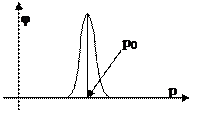 |
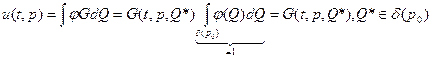
т.е. то решение задачи 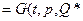 ) в т.
) в т. 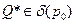 . При
. При 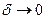
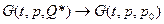
В.Построение решения с известной функцией Грина.
Рассмотрим задачу:
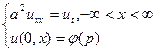 её решение:
её решение: 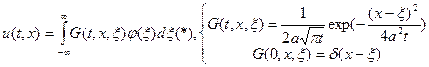
Рассмотрим это решение: 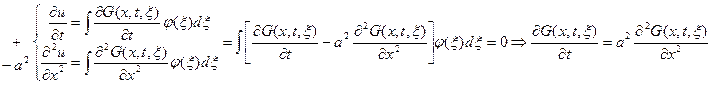 следовательно это решение удовлетворяет уравнению . следовательно это решение удовлетворяет уравнению . 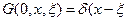 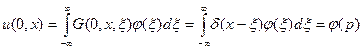 следовательно это решение удовлетворяет начальным условиям. следовательно это решение удовлетворяет начальным условиям. |
Рассмотрим частные случае:
Лемма1: 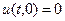 , если
, если 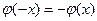 - продлеваем нечётным образом, то решение задачи Коши:
- продлеваем нечётным образом, то решение задачи Коши: 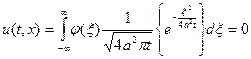 - интеграл от нечётной функции в симметричных пределах.
- интеграл от нечётной функции в симметричных пределах.
Лемма2: 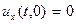 , если
, если 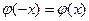 , то
, то 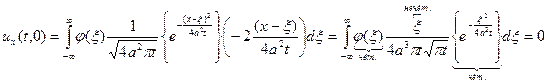
Можно записать для задачи 1:
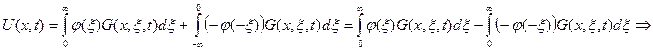
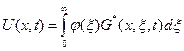 ,
, 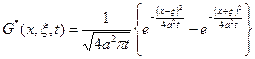 и т.д.
и т.д.
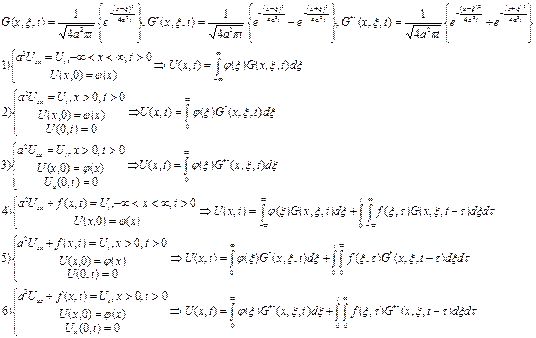
с.Функция Грина в двумерном и трехмерном случаях.
| трёхмерная задача Коши с постоянными коэффициентами: | 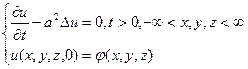 |
Лемма: если 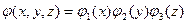 , то
, то 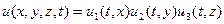 - каждое
- каждое 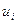 является решением одномерной задачи Коши с соответств. начальными данными.(доказывается подстановкой):
является решением одномерной задачи Коши с соответств. начальными данными.(доказывается подстановкой): 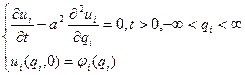
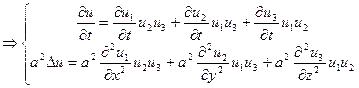
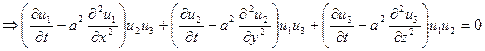
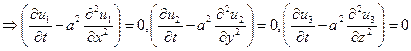 три одномерные задачи, их решения:
три одномерные задачи, их решения:
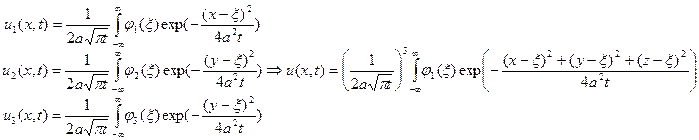
функция Грина в трёхмерном пространстве: 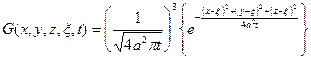 .
.
начальное условие соответствующие трёхмерной задачи.: 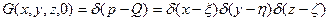
11.Смешанная краевая задача и задача Коши с уравнением 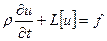 .
.
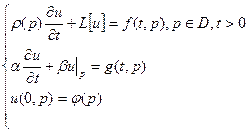 | Разбиваем задачу на три, каждая из которых вызывает одну причину: начальное отклонение, (), внешние силы, т.е. 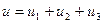 | ||
1) Учитываем граничные условия: подбираем u1 таким, что бы оно удовлетворяло граничным условиям: 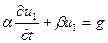 В силу линейности оставшиеся два решения удовлетворяют однородным граничным условиям В силу линейности оставшиеся два решения удовлетворяют однородным граничным условиям | 2) Учитываем начальные условия, не учитываем правую часть: ищем u2 такое, которое удовлетворяет однородному уравнению и однородным граничным условиям, а также получим новые начальные условия: 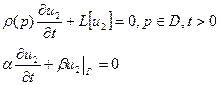 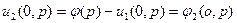 Мы получили однородную задачу для u2 с неоднородными начальными условиями. Её решение в вопросе 8. Мы получили однородную задачу для u2 с неоднородными начальными условиями. Её решение в вопросе 8. | 3) Учитываем начальные условия, не учитываем правую часть: ищем u3 такое, что бы оно удовлетворяло неоднородному уравнению, и получаем для него нулевые условия:. 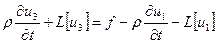 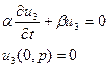 Мы разделили задачу таким образом, что сумм этих трёх частей удовлетворяет исходным уравнению и условиям. Мы разделили задачу таким образом, что сумм этих трёх частей удовлетворяет исходным уравнению и условиям. | |
Рассмотрим все эти задачи по отдельности:
ВОПРОС12а! 2) 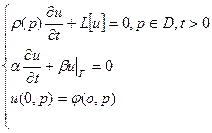 | 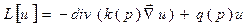 з. Ш.-Л. Задача на собств. знач.: з. Ш.-Л. Задача на собств. знач.: 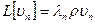 Если решение есть оно должно удовлетворять решению и начальным условиям. Если решение есть оно должно удовлетворять решению и начальным условиям. 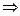 Запишем теорему Стеклова: Запишем теорему Стеклова: 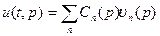 : : | ||
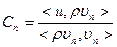 - коэффициенты разложения по ортогональному базису: получили уравнение - коэффициенты разложения по ортогональному базису: получили уравнение 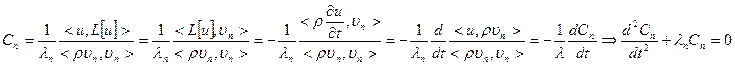 уравнение, которому удовлетворяет Сn. Его общее решение: уравнение, которому удовлетворяет Сn. Его общее решение: 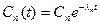 , подставим: , подставим: 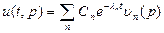 , коэффициенты находим из начальных условий. , коэффициенты находим из начальных условий. 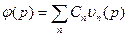 - разложили в ряд по собственным функциям задачи Ш.-Л. - разложили в ряд по собственным функциям задачи Ш.-Л. 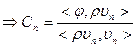 | |||
3) 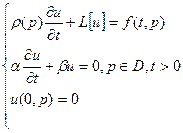 | Воспользуемся т. с. зн. 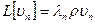 , если решение существует, то , если решение существует, то 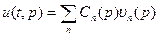 - разложили решение в ряд по собственным значениям, коэффициенты разложения ( - разложили решение в ряд по собственным значениям, коэффициенты разложения ( 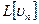 - самосопряженный оператор): - самосопряженный оператор): | ||
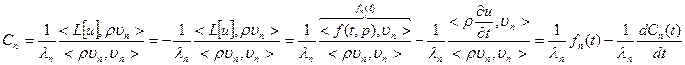 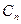 удовлетворяет уравнению: удовлетворяет уравнению: 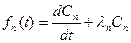 неоднородное линейное дифференциальное уравнение второго порядка, начальные условия получаем исходя из начальных условий задачи. неоднородное линейное дифференциальное уравнение второго порядка, начальные условия получаем исходя из начальных условий задачи. 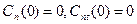 , тогда решение этого уравнения : , тогда решение этого уравнения : 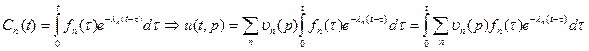 | |||
