Определение значений искомых величин по уравнениям апроксимации и построение графиков

Для определения значений предела прочности и относительного удлинения при температуре 800°С, а также для построения графиков по найденным уравнениям воспользуемся программой Mathcad.

Определение предела прочности при 800°С и построение графика зависимости предела прочности от температуры.

Введем в качестве х значение температуры и вычислим значение предела прочности

при данной температуре по ранее найденному уравнению полиноминальной аппроксимации шестой степени.

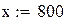
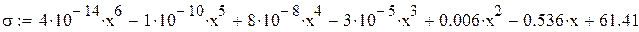
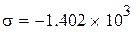
Поскольку полученное значение предела прочности сильно отличается от поученных экспериментальных данных, использовать данное уравнение для расчета и построения графика невозможно. Для определения искомой величины воспользуемся другими уравнениями по мере уменьшения коэффициента корреляции и произведем расчёт для известных данных при температуре 700. Далее будем использовать уравнение полиноминальной аппроксимации четвертой степени с коэффициентом корреляции 0,993. Обозначим предел прочности тем же символом, но добавим числовой индекс, а температуру обозначим буквой у.

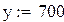
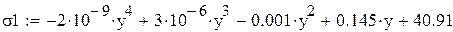
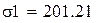
Проверим уравнение полиноминальной аппроксимации третьей степени с коэффициентом корреляции 0,983:

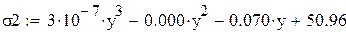
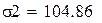
Проверим уравнение полиноминальной аппроксимации второй степени с коэффициентом корреляции 0,972:

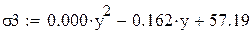
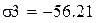
Проверим уравнение степенной зависимости с коэффициентом корреляции 0,741:

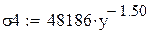
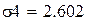
Проверим уравнение логарифмической зависимости с коэффициентом корреляции 0,919:

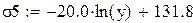
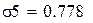
Проверим уравнение экспоненциальной зависимости с коэффициентом корреляции 0,963:

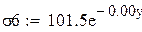
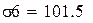
Проверим уравнение линейной зависимости с коэффициентом корреляции 0,893:

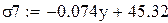
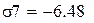
Обозначим температуру символом z, затем строим графики зависимости предела прочности от температуры. Так как значения предела прочности полиноминальной аппроксимации шестой степени σ(z), четвертой σ1(z), третьей σ2(z), второй степени σ3(z) и экспоненциальной зависимости σ6(z) сильно отличаются от экспериментальных значений, то нет смысла строить их графики. Построим графики остальных уравнений (рисунок 19) и выберем из них наиболее подходящее.

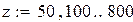
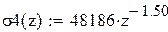
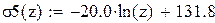
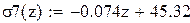
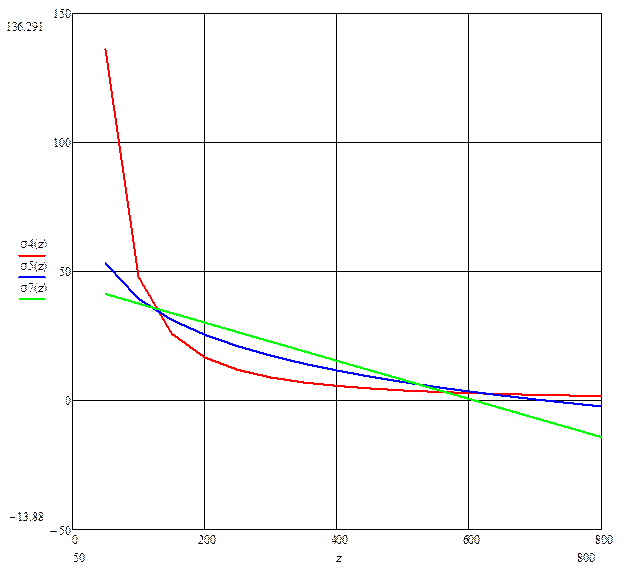
Рисунок 19 – График приближенной зависимости предела прочности от температуры для разных зависимостей

Поскольку значение логарифмической зависимости наиболее близко к экспериментальным данным, будем использовать данное уравнение для построения графика (рисунок 20), не смотря на более низкий коэффициент корреляции. Обозначим температуру символом z, а предел прочности σ8. Также найдем значение предела прочности при температуре 800 °С.

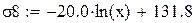
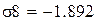
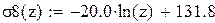
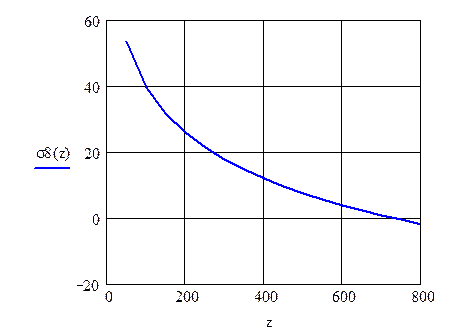
Рисунок 20 – График приближенной зависимости предела прочности от температуры