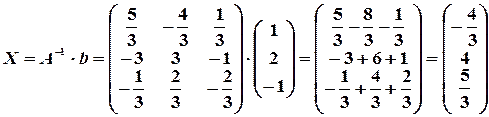Системы линейных уравнений

Система линейных уравнений имеет вид:

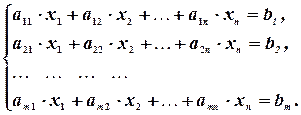
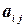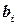
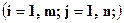Здесь и ‑ заданные, а 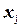‑ неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему в виде:

AX =B

где 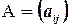- матрица, состоящая из коэффициентов при неизвестных, которая называется матрицей системы, 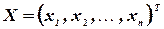, 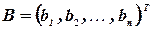- векторы-столбцы, составленные соответственно из неизвестных x_j и из свободных членов b_i.

Упорядоченная совокупность 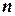вещественных чисел 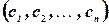называется решением системы, если в результате подстановки этих чисел вместо соответствующих переменных 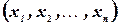каждое уравнение системы обратится в арифметическое тождество.

Система называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.

Матрица

,

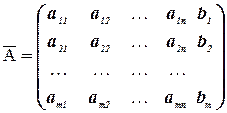образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.

Вопрос о совместности системы решается следующей теоремой.

Теорема Кронекера-Капелли.

Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A и 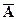совпадают, т.е. .

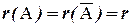Система имеет единственное решение только в том случае, когда
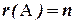. При этом число уравнений - не меньше числа неизвестных 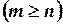; если 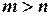, то 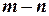уравнений являются следствиями остальных. Если 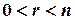, то система является неопределенной.

Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:

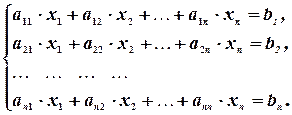
Эти системы решаются одним из следующих способов:

1) методом Гаусса, или методом исключения неизвестных;

2) по формулам Крамера;

3) матричным методом.

Пример 17. Исследовать систему уравнений и решить ее, если она совместна:

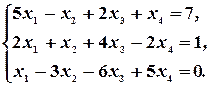
Решение. Выписываем расширенную матрицу системы:

.

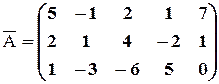Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу 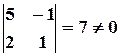; содержащие его миноры третьего порядка равны нулю:

, .

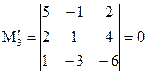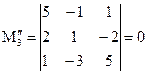Следовательно, ранг основной матрицы системы равен 2, т.е. 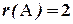. Для вычисления ранга расширенной матрицы 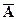рассмотрим окаймляющий минор

,

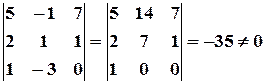значит, ранг расширенной матрицы 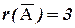. Поскольку 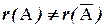, то система несовместна.

А. Метод Гаусса

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных, данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Пример 18. Решить систему уравнений методом Гаусса:

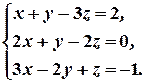
Решение. Выпишем расширенную матрицу данной системы

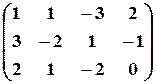
и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

;

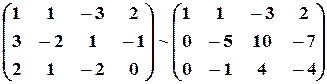б) третью строку умножим на (-5) и прибавим к ней вторую:

.

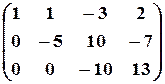В результате всех этих преобразований данная система приводится к треугольному виду:

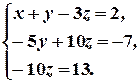
Из последнего уравнения находим 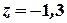. Подставляя это значение во второе уравнение, имеем 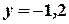. Далее из первого уравнения получим .

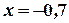Б. Формулы Крамера

Назовем столбцы матрицы следующим образом: первый столбец - 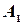, второй столбец - 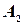, и т.д., последний столбец - 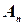. Тогда матрицу 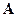можно записать в виде .

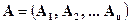Составим 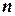дополнительных матриц:

, , …, ,

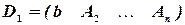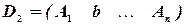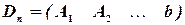и вычислим их определители и определитель исходной матрицы:

, , , …, .

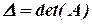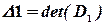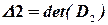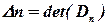Тогда значения неизвестных вычисляются по формулам Крамера:

, , …, .

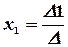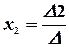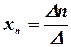Правило Крамера дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по вышеприведенным формулам.

Если главный определитель системы 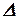и все вспомогательные определители 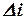равны нулю, то система имеет бесчисленное множество решений.

Если главный определитель системы 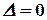, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

Пример 19. Решить систему уравнений методом Крамера.

, .

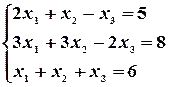
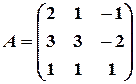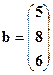Тогда

, , .

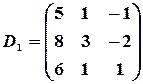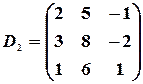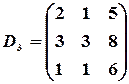Вычисляя определители этих матриц, получаем , , , .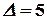

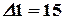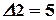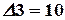И по формулам Крамера находим: , , .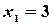

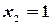В. Матричный метод

Теперь, рассмотрим матричное уравнение 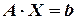. Если у матрицы существует обратная матрица 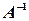, то, умножая матричное уравнение на 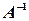слева, получим:

.

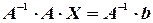По определению обратимости матрицы 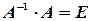и по свойству единичной 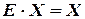, получаем:

.

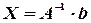Пример 20. Решить систему уравнений с помощью обратной матрицы.

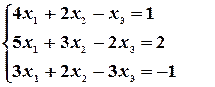
Имеем:

, .

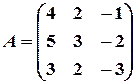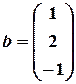Вычислим определитель матрицы 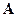, разлагая по первой строке:

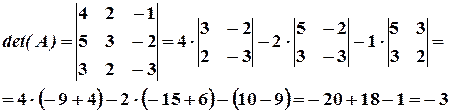
Значит, обратная матрица существует. Вычислим алгебраические дополнения элементов матрицы:

, ,

, ,

, ,

, ,

.

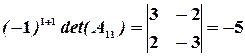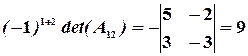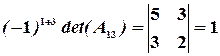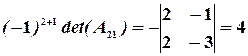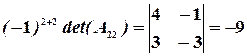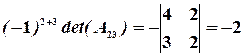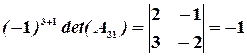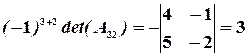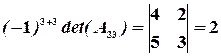Тогда решение системы получается умножением обратной матрицы на столбец свободных членов