Скалярное произведение векторов

Определение и свойства

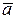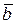Пусть даны два вектора и .Тогда их скалярное произведение определяется из равенства 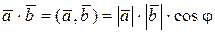, где j - угол между этими векторами.

Если векторы заданы в координатной форме 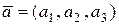, , 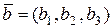то их скалярное произведение вычисляется по формуле:

.

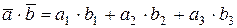Скалярное произведение векторов обладает следующими свойствами:

а) ;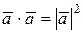

б) если 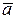^ 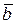(ортогональные вектора), то 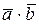= 0;

в) ;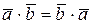

г) ;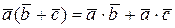

д) 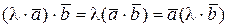, где λ- любое число.

Примеры.

а) Найти скалярное произведение векторов 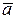= (2, 1, 1) и 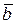= (2, -5, 1).

Из определения имеем = .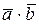

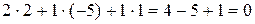б) Даны вектор 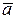= (m, 3, 4) и вектор 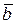= (4, m, -7). При каких значениях m вектор 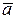ортогонален вектору ?

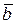Из условий ортогональности имеем: 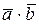= 4m + 3m -28 = 0,

7m = 28, m = 4.

в) Найти 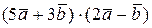, есл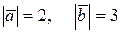и и ^ .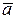

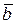Из свойств скалярного произведения имеем: ,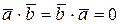

т.к. 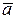^ 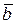, тогда

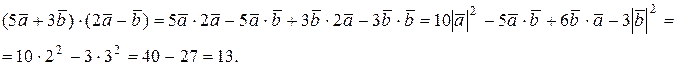
г) Определить угол между векторами 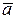= (1, 2, 3) и 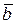= (0, 4, -2).

Так как 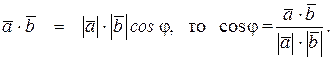Из координатного представления векторов находим 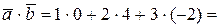0+8-6=2,

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ

Определение векторного произведения

Если вектора 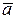и 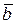заданы в координатной форме 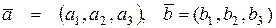то их векторное произведение определяется по формуле:

,

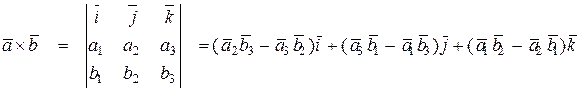где 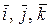-орты осей координат Ox, Oy, Oz, соответственно:

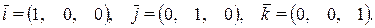
Пример. Найдем векторное произведение векторов .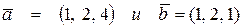

Из приведенной формулы имеем

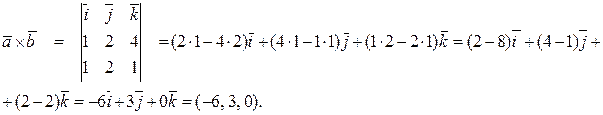
Свойства векторного произведения

Отметим следующие свойства векторного произведения:

а) ;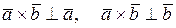

б) 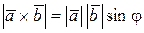, т.е. модуль векторного произведения равен площади параллелограмма, построенного на векторах 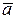и 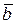как на сторонах;

в) ;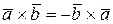

г) 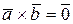, если либо 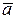= 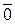, либо 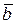= 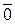, либо вектора 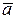и 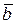коллинеарны;

д) 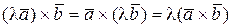, где λ –любое число;

е) .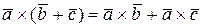

Приведенные свойства позволяют решать многие задачи геометрии и векторного анализа.

Примеры.

а) Вычислим площадь параллелограмма, построенного на векторах

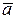= (3, 6, -2) и 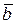= (-2, 3, 6).

Имеем

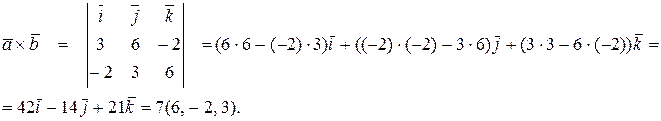Тогда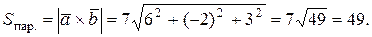

б) Вычислим площадь треугольника с вершинами А(1, 1, 1), В(2, 3, 4), С(4, 3, 2).

На сторонах АВ и АС достроим треугольник до параллелограмма АВСD. Тогда 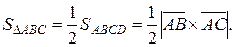Так как 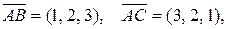то

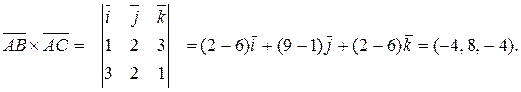
Следовательно, 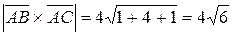, а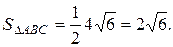

в) Вычислим площадь параллелограмма, построенного на векторах

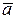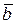+ 3 и 3 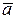+ 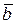, если 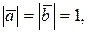а угол между векторам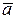и и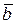

равен p/6.

Заметим, что 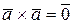для любого вектора. Следовательно,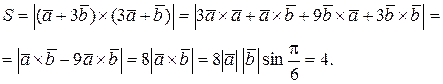

Итак, искомая площадь параллелограмма S=4.

г) Известно, что вектор 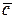ортогонален векторам 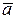= (3, 2, 1) и

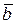= (2, 3, 1), а | 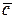| = 3. Найти вектор .

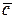Так как вектор 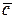ортогонален векторам 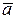и, 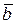то он коллинеарен вектору 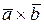. Имеем

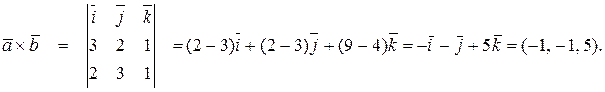
Таким образом, 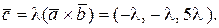Следовательно, 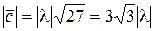, 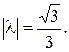Итак, имеем два вектора, удовлетворяющих условиям задачи: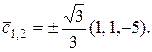

же удовлетворяет условию 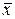(1, -7, 2)=10.

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Определение и свойства

Смешанным произведением трех векторов

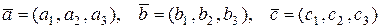называется число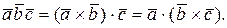

Смешанное произведение обладает следующими свойствами:

а) 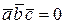, если все три вектора параллельны одной и той же плоскости (компланарны);

б)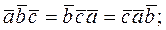

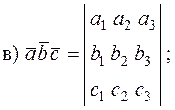
г) объем параллелепипеда, построенного на векторах 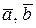и 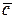, равен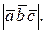

Примеры.

а) Найти смешанное произведение векторов 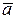=(5, 7, 2), 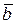= (1, -1, 1),

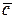= (2, 2, 1).

Из определения имеем

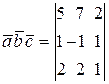= -5 + 14 + 4 + 4 - 10 - 7 = 0, т.е. вектора 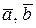и 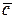компланарны.

б) Найти объем треугольной пирамиды с вершинами А(2, 2, 2),

В(4, 3, 3), С(4, 5, 4), D(5, 5, 6).

Из свойств смешанного произведения заключаем, что искомый объем равен

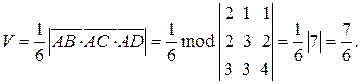
в) Вычислим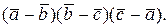

Используя определение смешанного произведения и свойства векторного и скалярного произведений получаем

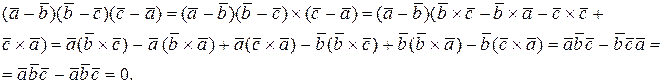
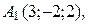
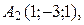
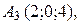
г) По координатам вершин пирамиды 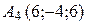найти: 1) длины ребер 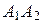и 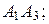2) угол между ребрам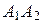и и 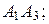3) площадь грани 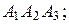4) объем пирамиды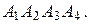

Находим векторы 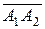и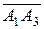

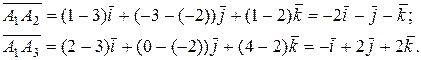
Длины векторов, т.е. длины ребер 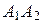и 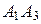, таковы:

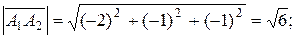
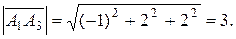
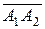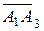Скалярное произведение векторов и равно

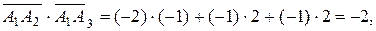
а косинус угла между ними:

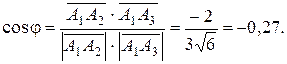
Отсюда следует, что 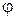- тупой угол, равный 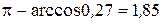(рад.) с точностью до 0,01. Это и есть искомый угол между ребрам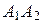и и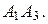

Площадь грани 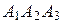равна половине площади параллелограмма, построенного на векторах 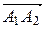и 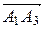, т.е. половине модуля векторного произведения этих векторов:

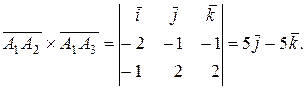
Следовательно,

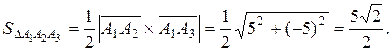
Объем 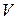пирамиды равен 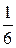объема параллелепипеда, построенного на векторах 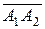, , 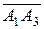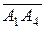. Вектор 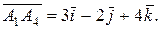Итак,

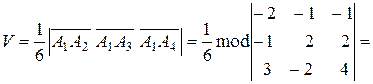
ПРЯМАЯ НА ПЛОСКОСТИ