Завдання до контрольної роботи 150
Л. І. Кублій, М. В. Ногін
Вибрані розділи
дискретної математики
Алгебричні структури
Алгебра логіки
Математична логіка
Київ
НТУУ “КПІ”
УДК
ББК
Гриф надано Методичною радою НТУУ “КПІ”
(Протокол № від 2011 р.)
Рецензенти: Летічевський Олександр Адольфович, академік НАН України,
доктор фізико-математичних наук, професор,
Інститут кібернетики ім. В.М.Глушкова НАН України
Гладкий Анатолій Васильович, доктор фізико-математичних наук,
професор, Інститут кібернетики ім. В.М.Глушкова НАН України
Дичка Іван Андрійович, доктор технічних наук, професор Національний технічний університет України “Київський політехнічний інститут”
Відповідальний
редактор С.О. Лук’яненко, доктор технічних наук, професор,
Національний технічний університет України
“Київський політехнічний інститут”
 |
ЗМІСТ
Перелік умовних скорочень 5
ВСТУП 7
АЛГЕБРИЧНІ СТРУКТУРИ 8
Частина 1. ОСНОВНІ АЛГЕБРИЧНІ СТРУКТУРИ 8
1.1. Поняття алгебри 8
1.2. Унарні й бінарні операції 9
1.3. Поняття алгебричної структури 13
1.4. Властивості бінарних операцій 13
1.5. Алгебричні структури з однією бінарною операцією 14
1.6. Алгебричні структури з двома бінарними операціями 16
1.7. Додаткові приклади, інтерпретації, властивості 18
1.8. Поняття векторного простору 20
Питання для самоконтролю 21
АЛГЕБРА ЛОГІКИ 23
Частина 2. ФУНКЦІЇ АЛГЕБРИ ЛОГІКИ 23
2.1. Алгебра Буля і алгебра логіки 23
2.2. Логічні функції однієї і двох змінних 27
2.3. Властивості елементарних логічних функцій 29
2.4. Формули в алгебрі логіки 30
2.5. Диз’юнктивні й кон’юктивні нормальні форми алгебри Буля 31
2.6. Двоїсті функції 32
2.7. Досконалі диз’юнктивні й кон’юнктивні нормальні форми 36
Питання для самоконтролю 42
Частина 3. АЛГЕБРА ЖЕГАЛКІНА 44
3.1. Поняття алгебри Жегалкіна 44
3.2. Властивості операцій алгебри Жегалкіна 45
3.3. Многочлени Жегалкіна 46
Питання для самоконтролю 51
Частина 4. ПОВНОТА І ЗАМКНУТІСТЬ СИСТЕМИ
ЛОГІЧНИХ ФУНКЦІЙ 53
4.1. Поняття повної системи функцій 53
4.2. Замикання множини логічних функцій 54
4.3. Основні замкнуті класи логічних функцій 55
4.4. Критерій Поста повноти системи функцій 57
Питання для самоконтролю 59
Частина 5. МІНІМІЗАЦІЯ ЛОГІЧНИХ ФУНКЦІЙ 60
5.1. Поняття мінімізації 60
5.2. Побудова скорочених ДНФ 62
5. 3. Побудова тупикових ДНФ. Метод імплікантних
таблиць Квайна. Метод Петрика 66
5.4. Мінімізація на основі карт Карно 70
Питання для самоконтролю 74
МАТЕМАТИЧНА ЛОГІКА 75
Частина 6. ЛОГІКА ВИСЛОВЛЮВАНЬ 75
6.1. Загальна характеристика логіки висловлювань 75
6.2. Висловлювання. Формули 76
6.3. Система обчислень 80
6.4. Еквівалентні перетворення формул 82
6.5. Система формального виведення 86
6.6. Система природного виведення 93
6.7. Аксіоматичні системи числення висловлювань 110
Питання для самоконтролю 122
Частина 7. ЛОГІКА ПРЕДИКАТІВ 125
7.1. Найпростіші визначення й поняття 125
7.2. Операції з предикатами 129
7.3. Формули логіки предикатів. Еквівалентні
перетворення формул 134
7.4. Пряма, обернена, протилежна теореми. Необхідна
й достатня умови 139
7.5. Випереджальні нормальні форми 141
7.6. Аксіоми числення предикатів. Формальне виведення 144
Питання для самоконтролю 148
ЗАВДАННЯ ДО КОНТРОЛЬНОЇ РОБОТИ 150
Розділ “Алгебричні структури” 150
Розділ “Алгебра логіки” 154
Розділ “Математична логіка” 158
Список використаної літератури 164
Предметний покажчик 165
ПЕРЕЛІК УМОВНИХ СКОРОЧЕНЬ
 — квантор “для всіх”;
— квантор “для всіх”;
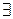 — квантор існування;
— квантор існування;
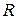 — множина дійсних чисел;
— множина дійсних чисел;
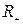 — множина додатних дійсних чисел;
— множина додатних дійсних чисел;
N — множина натуральних чисел;
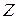 — множина цілих чисел;
— множина цілих чисел;
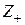 або
або  — множина цілих невід’ємних чисел;
— множина цілих невід’ємних чисел;
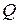 — множина раціональних чисел;
— множина раціональних чисел;
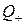 — множина додатних раціональних чисел;
— множина додатних раціональних чисел;
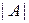 — потужність множини А;
— потужність множини А;
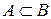 — строге включення;
— строге включення;
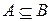 — нестроге включення;
— нестроге включення;
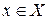 — елемент x належить множині X;
— елемент x належить множині X;
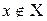 — елемент x не належить множині X;
— елемент x не належить множині X;
 — універсальна множина;
— універсальна множина;
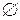 — порожня множина;
— порожня множина;
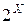 — множина всіх підмножин множини X;
— множина всіх підмножин множини X;
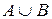 — об’єднання множин А і В;
— об’єднання множин А і В;
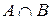 — перетин множин А і В;
— перетин множин А і В;
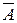 — доповнення множини А до універсальної;
— доповнення множини А до універсальної;
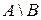 — різниця множин А і В;
— різниця множин А і В;
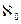 — потужність злічуваної множини (алеф нуль)
— потужність злічуваної множини (алеф нуль)
 — потужність множини континуум;
— потужність множини континуум;
 — декартів добуток множин А і В;
— декартів добуток множин А і В;
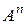 — декартів степінь множини А;
— декартів степінь множини А;
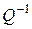 — обернене відношення до відношення Q;
— обернене відношення до відношення Q;
 — композиція відношень Q і S;
— композиція відношень Q і S;
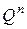 — степінь відношення Q;
— степінь відношення Q;
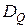 — область визначення відношення Q;
— область визначення відношення Q;
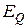 — область значень відношення Q;
— область значень відношення Q;
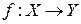 — відображення;
— відображення;

 — відношення еквівалентності;
— відношення еквівалентності;
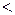 — відношення строгого порядку;
— відношення строгого порядку;
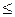 — відношення нестрогого порядку;
— відношення нестрогого порядку;
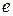 — одиничний елемент;
— одиничний елемент;
0 — одиничний елемент відносно додавання;
1 — одиничний елемент відносно множення;
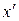 — обернений елемент до елемента x;
— обернений елемент до елемента x;
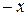 — обернений елемент до елемента х відносно додавання;
— обернений елемент до елемента х відносно додавання;
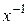 — обернений елемент до елемента х відносно множення;
— обернений елемент до елемента х відносно множення;
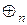 — додавання за модулем n;
— додавання за модулем n;
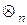 — множення за модулем n;
— множення за модулем n;
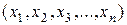 — інтерпретація логічної функції, двійкове слово, булів кортеж;
— інтерпретація логічної функції, двійкове слово, булів кортеж;
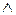 — кон’юнкція;
— кон’юнкція;
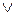 — диз’юнкція;
— диз’юнкція;
 — заперечення;
— заперечення;
 або
або  — еквівалентність;
— еквівалентність;
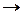 — імплікація;
— імплікація;
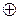 — сума за модулем 2;
— сума за модулем 2;
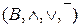 — алгебрична структура — булева алгебра;
— алгебрична структура — булева алгебра;
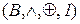 — алгебрична структура — алгебра Жегалкіна;
— алгебрична структура — алгебра Жегалкіна;
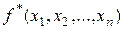 — функція, двоїста до функції
— функція, двоїста до функції 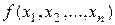 ;
;
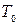 — клас функцій, які зберігають нуль;
— клас функцій, які зберігають нуль;
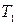 — клас функцій, які зберігають одиницю;
— клас функцій, які зберігають одиницю;
 — клас самодвоїстих функцій;
— клас самодвоїстих функцій;
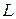 — клас лінійних функцій;
— клас лінійних функцій;
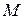 — клас монотонних функцій.
— клас монотонних функцій.
ВСТУП
У навчальному посібнику в доступній формі викладено три важливі розділи курсу дискретної математики — алгебричні структури, алгебру логіки й математичну логіку.
При вивченні алгебричних структур розглядаються властивості операцій, наводиться класифікація простих алгебричних структур, якими є півгрупи, моноїди, групи, кільця, поля.
При вивченні алгебри логіки значна увага приділяється алгебрі Буля й алгебрі Жегалкіна. Ці алгебри є типовими прикладами загальної теорії про алгебричні структури. В алгебрі логіки також розглядається питання повноти системи логічних функцій і можливі підходи до розв’язання задачі мінімізації логічних функцій.
У частинах, присвячених математичній логіці, розглядаються логіка висловлювань (на прикладах кількох класичних її різновидів) і теорія предикатів першого порядку.
Потрібна для опанування матеріалу посібника математична підготовка обмежується поняттями розділу “Елементи теорії множин і відношення” і, звичайно ж, знаннями з елементарної математики за середню школу.
Усі ключові теоретичні поняття забезпечено достатньою кількістю задач і вправ, наведено завдання до модульної контрольної роботи.
Частини 1 – 4 написано М. В. Ногіним, частини 5 і 6 — Л. І. Кублій, частину 7 — авторами сумісно.
Посібник розрахований на студентів, які спеціалізуються в галузі прикладної математики, математичного забезпечення комп’ютерних систем, спеціального зв’язку тощо.
АлгебрИчні структури
Одним із основних завдань теорії універсальних алгебр є вивчення властивостей і взаємозв’язку аксіоматизованих класів алгебр — алгебричних структур, таких, як групи, кільця, поля тощо. Ці структури дають можливість описувати дискретну будову й дискретність функціонування кібернетичних й інтелектуальних систем.
Частина 1. ОСНОВНІ АлгебрИчні структури
1.1. Поняття алгебри
Визначення 1.1. Алгеброю(ще кажуть: універсальною алгеброю) називають непорожню множину елементів разом з операціями, визначеними і замкненими на цій множині.
Дану непорожню множину називають носієм(або основною множиною) алгебри. Якщо носієм алгебри є множина А, а її операціями є операції 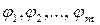 , то алгебру позначають так:
, то алгебру позначають так: 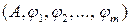 .
.
Операція є замкненою (або ще кажуть: внутрішньою) на заданій множині, якщо результат її застосування до будь-яких елементів цієї множини належить цій са́мій множині.
Алгебри можна визначати на множинах N натуральних чисел, Z цілих чисел, на множині R дійсних чисел (яка не є дискретною), множині комплексних чисел К, а також на довільних множинах і відношеннях.
Приклад 1.1. Множина 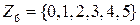 з операцією звичайного додавання (+) не є алгеброю, оскільки операція додавання не замкнена на цій множині: наприклад,
з операцією звичайного додавання (+) не є алгеброю, оскільки операція додавання не замкнена на цій множині: наприклад, 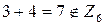 . Але множина
. Але множина 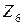 з операцією додавання за модулем 5 (
з операцією додавання за модулем 5 ( 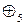 ; при цьому операція додавання за модулем m визначається так:
; при цьому операція додавання за модулем m визначається так: 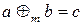 , де
, де 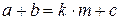 ,
, 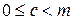 ,
, 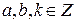 ,
, 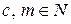 ) утворює алгебру
) утворює алгебру 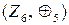 , оскільки дана операція замкнена на множині
, оскільки дана операція замкнена на множині 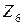 : наприклад,
: наприклад, 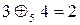 ,
, 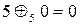 ,
,  .
.
1.2. Унарні й бінарні операції
Визначення 1.2. Операцієюна множині L називають функцію f, тобто відображення виду 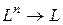 , де
, де 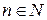 . Така операція однозначна. Вона також замкнута, тобто її область визначення
. Така операція однозначна. Вона також замкнута, тобто її область визначення 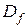 і область значень
і область значень 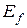 належать множині L.
належать множині L.
Операцію виду 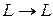 називають унарною, а операцію виду
називають унарною, а операцію виду 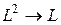 — бінарною. Символи операцій називають операторами.
— бінарною. Символи операцій називають операторами.
Приклад 1.2. Прикладами унарних операцій є:
а) зміна знака на множинах Z і R: −5; −3,1415; −18,3; 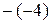 ;
; 
б) операція піднесення до степеня на множинах N, Z і R: 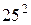 ; (–1)2; (7,8)3;
; (–1)2; (7,8)3; 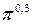 ;
;
в) доповнення в алгебрі множин: 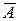 .
.
Прикладами бінарних операцій є:
а) на множині R — арифметичні дії додавання (+), віднімання (–), множення ( 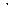 ), ділення (
), ділення ( 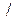 );
);
б) в алгебрі множин — об’єднання ( 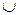 ), перетин (
), перетин ( 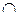 ), різниця (
), різниця ( 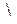 ), пряма сума (
), пряма сума ( 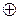 ), яку ще називають симетричною різницею, декартів добуток (
), яку ще називають симетричною різницею, декартів добуток ( 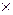 ).
).
Бінарні операції можна записати одним із трьох способів: інфіксним (infix, яким ми звикли користуватися) — оператор ставиться між операндами; префіксним (prefix, який ще називають прямим польським записом[1]) — оператор ставиться перед операндами; постфіксним (postfix, який ще називають зворотним польським записом) — оператор ставиться після операндів.
Приклад 1.3. а) Розглянемо варіанти запису бінарної операції додавання: 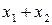 — infix;
— infix; 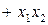 — prefix;
— prefix; 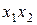 + — postfix.
+ — postfix.
б) Розглянемо варіанти запису алгебричного виразу: 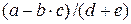 — infix;
— infix; 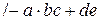 — prefix;
— prefix; 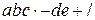 — postfix.
— postfix.
Надалі ми користуватимемося виключно інфіксним записом, проте зазначимо, що при комп’ютерній обробці інформації в алгоритмах обчислень другий і третій варіанти зручніші, оскільки в них не використовуються дужки для встановлення порядку обчислень.
Крім вказаних, добре відомих операцій — арифметичних дій і операцій над множинами, існує багато інших операцій.
Так, в алгебрі висловлювань, яка є найпростішою з формальних логічних теорій і в якій задано логічні операції над висловлюваннями[2], складні висловлювання одержують з простих за допомогою унарних і бінарних операцій (їх називають зв’я́зками): заперечення ( 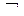 ), кон’юнкції (
), кон’юнкції ( 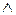 ), диз’юнкції (
), диз’юнкції ( 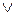 ), імплікації (→), еквівалентності (
), імплікації (→), еквівалентності ( 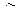 ) та ін. Розглянемо ці операції докладніше.
) та ін. Розглянемо ці операції докладніше.
Запереченнямвисловлювання 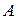 називають висловлювання
називають висловлювання 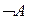 , якщо воно істинне (І), коли
, якщо воно істинне (І), коли 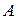 — хибне (Х), і хибне, коли
— хибне (Х), і хибне, коли 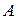 — істинне. Таблиця істинності для заперечення проста:
— істинне. Таблиця істинності для заперечення проста:
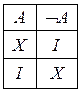
Кон’юнкцієюдвох висловлювань А і В називають висловлювання виду 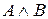 , яке істинне тоді і тільки тоді, коли
, яке істинне тоді і тільки тоді, коли 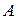 і
і 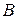 одночасно істинні. Таблиця істинності для кон’юнкції має такий вигляд:
одночасно істинні. Таблиця істинності для кон’юнкції має такий вигляд:
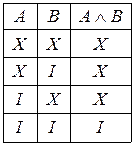
Диз’юнкцієюдвох висловлювань А і В, називають висловлювання виду 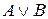 , яке істинне, якщо хоча б одне із даних висловлювань істинне. Таблиця істинності для диз’юнкції має такий вигляд:
, яке істинне, якщо хоча б одне із даних висловлювань істинне. Таблиця істинності для диз’юнкції має такий вигляд:

Імплікацієюдвох висловлювань А і В називають висловлювання виду 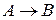 , якщо воно хибне тоді і тільки тоді, коли А істинне, а В хибне. Таблиця істинності для імплікації має такий вигляд:
, якщо воно хибне тоді і тільки тоді, коли А істинне, а В хибне. Таблиця істинності для імплікації має такий вигляд:
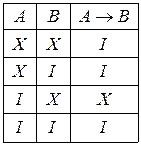
Еквівалентністюдвох висловлювань А і В називають висловлювання 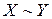 , якщо воно істинне тоді і тільки тоді, коли А і В обоє істинні або обоє хибні. Таблиця істинності для еквівалентності має такий вигляд:
, якщо воно істинне тоді і тільки тоді, коли А і В обоє істинні або обоє хибні. Таблиця істинності для еквівалентності має такий вигляд:
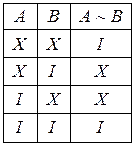
Розглянемо також деякі інші зв’я́зки.
Штрих Шеффера(або антикон’юнкція): 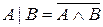 . Таблиця істинності для штриха Шеффера має такий вигляд:
. Таблиця істинності для штриха Шеффера має такий вигляд:
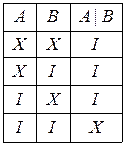
Стрілка Пірса(або антидиз’юнкція): 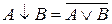 . Таблиця істинності для стрілки Пірса має такий вигляд:
. Таблиця істинності для стрілки Пірса має такий вигляд:
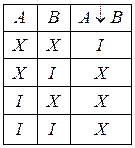
Сума за модулем два(або антиеквівалентність):  . Таблиця істинності для суми за модулем два має такий вигляд:
. Таблиця істинності для суми за модулем два має такий вигляд:
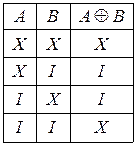
На основі простого логічного аналізу, зокрема аналізу таблиць істинності, зазначимо, що імплікація двох висловлювань принципово відмінна від диз’юнкції, кон’юнкції й еквівалентності, оскільки вона несиметрична. Справді, для вказаних операцій не має значення порядок операндів (тобто, вони комутативні):
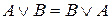 ,
, 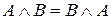 ,
, 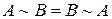 ,
,
але 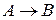 не еквівалентне
не еквівалентне 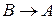 .
.
Розглянемо всі імплікації, які можна утворити з двох висловлювань А і В. У таблиці істинності подано чотири імплікації:
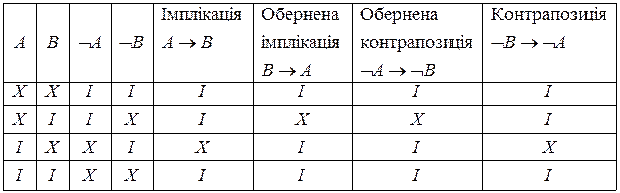
Звідси видно, що 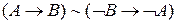 , також
, також  .
.
Надалі для позначення абстрактних бінарних операцій будемо використовувати символи 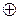 і
і 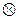 .
.
1.3. Поняття алгебричної структури
Визначення 1.3. Алгебричною структуроюназивають алгебру, операціями якої є одна чи дві бінарні операції і довільна кількість унарних операцій (хоча унарних операцій може й не бути).
Операції алгебричної структури мають задовольняти певні аксіоми (властивості). Залежно від кількості операцій і виконання певної сукупності аксіом розрізняють різні алгебричні структури. Ми ознайомимося з такими алгебричними структурами, як півгрупи, моноїди, групи, кільця, поля. Ця класифікація є основною не тільки для вивчення лінійної алгебри, теорії матриць, обробки числових масивів, але є також базою вивчення алгебри логіки, зокрема алгебри Буля й алгебри Жегалкіна.
1.4. Властивості бінарних операцій
Нехай на множині A визначено дві бінарні операції 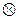 і
і 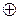 .
.
Операції 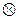 і
і 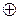 комутативні, якщо a
комутативні, якщо a 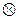 b=b
b=b 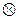 a, a
a, a 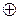 b=b
b=b 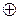 a .
a .
Операції 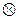 і
і 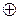 асоціативні, якщо
асоціативні, якщо 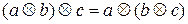 ,
, 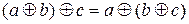 .
.
Якщо для будь-яких 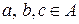 виконується рівність
виконується рівність 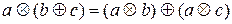 , то бінарна операція
, то бінарна операція 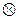 дистрибутивна відносно операції
дистрибутивна відносно операції 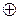 .
.
Приклад 1.4. а) На множині дійсних чисел R звичайне додавання (+) є комутативною й асоціативною операцією, а операція віднімання (–) — не комутативна й не асоціативна: 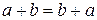 , але
, але 
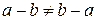 ;
; 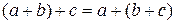 , але
, але 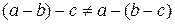 . Також на множині R бінарна операція множення (
. Також на множині R бінарна операція множення ( 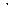 ) дистрибутивна відносно додавання (+), проте додавання не дистрибутивне відносно множення:
) дистрибутивна відносно додавання (+), проте додавання не дистрибутивне відносно множення: 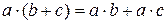 , але
, але 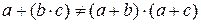 .
.
б) В алгебрі множин операції об’єднання ( 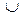 ) й перетину (
) й перетину ( 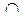 ) комутативні:
) комутативні: 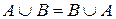 ,
, 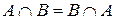 , асоціативні:
, асоціативні: 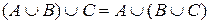 ,
, 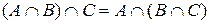 і дистрибутивні одна відносно одної:
і дистрибутивні одна відносно одної: 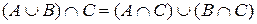 ,
, 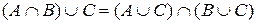 .
.
Одиницею(або одиничним елементом) для бінарної операції 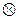 (чи для операції
(чи для операції 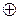 )на множині A називають такий елемент
)на множині A називають такий елемент 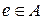 , що для будь-якого
, що для будь-якого 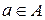 виконується рівність:
виконується рівність:
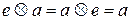 (чи
(чи 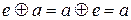 ),
),
якщо такий елемент e існує.
Приклад 1.5. а) Якщо на множині дійсних чисел R бінарна операція є множенням ( 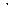 ), то
), то  , а для звичайного додавання (+)
, а для звичайного додавання (+) 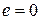 .
.
б) В алгебрі множин для бінарної операції об’єднання ( 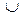 )
) 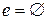 , а для операції перетину (
, а для операції перетину ( 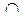 ) —
) — 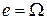 .
.
Нехай операція 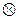 на множині
на множині 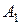 з одиницею
з одиницею 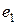 і два елементи
і два елементи 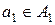 ,
, 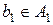 задовольняють рівності a1
задовольняють рівності a1 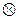 b1=b1
b1=b1 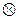 a1=e1. Також нехай операція
a1=e1. Також нехай операція 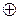 на множині
на множині 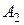 з одиницею
з одиницею  і два елементи
і два елементи 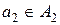 ,
, 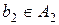 задовольняють рівності
задовольняють рівності 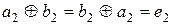 . Тоді
. Тоді 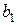 називають оберненим елементомдо
називають оберненим елементомдо 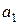 відносно операції
відносно операції 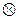 (а
(а 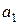 — оберненим елементом до
— оберненим елементом до 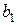 ). Відповідно,
). Відповідно, 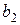 називають оберненим елементом до
називають оберненим елементом до 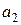 відносно операції
відносно операції 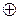 (а
(а 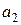 — оберненим елементом до
— оберненим елементом до 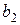 ).
).
Приклад 1.6. Якщо на множині дійсних чисел R бінарна операція є звичайним додаванням (+), то для будь-якого елемента 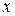 оберненим буде елемент (
оберненим буде елемент ( 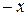 ), а якщо бінарна операція є операцією множення (
), а якщо бінарна операція є операцією множення ( 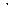 ), то для елемента
), то для елемента 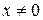 оберненим буде елемент
оберненим буде елемент 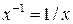 .
.
Нижче розглянемо класифікацію простих алгебричних структур.
1.5. Алгебричні структури з однією бінарною операцією
Найважливішими простими алгебричними структурами, які мають тільки одну бінарну операцію, є півгрупи, моноїди й групи.
Визначення 1.4. Півгрупою 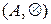 називають алгебричну структуру з множиною-носієм A і однією бінарною операцією
називають алгебричну структуру з множиною-носієм A і однією бінарною операцією 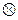 , яка задовольняє тільки одну властивість — властивість асоціативності. Тобто для будь-яких
, яка задовольняє тільки одну властивість — властивість асоціативності. Тобто для будь-яких 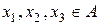 виконується:
виконується:
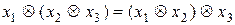 .
.
Приклад 1.7. Алгебрична структура  — множина натуральних чисел з бінарною операцією звичайного додавання (+) є півгрупою.
— множина натуральних чисел з бінарною операцією звичайного додавання (+) є півгрупою.
Визначення 1.5. Моноїдомназивають півгрупу з одиницею. Моноїд має такі дві властивості:
1) асоціативність — для будь-яких 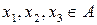 виконується рівність
виконується рівність 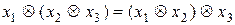 ;
;
2) існує одиничний елемент 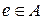 такий, що для будь-якого
такий, що для будь-якого 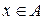 виконується рівність
виконується рівність  .
.
Одиничний елемент в моноїді — єдиний. Справді, якщо 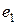 — інша одиниця моноїда, тоді:
— інша одиниця моноїда, тоді:
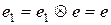 .
.
Приклад 1.8. Структури 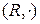 ,
, 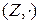 ,
, 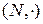 — множини дійсних, цілих, натуральних чисел з бінарною операцією звичайного множення (
— множини дійсних, цілих, натуральних чисел з бінарною операцією звичайного множення ( 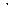 ) є моноїдами. При цьому одиничний елемент e=1.
) є моноїдами. При цьому одиничний елемент e=1.
Визначення 1.6. Групою 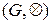 називають алгебричну структуру з множиною-носієм G і однією бінарною операцією
називають алгебричну структуру з множиною-носієм G і однією бінарною операцією 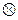 , замкнутою в G, яка має такі три властивості:
, замкнутою в G, яка має такі три властивості:
1) асоціативність — для будь-яких 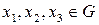 виконується рівність
виконується рівність 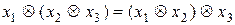 ;
;
2) для будь-якого 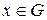 існує одиничний елемент
існує одиничний елемент 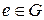 такий, що
такий, що  ;
;
3) для будь-якого 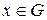 існує обернений елемент
існує обернений елемент 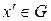 такий, що
такий, що 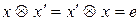 .
.
Отже, група — це моноїд, у якому для кожного елемента існує обернений елемент.
Для довільного елемента х групи G існує лише один обернений елемент 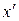 . Справді, якщо їх є два —
. Справді, якщо їх є два — 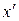 і
і 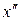 , тоді, враховуючи означення одиничного і оберненого елементів, а також властивість асоціативності, матимемо:
, тоді, враховуючи означення одиничного і оберненого елементів, а також властивість асоціативності, матимемо:

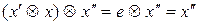 .
.
Отже, 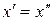 , тобто обернений елемент єдиний.
, тобто обернений елемент єдиний.
На множині дійсних чисел R, залежно від групової операції — додавання (+) чи множення ( 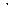 ), групу називають адитивноючи мультиплікативною.
), групу називають адитивноючи мультиплікативною.
Визначення 1.7. Комутативну групу називають абелевою[3].
Таким чином, для того щоб група була абелевою, крім вказаних в означенні групи трьох властивостей, ще має виконуватися властивість комутативності, тобто для будь-яких  має виконуватися рівність
має виконуватися рівність 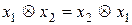 .
.
Приклад 1.9. Абелевою групою є множина дійсних чисел R з бінарною операцією звичайного додавання (+) — 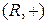 . Для неї одиничний елемент
. Для неї одиничний елемент 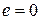 , обернений елемент
, обернений елемент 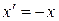 . Проте
. Проте 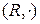 — множина дійсних чисел з операцією звичайного множення (
— множина дійсних чисел з операцією звичайного множення ( 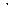 ) є моноїдом, але не групою, оскільки для елемента
) є моноїдом, але не групою, оскільки для елемента 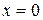 на множині R не існує оберненого елемента; для інших
на множині R не існує оберненого елемента; для інших 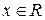 (
( 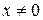 )оберненими елементами є
)оберненими елементами є 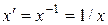 .
.
Приклад 1.10. Нехай  — множина всіх квадратних матрицьпорядку n з дійсними елементами. Алгебрична структура
— множина всіх квадратних матрицьпорядку n з дійсними елементами. Алгебрична структура 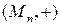 — це комутативний моноїд, у якому одиничним елементом e є нульова матриця. Структура
— це комутативний моноїд, у якому одиничним елементом e є нульова матриця. Структура 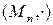 — некомутативний моноїд (бо
— некомутативний моноїд (бо 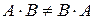 ), у якому e — одинична матриця. Тут про групу не йдеться, оскільки обернена матриця
), у якому e — одинична матриця. Тут про групу не йдеться, оскільки обернена матриця 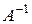 не існує, якщо
не існує, якщо 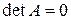 .На множині всіх квадратних матриць e і
.На множині всіх квадратних матриць e і 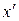 єдині, якщо вони існують.
єдині, якщо вони існують.
1.6. Алгебричні структури з двома бінарними операціями
Розглянемо класифікацію простих алгебричних структур за наявності двох бінарних операцій: множення ( 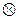 ) і додавання (
) і додавання ( 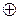 ). Такими алгебричними структурами є кільце і поле.
). Такими алгебричними структурами є кільце і поле.
Визначення 1.8. Кільцем 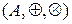 називають алгебричну структуру з множиною-носієм А і визначеними на ній двома бінарними операціями
називають алгебричну структуру з множиною-носієм А і визначеними на ній двома бінарними операціями  і
і 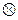 , причому:
, причому:
1) множина А і операція  утворюють абелеву групу, тобто операція
утворюють абелеву групу, тобто операція  асоціативна — для будь-яких
асоціативна — для будь-яких 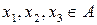 виконується рівність
виконується рівність 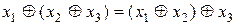 , комутативна — для будь-яких
, комутативна — для будь-яких 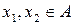 виконується рівність
виконується рівність  , для будь-якого
, для будь-якого 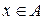 існує одиничний елемент
існує одиничний елемент 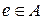 такий, що
такий, що 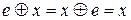 і для будь-якого
і для будь-якого 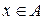 існує обернений елемент
існує обернений елемент 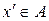 такий, що
такий, що 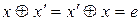 ;
;
2) множина А і операція 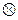 утворюють півгрупу, тобто операція
утворюють півгрупу, тобто операція 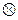 асоціативна — для будь-яких
асоціативна — для будь-яких 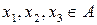 виконується рівність
виконується рівність 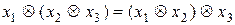 );
);
3) операція  дистрибутивна відносно операції
дистрибутивна відносно операції  зліва і справа, тобто для будь-яких
зліва і справа, тобто для будь-яких 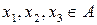 виконуються рівності:
виконуються рівності:
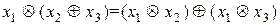 ,
,
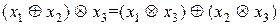 .
.
Кільце комутативне, якщо на множині А операція 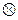 комутативна, тобто : для будь-яких
комутативна, тобто : для будь-яких 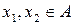 виконується рівність
виконується рівність 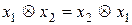 .
.
Кільце називають кільцем з одиницею, якщо існує одиничний елемент e відносно множення 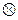 (тобто для будь-якого
(тобто для будь-якого 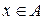 існує одиничний елемент
існує одиничний елемент 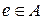 такий, що
такий, що  ).
).
Визначення 1.9. Полемназивають комутативне кільце з одиницею, в якому для кожного ненульового елемента існує обернений елемент відносно операції 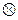 .
.
Отже, поле — це множина елементів А, на якій визначено бінарні операції 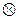 і
і 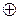 з властивостями комутативності й асоціативності, а також властивістю дистрибутивності операції
з властивостями комутативності й асоціативності, а також властивістю дистрибутивності операції 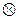 відносно
відносно  , крім того, відносно обох операцій існують нейтральні елементи, і для будь-якого
, крім того, відносно обох операцій існують нейтральні елементи, і для будь-якого 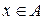 існує обернений елемент відносно операції
існує обернений елемент відносно операції  , і для будь-якого
, і для будь-якого 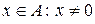 існує обернений елемент відносно операції
існує обернений елемент відносно операції 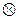 .
.
Приклад 1.11. Множини дійсних, раціональних і комплексних чисел із звичайними операціями додавання (+) і множення ( 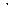 ) утворюють поля
) утворюють поля 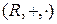 ,
, 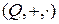 ,
, 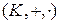 ; при цьому одиничним і оберненим (для кожного ненульового елемента) елементами для множення є
; при цьому одиничним і оберненим (для кожного ненульового елемента) елементами для множення є  ,
, 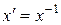 , а для додавання —
, а для додавання — 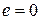 ,
,  . Множина цілих чисел із операціями додавання (+) і множення (
. Множина цілих чисел із операціями додавання (+) і множення ( 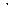 ) є кільцем з одиницею
) є кільцем з одиницею  , але поля не утворює, оскільки для жодного елемента, крім 1 і −1, немає оберненого.
, але поля не утворює, оскільки для жодного елемента, крім 1 і −1, немає оберненого.
1.7. Додаткові приклади, інтерпретації, властивості
Прикладом моноїда є множина всіх перетворень довільної множини А, які мають властивість асоціативності; при цьому роль одиниці виконує тотожне перетворення.
Якщо кількість елементів скінченної множини А є її потужністю 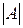 , то кількість елементів скінченної групи G (а також і півгрупи) називають порядком групи(півгрупи). Якщо множина А нескінченна, але злічувана, то її потужність дорівнює
, то кількість елементів скінченної групи G (а також і півгрупи) називають порядком групи(півгрупи). Якщо множина А нескінченна, але злічувана, то її потужність дорівнює 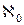 , а якщо незлічувана, то має потужність континуум с; відповідним буде й порядок групи (півгрупи).
, а якщо незлічувана, то має потужність континуум с; відповідним буде й порядок групи (півгрупи).
Розглянемо приклади груп.
1. Множина Z цілих чисел утворює абелеву групу відносно операції звичайного додавання (+). Порядок групи 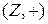 дорівнює потужності множини Z, тобто
дорівнює потужності множини Z, тобто 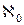 .
.
2. Множина 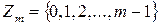 цілих невід’ємних лишків за модулем m утворює групу відносно операції додавання за модулем m (
цілих невід’ємних лишків за модулем m утворює групу відносно операції додавання за модулем m ( 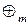 ); потужність
); потужність 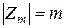 , отже, порядок групи
, отже, порядок групи 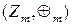 теж дорівнює m.
теж дорівнює m.
3. Множина 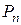 всіх підстановок з n елементів утворює групу відносно добутку; потужність
всіх підстановок з n елементів утворює групу відносно добутку; потужність 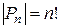 .
.
4. Множина 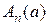 цілих степенів заданого числа
цілих степенів заданого числа 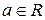 утворює абелеву групу. Справді:
утворює абелеву групу. Справді: 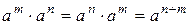 ,
, 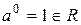 ,
, 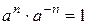 ,
, 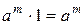 .
.
5. У комплексній площині 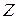 множина коренів степеня n з одиниці
множина коренів степеня n з одиниці 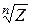 , де
, де 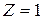 , утворює абелеву групу відносно звичайного множення (
, утворює абелеву групу відносно звичайного множення ( 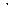 ). Справді,
). Справді, 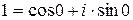 ,
, 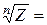
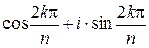 , n
, n 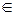 Z,
Z, 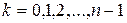 . Очевидно, що це моноїд. Доведемо, що для кожного кореня існує обернений елемент. Нехай
. Очевидно, що це моноїд. Доведемо, що для кожного кореня існує обернений елемент. Нехай 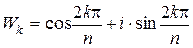 . Тоді
. Тоді 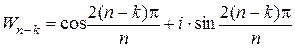 . Розглянемо їхній добуток, спочатку спростивши
. Розглянемо їхній добуток, спочатку спростивши 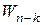 :
:
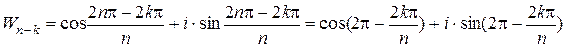 .
.
Звідси, в силу періодичності тригонометричних функцій, парності косинуса й непарності синуса, матимемо:
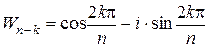 .
.
Тепер покажемо, що для всіх 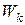 існують обернені елементи, а саме
існують обернені елементи, а саме 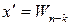 :
:
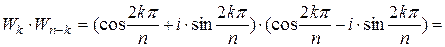
 .
.
Отже, множина коренів степеня 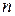 з одиниці
з одиниці 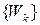 , де
, де 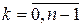 є абелевою групою відносно операції множення.
є абелевою групою відносно операції множення.
Для півгрупи А підмножину 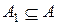 називають підпівгрупою, якщо
називають підпівгрупою, якщо 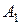 замкнута відносно бінарної операції
замкнута відносно бінарної операції 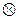 , тобто для будь-яких
, тобто для будь-яких 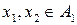 виконується:
виконується: 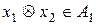 .
.
Розглянемо приклади кілець.
1. Множина Z цілих чисел утворює кільце відносно операцій додавання (+) й множення ( 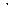 ).
).
2. Множина 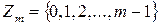 цілих невід’ємних лишків за модулем m утворює комутативне кільце з одиницею відносно операцій додавання (
цілих невід’ємних лишків за модулем m утворює комутативне кільце з одиницею відносно операцій додавання ( 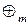 ) й множення (
) й множення ( 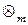 ) за модулем m (при цьому
) за модулем m (при цьому 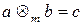 так, що
так, що 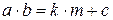 і
і 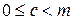 , де
, де 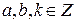 ,
, 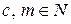 ).
).
Розглянемо приклади полів.
1. Множина R дійсних чисел із звичайними операціями додавання (+) й множення ( 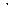 ) є полем і містить абелеві групи
) є полем і містить абелеві групи 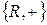 і
і 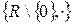 . Алгебричну структуру
. Алгебричну структуру 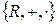 називають полем дійсних чисел.
називають полем дійсних чисел.
2. Множина Q раціональних чисел із звичайними операціями додавання (+) й множення ( 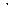 ) є полем.
) є полем.
3. Множина комплексних чисел 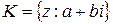 з операціями додавання (+) й множення (
з операціями додавання (+) й множення ( 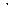 ) є полем.
) є полем.
1.8. Поняття векторного простору
Нехай задано множину 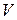 і поле
і поле 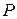 . На
. На 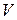 задано внутрішню (замкнену) бінарну операцію додавання (+) і операцію множення (
задано внутрішню (замкнену) бінарну операцію додавання (+) і операцію множення ( 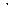 ) елементів множини
) елементів множини 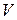 на елементи поля Р, результат якої належить
на елементи поля Р, результат якої належить 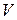 . Тоді множину
. Тоді множину 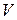 називають векторним просторомнад полем
називають векторним просторомнад полем 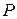 , а його елементи — векторамиза умови, що
, а його елементи — векторамиза умови, що 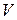 — абелева група відносно додавання і для будь-яких
— абелева група відносно додавання і для будь-яких 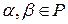 , а також будь-яких
, а також будь-яких 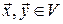 виконуються рівності:
виконуються рівності:
1) 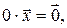 де
де 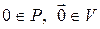 ;
;
2)  , де
, де 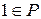 ;
;
3) 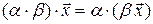 ;
;
4) 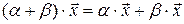 ;
;
5) 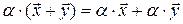 .
.
Вектор 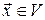 виду
виду 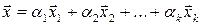 при будь-яких
при будь-яких 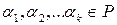 називають лінійною комбінацією векторів
називають лінійною комбінацією векторів 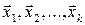 . Лінійна комбінація тривіальна(нульова), якщо всі елементи
. Лінійна комбінація тривіальна(нульова), якщо всі елементи 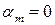 ,
, 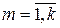 ; лінійна комбінація нетривіальна, якщо хоч би один з елементів
; лінійна комбінація нетривіальна, якщо хоч би один з елементів 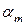 не дорівнює нулю.
не дорівнює нулю.
Вектори 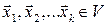 називають лінійно залежними, якщо існує їхня нетривіальна лінійна комбінація, рівна нульовому вектору, і лінійно незалежними, якщо тільки їхня тривіальна комбінація дорівнює нулю.
називають лінійно залежними, якщо існує їхня нетривіальна лінійна комбінація, рівна нульовому вектору, і лінійно незалежними, якщо тільки їхня тривіальна комбінація дорівнює нулю.
Якщо в 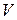 існують n лінійно незалежних векторів, а будь-які
існують n лінійно незалежних векторів, а будь-які 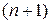 векторів із
векторів із 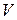 лінійно залежні, то
лінійно залежні, то 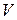 називають n-вимірним векторним простором, а число
називають n-вимірним векторним простором, а число 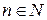 називають вимірністю векторного простору
називають вимірністю векторного простору 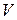 . Цей простір позначають
. Цей простір позначають 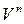 . Якщо у просторі
. Якщо у просторі 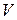 існує лінійно незалежна система з будь-якою кількістю векторів, то простір є нескінченно вимірним.
існує лінійно незалежна система з будь-якою кількістю векторів, то простір є нескінченно вимірним.
Систему n лінійно незалежних векторів 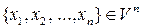 , заданих у певному порядку, називають базисом простору
, заданих у певному порядку, називають базисом простору 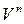 , якщо довільний елемент
, якщо довільний елемент 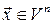 можна однозначно подати у вигляді нетривіальної лінійної комбінації цих векторів:
можна однозначно подати у вигляді нетривіальної лінійної комбінації цих векторів:
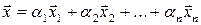 .
.
При цьому числа 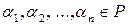 називають координатами вектора
називають координатами вектора 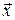 у базисі
у базисі  .
.
Зауважимо, що поле Р може бути, наприклад, полем дійсних чисел, або полем комплексних чисел, або якимось іншим полем. У таких випадках, відповідно, кажуть про дійсний векторний простір, комплексний векторний простір, векторний простір над полемР.
Приклад 1.12. а) Якщо 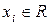 при
при 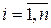 , то матимемо векторний простір
, то матимемо векторний простір 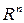 скінченних (n-вимірних) дійсних векторів
скінченних (n-вимірних) дійсних векторів 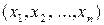 .
.
