Дадим определения пределов функции при

.

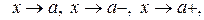
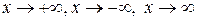Пусть функция 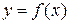определена в некоторой окрестности точки а, кроме, быть может, этой точки.

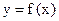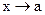Определение.Число А называется пределом функции при , если для каждого 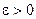найдётся такое d>0, что для всех 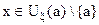выполняется неравенство 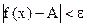, т. е.

.

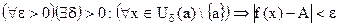(Обозначается 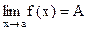или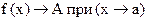

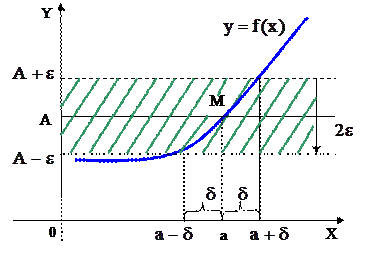
Рис.4

Определение. Число А называется пределом слева функции 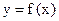при ,

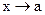если .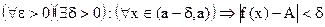

(Обозначается 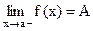или ).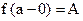

Определение . Число А называется пределом справа функции 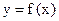при ,

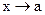если .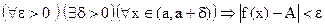

(Обозначается 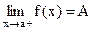или ).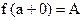

Теорема. 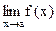существует в том и только в том случае, когда существуют пределы 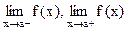, и они равны между собой.

Пример. .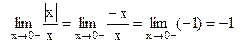

В этом примере рассматривается только 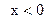, поэтому .

.

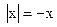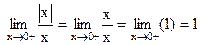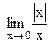не существует, поскольку .

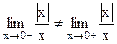Определение. Число А называется пределом функци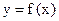и при 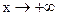, если для каждого e>0 найдётся такое число N , что при любом 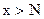выполняется 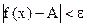, т. е.

.

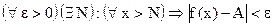(Обозначается ).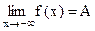

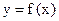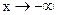Определение. Число А называется пределом функции при , если .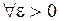

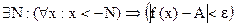(Обозначается .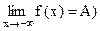

Определение. Число А называется пределом функци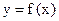и при 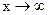, если 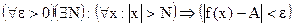. (Обозначается ).

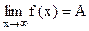Последнее определение подразумевает, что 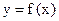определена в некотором интервале 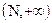, пятое определение подразумевает, что она определена в интервале 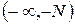, а из шестого определения следует, что она определена пр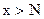и и 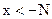, т. е. в промежутках .

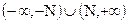Теорема. Предел 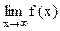существует в том и только в том случае, когда существуют 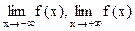и они равны между собой.

Примеры:

1. ;
2. 

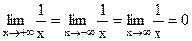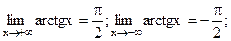
Докажем, что 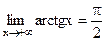. Для 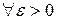возьмем 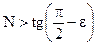, тогда при

.

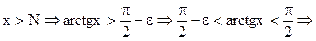
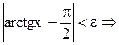
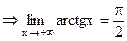Рис.5

Свойства функций и последовательностей, имеющих предел. Рассматриваемые ниже свойства справедливы для всех видов пределов функций и пределов последовательности. Однако для краткости будем формулировать их для одного предела (при ).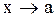

1) Предел постоянной функции (или последовательности) равен этой постоянной, т. е.

.

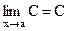2) Если предел функции (последовательности) существует, то он единствен.

Определение. Функция 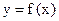называется ограниченной сверху в промежутке D, если найдётся такое число С, что для всех x принадлежащих D, 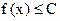. Если 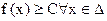, то такая функция называется ограниченной снизу в D.

Функция, ограниченная сверху и снизу в D, называется ограниченной в D. Если D не упоминается, то подразумевается, что D=R.

Примеры:

1) Функция 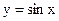ограничена, т. к. 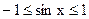для всех x.

2) Функция 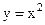ограничена снизу, но не сверху. На промежутке 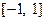она ограничена.

Определение. Последовательность 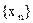называется ограниченной (сверху, снизу), если найдётся такое С, что для всех 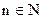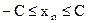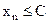, , (или , или ).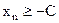

Примеры:

1. 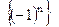– ограничена.

2. 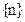– ограничена снизу.

3) Если функция 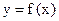имеет предел 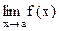, то она ограничена в некоторой окрестности точки a .

При существовании пределов 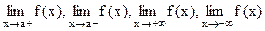функция ограничена в соответствующих интервалах

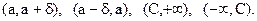
4) Любая последовательность, имеющая предел, ограничена.

Определение. Функция 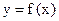называется неубывающей (возрастающей) в интервале

(а, 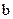), если для любых 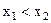из этого интервала выполняется неравенство

( ).

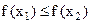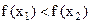Если 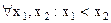, имеет место

( ),

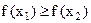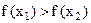то такая функция называется невозрастающей (убывающей) в (а, 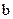). Такие функции называют монотонными на (а; ).

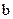Определение. Последовательность 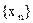называется неубывающей (невозрастающей), если для любых 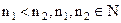выполняется

.

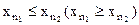Примеры:

1. Любая постоянная функция или последовательность не возрастает и не убывает.

Функция 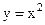монотонна, убывает на интервале (-¥,0) и возрастает на интервале (0,+¥).

Теорема. Пусть функция монотонно возрастает (убывает) на интервале (а, 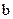) и ограничена сверху (снизу) на этом интервале числом С, тогда существует

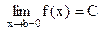
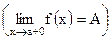и .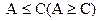

Здесь число 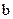может быть равным +¥, тогда рассматривается .

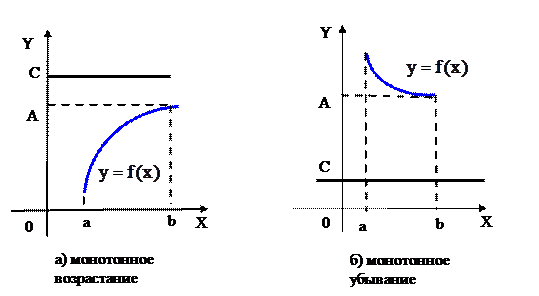
Рис.6

Если последовательность 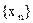монотонно возрастает (убывает) и ограничена сверху (снизу), то существует 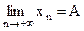и числ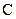о , что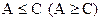

Аналогичное утверждение можно сформулировать для 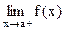и .

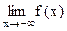Теорема. Пусть в некоторой окрестности точки 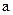, кроме этой точки, для функций 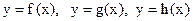выполняется соотношение 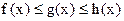и пусть пределы 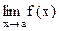и 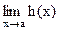существуют и равны между собой, 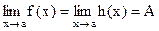. Тогда 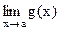также существует и равен ( см. рис 7).

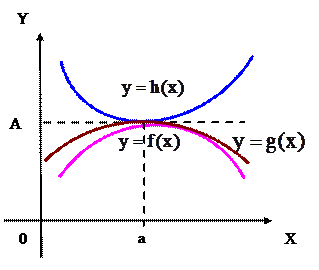Рис.7

Сформулируйте и докажите аналогичные утверждения для последовательностей.