Общее уравнение прямой на плоскости
Покажем, в первую очередь, что прямая задается на плоскости уравнением первого порядка
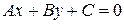 ,
,
где хотя бы один из коэффициентов 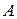 ,
, 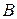 отличен от нуля. Пусть задано такое уравнение. Покажем, что оно определяет некоторую прямую на плоскости. Очевидно, что данное уравнение в силу линейности имеет хотя бы одно решение
отличен от нуля. Пусть задано такое уравнение. Покажем, что оно определяет некоторую прямую на плоскости. Очевидно, что данное уравнение в силу линейности имеет хотя бы одно решение 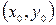 , т.е. существует хотя бы одна точка
, т.е. существует хотя бы одна точка 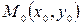 , координаты которой удовлетворяют этому уравнению:
, координаты которой удовлетворяют этому уравнению:
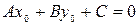 .
.
Вычитая из данного уравнения полученное равенство, будем иметь:
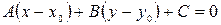 ,
,
эквивалентное данному уравнению. Покажем, что это уравнение определяет прямую на плоскости, проходящую через точку 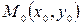 перпендикулярно вектору
перпендикулярно вектору 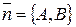 (
( 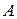 ,
, 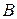 одновременно не равны нулю). В самом деле, если точка
одновременно не равны нулю). В самом деле, если точка 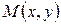 лежит на указанной прямой, то векторы
лежит на указанной прямой, то векторы 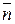 и
и 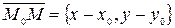 ортогональны и их скалярное произведение
ортогональны и их скалярное произведение
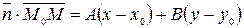
равно нулю. Если же точка 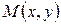 не лежит на указанной прямой, то ее координаты не удовлетворяют уравнению
не лежит на указанной прямой, то ее координаты не удовлетворяют уравнению 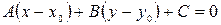 , ибо в этом случае векторы
, ибо в этом случае векторы 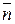 и
и 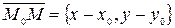 не ортогональны, и поэтому их скалярное произведение не может равняться нулю, т.е.
не ортогональны, и поэтому их скалярное произведение не может равняться нулю, т.е.
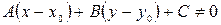 .
.
Итак, уравнение 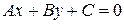 - уравнение прямой, и оно называется общим уравнением. Кроме того, мы доказали, что вектор
- уравнение прямой, и оно называется общим уравнением. Кроме того, мы доказали, что вектор 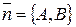 перпендикулярен этой прямой. Любой вектор, лежащий на прямой, перпендикулярной данной, будем называть вектором нормали.
перпендикулярен этой прямой. Любой вектор, лежащий на прямой, перпендикулярной данной, будем называть вектором нормали.
Общее уравнение прямой называется полным, если все его коэффициенты не равны нулю. Если хотя бы один из коэффициентов общего уравнения равен нулю, то это уравнение называется неполным. Рассмотрим все возможные виды неполных уравнений.
1) Пусть 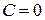 . Тогда получаем уравнение
. Тогда получаем уравнение
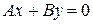 ,
,
которое определяет прямую, проходящую через начало координат.
2) Пусть 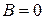 . Тогда получаем уравнение
. Тогда получаем уравнение
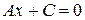
или
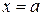 ,
,
где 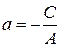 . Такое уравнение определяет прямую параллельную оси ординат, так как вектор нормали
. Такое уравнение определяет прямую параллельную оси ординат, так как вектор нормали 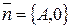 перпендикулярен этой оси.
перпендикулярен этой оси.
3) Пусть 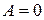 . Тогда получаем уравнение
. Тогда получаем уравнение
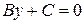
или
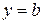 ,
,
где 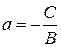 . Такое уравнение определяет прямую параллельную оси абсцисс, так как вектор нормали
. Такое уравнение определяет прямую параллельную оси абсцисс, так как вектор нормали 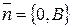 перпендикулярен этой оси.
перпендикулярен этой оси.
4) Пусть 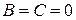 . Тогда получаем уравнение
. Тогда получаем уравнение
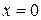 ,
,
определяющее ось ординат, так как это – прямая, параллельная оси ординат, и, проходящая через начало координат.
5) Пусть 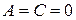 . Тогда получаем уравнение
. Тогда получаем уравнение
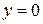 ,
,
определяющее ось абсцисс, так как это – прямая, параллельная оси абсцисс, и, проходящая через начало координат.
Рассмотрим полное уравнение прямой 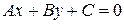 . Так как все коэффициенты этого уравнения не равны нулю, то это уравнение можно переписать в виде:
. Так как все коэффициенты этого уравнения не равны нулю, то это уравнение можно переписать в виде:
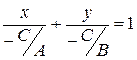 .
.
Если обозначить: 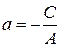 ,
, 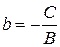 , то получаем следующий вид уравнения прямой:
, то получаем следующий вид уравнения прямой:
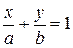 .
.
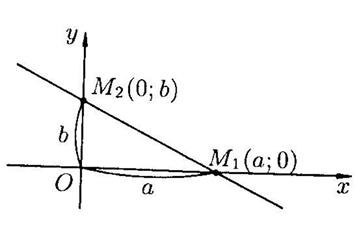 Такое уравнение называется уравнением в отрезках. Очевидно, что такая прямая проходит через точки
Такое уравнение называется уравнением в отрезках. Очевидно, что такая прямая проходит через точки 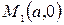 и
и 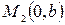 . Таким образом, коэффициенты
. Таким образом, коэффициенты 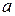 и
и 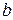 равны величинам отрезков, отсекаемых данной прямой на соответствующих координатных осях.
равны величинам отрезков, отсекаемых данной прямой на соответствующих координатных осях.
