Кривые второго порядка (31-40)

1) Уравнение вида

,

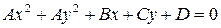
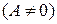которое характеризуется равенством коэффициентов при и и отсутствием произведения 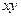, определяет на плоскости окружность, точку или пустое множество.

Разделив обе части уравнения на А и выделив из квадратных трехчленов полные квадраты, получим

.

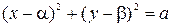Если 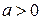, то это уравнение окружности с центром в точке и радиусом .

2) Уравнение

,

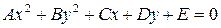
в котором коэффициенты и при и не равны, но имеют одинаковые знаки, и отсутствует произведение координат, задает на плоскости эллипс, оси которого параллельны осям координат, точку или пустое множество. Для эллипса после выделения полных квадратов данное уравнение приводится к виду

,

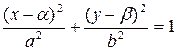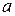где точка 2 центр, и 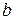2 полуоси эллипса.

3) 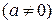– уравнение параболы, ось которой параллельна оси ;

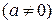– уравнение параболы, ось которой параллельна оси .

После выделения полного квадрата первое уравнение запишется в виде

,

второе –

.

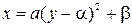Точки и 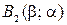– вершины первой и второй парабол соответственно.

4) Уравнение ,

определяет на плоскости гиперболу или две пересекающиеся прямые. Выделяя полные квадраты, для гиперболы данное уравнение приводится к виду:

,

где 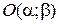– центр, – полуоси гиперболы.

Пример. Построить кривую .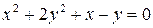

Решение. Это эллипс. Выделяем полные квадраты.

,

,

,

,

,

.

; , .

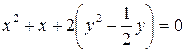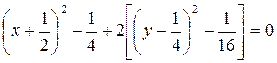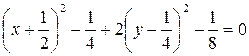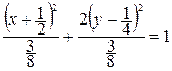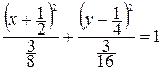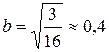Уравнение кривой в полярных координатах (41-50)

Чтобы в уравнении кривой перейти от полярных координат ,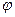

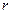
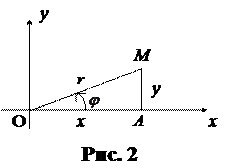к декартовым 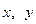, используйте формулы: 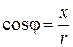, , 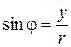, которые получаются из рассмотрения прямоуголь- ного треугольника ОАМ, изображенного на рис. 2.

Пример. Пусть задана кривая уравнением в полярных координатах

.

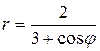Решение.

, , ,

, , .

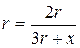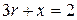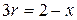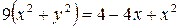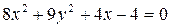– уравнение кривой в декартовых координатах (эллипс).

Комплексные числа (51-60)

Комплексным числом называется выражение вида 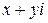, где 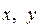– действительные числа, 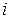– мнимая единица, удовлетворяющая условию .

Комплексное число 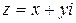изображается точкой плоскости или радиусом-вектором 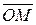этой точки (см. рис. 2). Из прямоугольного треугольника ОАМ получаются следующие формулы:

,

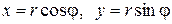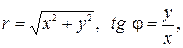
где 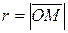– модуль числа 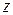, 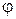– аргумент.

Запишем комплексное число 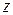в алгебраической, тригонометрической и показательной формах:

.

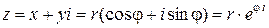Комплексные числа в алгебраической форме складываются и умножаются, как многочлены, причем

, ,

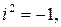
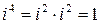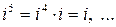
При делении комплексных чисел числитель и знаменатель надо умножить на число, сопряженное знаменателю, например:

.

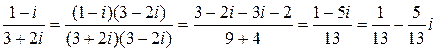Показательная функция

.

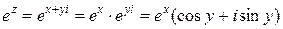Корень -й степени из комплексного числа

,

.

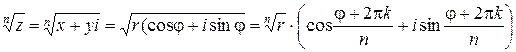Пример.Найти все корни уравнения .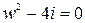

Решение.Из уравнения следует, что 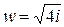. Пусть 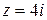. Это комп-

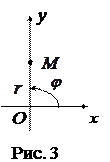лексное число изображено на рис. 3 точкой М (0; 4). Тогда модуль 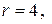а аргумент 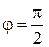. В триго- нометрической форме число z имеет вид:

	.

.

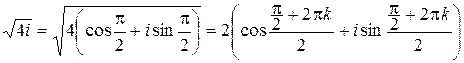Если 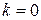, то .

Если , то .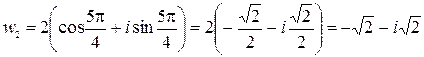

Ответ: .

Контрольная работа №2
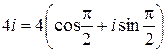