Матричная форма записи системы
Линейных уравнений
Вернемся к системе (1.1).
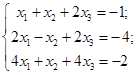 |
с матрицей коэффициентов А столбцом неизвестных Х и столбцом свободных членов В:
А =  ; Х = ; Х = 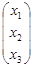 ; В = ; В =  . . |
Умножим матрицу А на столбец Х. Используя введенное правило умножения матрицы на столбец, получим
A×X =  ×
× 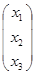 =
=  =
= 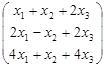 .
.
Из системы уравнений (1.1) следует, что первый элемент полученного столбца равен –1, второй равен –4, а третий равен –2. Матрицы, имеющие одинаковые размерности и равные элементы, по определению, считаются равными матрицами. Учитывая это определение равенства матриц, можем записать
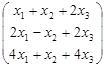 =
= 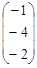 .
.
Отсюда следует, что систему (1.1) можно записать в виде
 ×
× 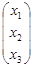 =
= 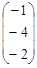 ,
,
или, с учетом обозначения матриц, в виде
| A×X = В. | (1.7) |
Запись системы в виде (1.7) называется матричной формой записи системы линейных уравнений.
Матричные обозначения в методе Гаусса
В разд.1.1 был разобран пример решения системы уравнений методом Гаусса. Обычно исключение неизвестных проводится обращением в ноль элементов матрицы системы и приведением ее к “треугольному” виду.
Пример 1.3
Решить систему уравнений
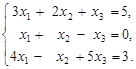
Решение
Выпишем матрицу системы и через разделительные черточки припишем к ней столбец правых частей уравнений.
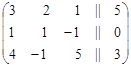 .
.
Такая матрица называется расширенной матрицей системы.
Со строками и столбцами расширенной матрицы можно производить преобразования, которые равносильны сложению уравнений системы, перестановке местами слагаемых в уравнениях и другим действиям, преобразующим данную систему к эквивалентной. Такими преобразованиями являются:
1) перестановка местами строк матрицы (эквивалентно перестановке местами уравнений системы);
2) перестановка местами столбцов “левой части” матрицы (эквивалентно перестановке слагаемых в уравнениях);
3) умножение всех элементов некоторой строки матрицы на число, неравное нулю (эквивалентно умножению уравнения на некоторое число);
4) прибавление к элементам некоторой строки соответствующих элементов другой строки (эквивалентно сложению двух уравнений системы).
Рассмотрим последовательность применения этих операций.
1. Процесс исключения удобно начать, когда ведущим элементом является единица. Для этого поменяем местами вторую строку с первой:
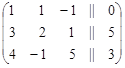 .
.
2. Оставляя первую строку без изменений, к элементам второй строки прибавим элементы первой строки, умноженные на –3, а к элементам третьей строки прибавим элементы первой строки, умноженные на – 4, расширенная матрица преобразуется к виду:
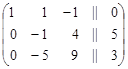 .
.
3. Ведущим элементом второго шага является –1 во второй строке и втором столбце. Первую и вторую строку оставим без изменений, а к третьей строке прибавим вторую строку, умноженную на –5:
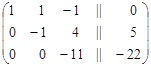 .
.
4. Теперь вторую строку умножим на –1, а третью – разделим на –11, тогда расширенная матрица будет иметь вид
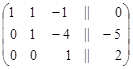 ,
,
которому соответствует преобразованная система уравнений:
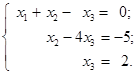
Последнее уравнение дает х3 = 2; подставляя это значение во второе уравнение, получаем х2 = 3 и, наконец, из первого уравнения находим х1= –1.
Таким образом, 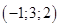 – решение системы.
– решение системы.
Пример 1.4
Решить систему линейных уравнений АХ = В методом Гаусса:
А= 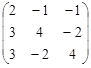 ; В =
; В = 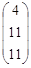 .
.
Решение
Для того чтобы на каждом шаге исключения ведущим элементом была единица, при решении этой системы производится перестановка столбцов матрицы 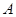 , поэтому сверху над столбцами указываются неизвестные, содержащиеся в этом столбце:
, поэтому сверху над столбцами указываются неизвестные, содержащиеся в этом столбце:
х1 х2 х3
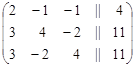 .
.
Поменяем местами первый и второй столбцы матрицы
х2 х1 х3
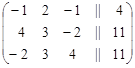 .
.
Ко второй строке прибавим первую строку, умноженную на 4, а к третьей строке прибавим первую строку, умноженную на –2, получим
х2 х1 х3
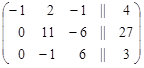 .
.
Поменяем местами вторую строку с третьей
х2 х1 х3
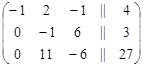 .
.
К третьей строке прибавим вторую строку, умноженную на 11, тогда расширенная матрица будет иметь вид
х2 х1 х3
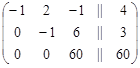 ,
,
которому соответствует преобразованная система уравнений:
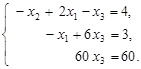
Последнее уравнение дает х3 = 1; подставляя это значение во второе уравнение, получаем х1 = 3 и, наконец, из первого уравнения находим х2 = 1. Решение системы 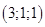 .
.
