Частные производные высших порядков
Пусть функция 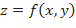 имеет первые частные производные
имеет первые частные производные 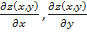 в точке
в точке 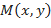 и в каждой точке некоторой окрестности точки
и в каждой точке некоторой окрестности точки 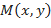 . Тогда частные производные от частных производных
. Тогда частные производные от частных производных 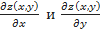 называются частными производными второго порядка от функции
называются частными производными второго порядка от функции 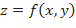 в точке
в точке 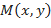 . Частные производные второго порядка обозначаются
. Частные производные второго порядка обозначаются 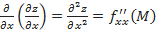 ;
; 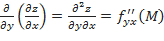 ;
;
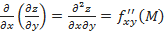 ;
; 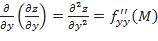 .
.
Если частные производные первого порядка непрерывны, то значение «смешанной» производной не зависит от порядка дифференцирования, т.е. 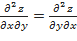 . Это положение распространяется и на частные производные более высокого порядка.
. Это положение распространяется и на частные производные более высокого порядка.
Пример №19 Найти вторые частные производные функции 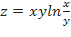 .
.
Решение:
Вначале находим частные производные первого порядка:
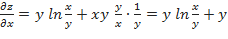 ;
; 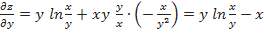 .
.
Далее находим
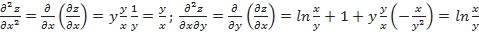 ;
;
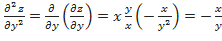 .
.
Пример №20 Проверить, что 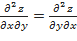 , если
, если 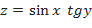 .
.
Решение:
Находим 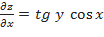 ;
; 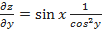 .
.
Далее, 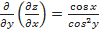 ;
; 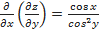 . Очевидно, что
. Очевидно, что 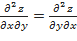 .
.
Задания:
1. Найти вторые частные производные от заданных функций:
а) 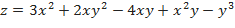 ;
;
b) 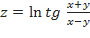 ;
;
c) 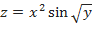 .
.
2. Проверить, что 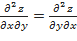 для функций:
для функций:
а) 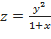 ;
;
b) 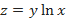 ;
;
c) 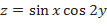 .
.
3. Показать, что функция 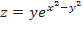 удовлетворяет уравнению
удовлетворяет уравнению
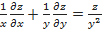 .
.
Экстремум функции двух переменных
Функция 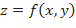 имеет максимум ( минимум) в точке
имеет максимум ( минимум) в точке 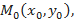 если для любой точки
если для любой точки 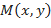 , находящейся в некоторой
, находящейся в некоторой 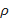 - окрестности точки
- окрестности точки 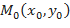 , выполняется условие
, выполняется условие 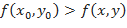
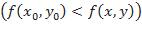 ;
;
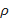 - окрестность можно представить множеством точек
- окрестность можно представить множеством точек 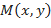 , координаты которых удовлетворяют условию
, координаты которых удовлетворяют условию 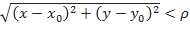 , где
, где 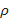 – положительное достаточно малое число.
– положительное достаточно малое число.
Максимумы и минимумы функции называются экстремумами, а 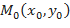 - экстремальной точкой.
- экстремальной точкой.
Необходимое условие экстремума: Если 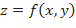 - дифференцируемая функция и достигает в точке
- дифференцируемая функция и достигает в точке 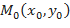 экстремума, то ее частные производные первого порядка в этой точке равны нулю:
экстремума, то ее частные производные первого порядка в этой точке равны нулю: 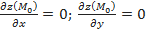 .
.
Точки, в которых частные производные первого порядка обращаются в ноль (или не существуют), называются критическими или стационарными. Исследование их на экстремум проводят с помощью достаточных условий существования экстремума функции двух переменных.
Пусть 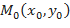 - стационарная точка функции
- стационарная точка функции 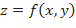 . Для ее исследования сначала вычисляют частные производные второго порядка в точке
. Для ее исследования сначала вычисляют частные производные второго порядка в точке 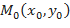 :
: 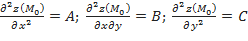 , а затем дискриминант
, а затем дискриминант 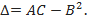 Тогда достаточные условия экстремума функции запишутся в следующем виде:
Тогда достаточные условия экстремума функции запишутся в следующем виде:
1) 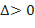 – экстремум есть, при этом, если
– экстремум есть, при этом, если 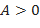 ( или
( или 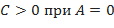 ), в точке
), в точке 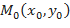 функция имеет минимум, а если
функция имеет минимум, а если 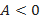 ( или
( или 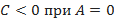 ) – максимум;
) – максимум;
2) 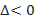 – экстремума нет;
– экстремума нет;
3) 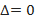 – требуются дополнительные исследования.
– требуются дополнительные исследования.
Условный экстремум
Рассмотрим функцию 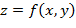 , определенную и дифференцируемую в области
, определенную и дифференцируемую в области 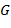 , координаты точек которой удовлетворяют системе уравнений связи
, координаты точек которой удовлетворяют системе уравнений связи 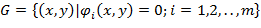 . В этой области нужно найти такую точку
. В этой области нужно найти такую точку 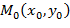 , чтобы выполнялось условие
, чтобы выполнялось условие 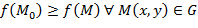 . Такие задачи называются задачами отыскания условного экстремума функции
. Такие задачи называются задачами отыскания условного экстремума функции 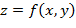 .
.
Для отыскания условного экстремума исследуется на обычный экстремум функция Лагранжа 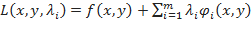 .
.
Необходимые условия экстремума функции Лагранжа имеют вид:
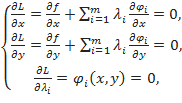
Из этой системы 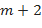 уравнений с
уравнений с 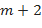 неизвестными находят значения неизвестных
неизвестными находят значения неизвестных 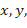
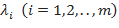 . Числа
. Числа 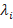 называются коэффициентами Лагранжа.
называются коэффициентами Лагранжа.
Пример №21 Найти экстремумы функции 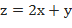 при условии
при условии 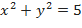 .
.
Решение:
Составляем функцию Лагранжа: 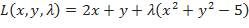 .
.
Находим частные производные и составляем необходимые условия экстремума функции Лагранжа:
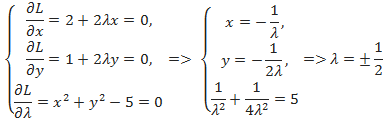
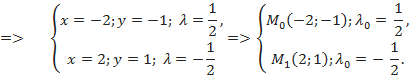
В данном случае 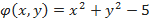 .
.
Для исследования на экстремум в полученных критических точках вычисляем значения 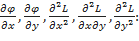
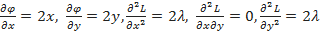 и составляем определитель:
и составляем определитель:
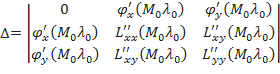 .
.
Если 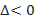 , то
, то 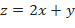 имеет в точке
имеет в точке 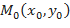 условный максимум, если
условный максимум, если 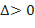 – условный минимум.
– условный минимум.
Итак, 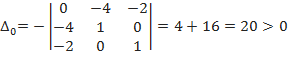 , следовательно, в точке
, следовательно, в точке 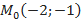 условный минимум,
условный минимум, 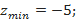
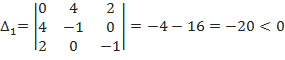 , следовательно, в точке
, следовательно, в точке 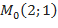 условный максимум,
условный максимум, 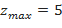 .
.
Задания:
- Найти экстремумы функций
а) 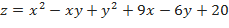 ;
;
b) 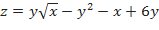 ;
;
c) 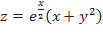 .
.
2. Найти условные экстремумы функций:
а) 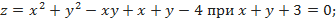
b) 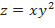 при
при  ;
;
c) 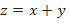 при
при 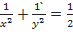
Типовые примеры.
Задание 1.
Найти область определения функции z= 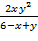 и её частные производные.
и её частные производные.
Решение.
Областью определения функции z= 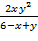 является множество точек плоскости, за исключением точек, удовлетворяющих равенству 6-х+у=0; т.е. точек, лежащих на прямой у=х-6.
является множество точек плоскости, за исключением точек, удовлетворяющих равенству 6-х+у=0; т.е. точек, лежащих на прямой у=х-6.
Найдём частные производные функции z. При нахождении z’x функция z дифференцируется по х, в предположении, что у=const.
z’x= 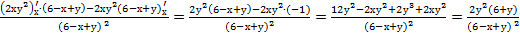
При нахождении z’y функция z дифференцируется по у, в предположении, что х=const
z’y= 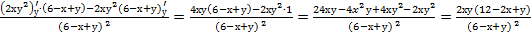
Задание 2.
Дана функция z=х  у+х
у+х 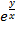 . Показать, что х
. Показать, что х 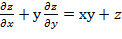
Решение.
Найдём частные производные функции z.
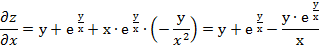
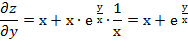
Подставим найденные производные в заданное выражение.
Х 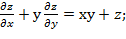
x(у+е 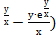 +у(х+е
+у(х+е 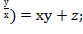
ху+хе 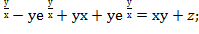
2ху+хе 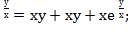
2ху+хе 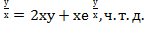
Задание 3.
Найти частные производные и частные дифференциалы функции z=ctg 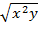
Решение.
Найдём частные производные:
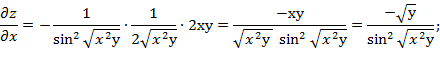
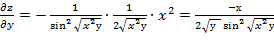 ;
;
Найдём частные дифференциалы.
dz 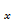 =
= 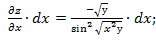
dz 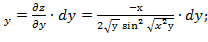
Задание 4.
Вычислить значения частных производных f' 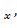 f’
f’ 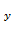 , f’
, f’ 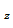 в точке М
в точке М 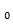 (1;
(1; 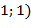 для функции
для функции 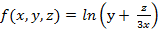
f' 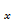 =
= 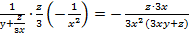 =-
=- 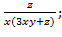
f’ 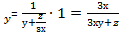 ;
;
f’ 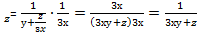 ;
;
f' 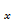 (М
(М 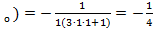 ;
;
f' 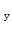 (М
(М 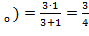 ;
;
f' 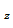 (М
(М 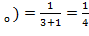
Задание 5.
Найти полный дифференциал функции z=ln(х cos 2y)
Решение.
Полный дифференциал функции определяется формулой
dz= 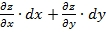
Найдём частные производные функции
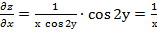
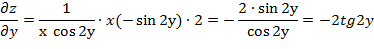
Полный дифференциал
dz= 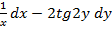
Задание 6.
Вычислить значение производной сложной функции z= 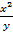 , где х=е
, где х=е 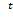 ; у=2-е
; у=2-е 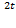 , при t
, при t 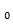 =0.
=0.
Решение.
Производная сложной функции z=z(х;у), где х=х(t); у=у(t) может быть вычислена по формуле
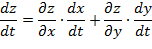
Найдём все производные:
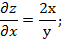
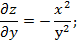

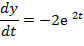
Тогда
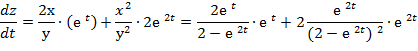
Найдём значение производной 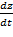 в точке t
в точке t 
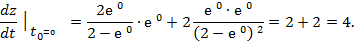
Задание7.
Вычислить значения частных производных неявной функции
е 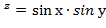 в точке М
в точке М 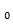 (
( 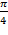 ;
; 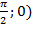
Решение.
Если функция z задана неявно, т.е. в виде уравнения F(x;у;z)=0, то частные производные этой функции могут быть заданы по формулам:
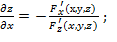
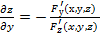 ;
;
Нам задана неявная функция
е 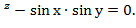
F 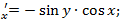 F
F 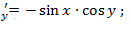 F
F 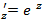
Следовательно
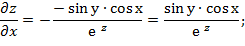
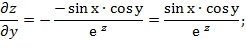
Найдём производные в точке М 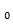 (
( 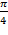 ;
; 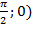
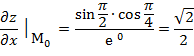
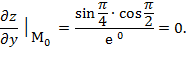
Задание 8.
- Найти уравнения касательной плоскости и нормали к поверхности
S: z= 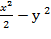 в точке М
в точке М 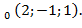
Решение.
Если уравнение поверхности задано в явной форме z=f(x,у), то уравнение касательной плоскости в точке М 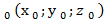 имеет вид
имеет вид
z- 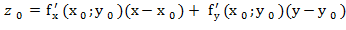 .
.
Уравнение нормали
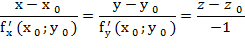
Найдём частные производные данной функции и их значения в точке М 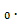
f 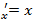 (f
(f 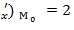
f 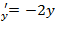 (f
(f 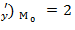
Отсюда, применяя формулы, будем иметь
z-1=2(x-2)+2(y+1) или 2х+2у-z-1=0 – уравнение касательной плоскости и
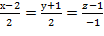 - уравнение нормали.
- уравнение нормали.
- Найти уравнения касательной плоскости и нормали к поверхности
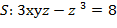 в точке М
в точке М 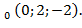
Решение.
Если уравнение поверхности задано в неявной форме F (x,y,z)=0, то уравнение касательной плоскости и нормали будут иметь вид
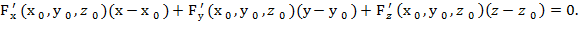
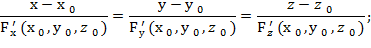
Найдём частные производные функции F (x,y,z) и их значения в точке М 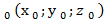
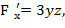
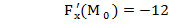
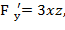
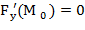
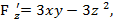
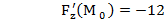
Следовательно уравнение касательной плоскости:
-12(х-0)+0(у-2)-12(z+2)=0 или х+z+2=0
Уравнение нормали
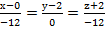 или
или 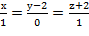
Задание 9.
Найти градиент функции Z= 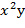 в точке М
в точке М 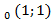
Решение.
Градиентом функции z=f(x,y) называется вектор, проекциями которого на координатные оси являются соответствующие частные производные данной функции.
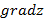 =
= 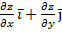
Найдём частные производные функции z и их значения в точке М 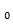
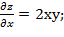
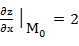
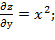
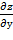
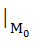 = 1
= 1
Следовательно, gradz=2 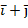
Задание 10.
Исследовать на экстремум функцию z= 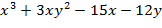
Решение.
Найдём частные производные:
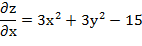
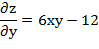
Используя необходимое условие экстремума:
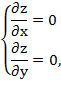
Составим систему уравнений
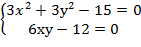
Решив эту систему найдём четыре стационарные точки.
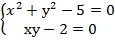
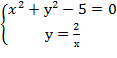
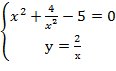
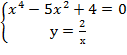
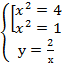
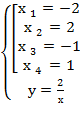
Стационарные точки М 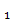 (-2;-1); М
(-2;-1); М 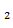 (2;1); М
(2;1); М 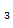 (-1;-2); М
(-1;-2); М  (1;2)
(1;2)
Найдём производные второго порядка
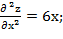
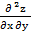 =6у;
=6у; 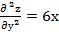
И составим дискриминант ∆=А 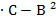 для каждой стационарной точки
для каждой стационарной точки
1) Для точки М 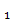 : А=
: А= 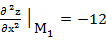 ; В=
; В= 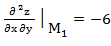 ; С=
; С= 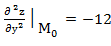
∆=А 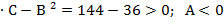 .
.
В точке М 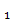 функция имеет максимум, равный z
функция имеет максимум, равный z 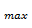 =-8-6+30+12=28
=-8-6+30+12=28
2) Для точки М 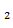 : А=12; В=6; С=12;
: А=12; В=6; С=12;
∆=144-36>0; А>0.
В точке М 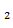 функция имеет минимум, равный z
функция имеет минимум, равный z 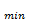 =8+6-30-12=-28
=8+6-30-12=-28
3) Для точки М 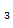 : А=-6; В=-12; С=-6;
: А=-6; В=-12; С=-6;
∆=36-144<0. Экстремума нет
4) Для точки М  : А=6; В=12; С=6;
: А=6; В=12; С=6;
∆=36-144<0. Экстремума нет
Расчетные задания.
Задание 1.
Найти область определения указанных функций и частные производные.
- z=
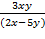 2. z=arcsin (x-y)
2. z=arcsin (x-y)
3. z= 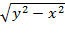 4. z=
4. z= 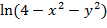
5. z= 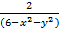 6. z=
6. z= 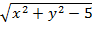
7. z=arccos (x+y) 8. z= 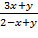
9. z= 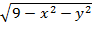 10. z=
10. z= 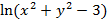
11. z= 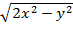 12. z=
12. z= 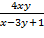
13. z= 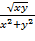 14. z=arcsin
14. z=arcsin 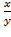
15. z= 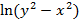 16. z=
16. z= 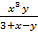
17. z=arccos (x+2y) 18. z= arcsin (2x-y)
19. z= 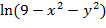 20. z=
20. z= 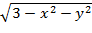
21. z= 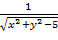 22. z=
22. z= 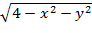
23. z= 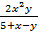 24. z=
24. z= 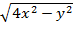
25. z= 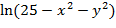 26. z= arcsin (3x-y)
26. z= arcsin (3x-y)
27. z= 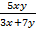 28. z=
28. z= 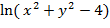
29. z= 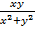 30. z=
30. z= 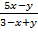
Задание 2.
1. Дана функция z= 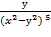 . Показать, что
. Показать, что 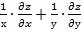 =
= 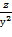
2. Дана функция z=х 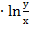 . Показать, что
. Показать, что 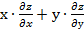 =z
=z
3. Дана функция z=(  tg
tg 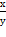 . Показать, что
. Показать, что 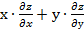 =2z
=2z
4. Дана функция z=arcsin 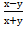 . Показать, что
. Показать, что 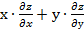 =0
=0
5. Дана функция z= 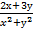 . Показать, что
. Показать, что 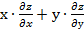 =-z
=-z
6. Дана функция z= 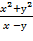 . Показать, что
. Показать, что 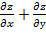 =
= 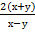
7. Дана функция 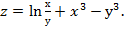 Показать, что
Показать, что 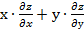 =3(
=3( 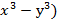
8. Дана функция z 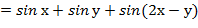 . Показать, что
. Показать, что 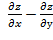 =
= 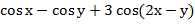
9. Дана функция 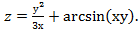 Показать, что
Показать, что 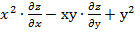 =0
=0
10. Дана функция 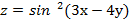 . Показать, что
. Показать, что 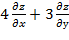 =0
=0
11. Дана функция 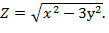 Показать, что 3у
Показать, что 3у  =0
=0
12. Дана функция 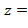 tg
tg 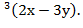 Показать, что 3у
Показать, что 3у 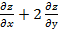 =0
=0
13. Дана функция 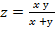 . Показать, что
. Показать, что 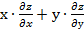 =z
=z
14. Дана функция 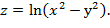 Показать, что
Показать, что 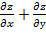 =
= 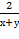
15. Дана функция 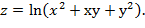 Показать, что
Показать, что 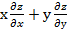 =2
=2
16. Дана функция 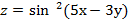 . Показать, что
. Показать, что 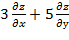 =0
=0
17. Дана функция 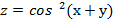 . Показать, что
. Показать, что 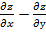 =0
=0
18. Дана функция 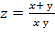 . Показать, что
. Показать, что 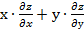 =-z
=-z
19. Дана функция 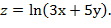 Показать, что
Показать, что 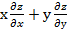 =1
=1
20. Дана функция 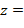 arc
arc 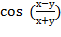 . Показать, что
. Показать, что 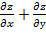 =-
=- 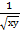
21. Дана функция 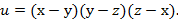 Показать, что
Показать, что 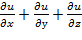 =0
=0
22. Дана функция 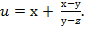 Показать, что
Показать, что 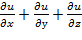 =1
=1
23. Дана функция 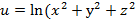 ). Показать, что
). Показать, что 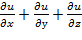 =2
=2
24. Дана функция 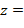 у
у 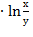 . Показать, что
. Показать, что 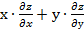 =z+2у
=z+2у
25. Дана функция 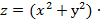 tg
tg 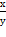 . Показать, что
. Показать, что 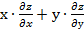 =2z
=2z
26. Дана функция 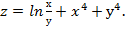 Показать, что
Показать, что 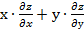 =4(
=4( 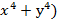
27. Дана функция 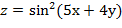 . Показать, что
. Показать, что 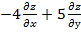 =0
=0
28. Дана функция 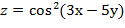 . Показать, что
. Показать, что 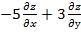 =0
=0
29. Дана функция 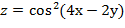 . Показать, что
. Показать, что 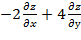 =0
=0
30. Дана функция 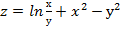 . Показать, что
. Показать, что 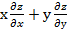 =2(
=2( 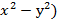
Задание 3.
Найти частные производные и частные дифференциалы следующих функций















Задание 4.
Вычислить значения частных производных f 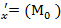 , f
, f 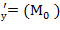 , f
, f 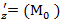 для данной функции f(х,у,z) в точке
для данной функции f(х,у,z) в точке 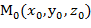
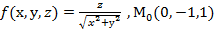
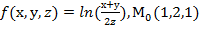
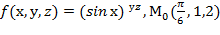
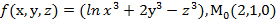
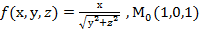
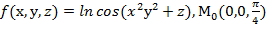
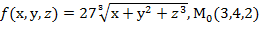
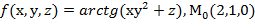
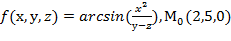
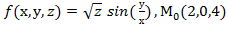
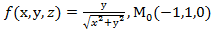
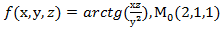
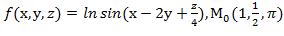
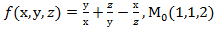
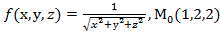
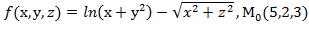
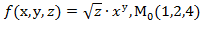
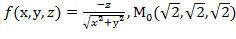
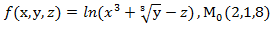
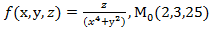
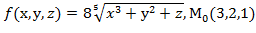
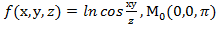
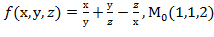
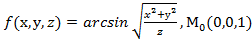
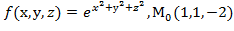
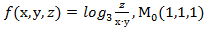
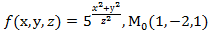
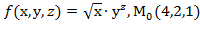
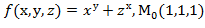
30. 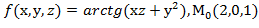
Задание 5.
Найти полные дифференциалы указанных функций
1. 














Задание 6.
Вычислить значение производной сложной функции z=z(х,у) где 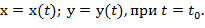
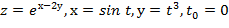
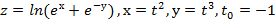
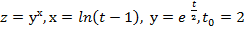
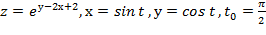
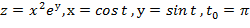
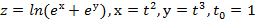
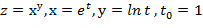
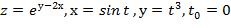
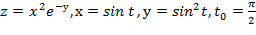
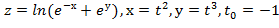
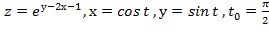
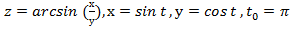
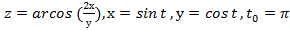
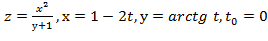
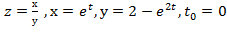
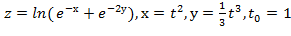
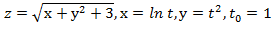
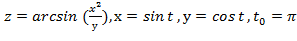
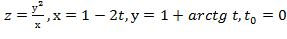
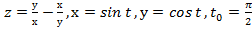
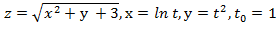
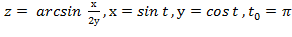
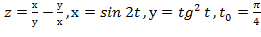
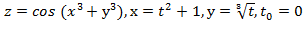
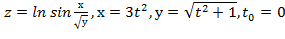
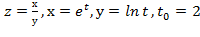
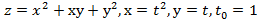
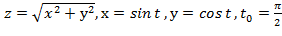
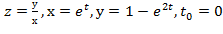
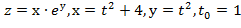
Задание 7.
Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке