Задача 5. Кручение вала

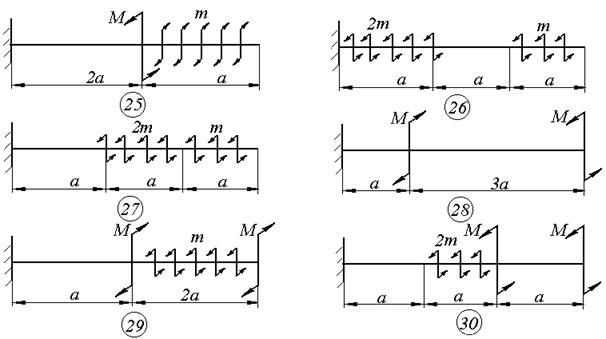
К стальному валу круглого поперечного сечения (см. схемы к задаче 5) приложены сосредоточенный момент М и распределённый момент m необходимо:

1. Составить аналитические выражения для определения внутреннего крутящего;

2. По полученным выражениям построить эпюру крутящего момента;

3. Из условия прочности по касательным напряжениям определить диаметр поперечного сечения;

4. Построить эпюру углов закручивания.

Численные значения приведены в таблице 3.1.

Таблица 3.1

№ варианта	М, кНм	m, кНм/м	а, м
	20	90	0,8
	40	70	0,9
	50	60	1
	60	50	1,1
	70	10	1,2
	80	20	0,5
	10	70	0,8
	20	60	0,7
	50	70	1,3
	30	80	1

Принять для всех валов следующие соотношения: , .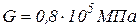

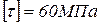Схемы к задаче 5

Схемы к задаче 5

Пример решения задачи 5

Для стального вала круглого поперечного сечения (рис. 3.1,а) необходимо:

1. Построить эпюру крутящего момента;

2. Из условия прочности по касательным напряжениям определить диаметр поперечного сечения и построить эпюру углов закручивания.

Дано: М=50кНм; m=10кНм/м; а=1м;

Решение

1. Для определения внутренних усилий в стержне пользуются методом сечений. Для этого стержень рассекают плоскостью в произвольном сечении z. Влияние любой из отброшенных частей стержня можно заменить только одним внутренним усилием – крутящим моментом 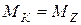. Для его определения составляют уравнение равновесия оставшейся части. Таким образом, крутящий момент определяется как сумма скручивающих нагрузок приложенных к одной из его частей. Крутящий момент будем считать положительным, если при взгляде на сечение со стороны внешней нормали он стремится повернуть оставшуюся часть стержня против хода часовой стрелки.

Пользуясь методом сечений, составим аналитические уравнения для определения крутящего момента:

Участок 1

;

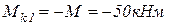Участок 2

;

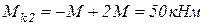Участок 3

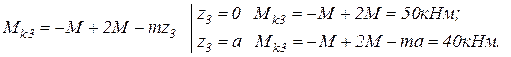
По найденным значениям строим эпюру крутящего момента (рис.3.1,б ).

2. Из условия прочности по касательным напряжениям найдём диаметр поперечного сечения вала:

;

где 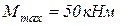- максимальный крутящий момент по модулю;

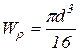- полярный момент сопротивления круглого сечения.

Подставляя полярный момент сопротивления в условие прочности, будем иметь:

,

Рис. 3.1 Схема к примеру решения задачи5

отсюда найдём диаметр вала:

.

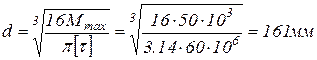3. Зная диаметр вала, найдём углы закручивания по следующей формуле:

,

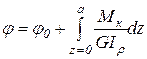где 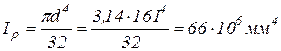- полярный момент инерции.

Определим углы закручивания в точках А, В, С и Д идя от заделки (рис.3.1,а):

;

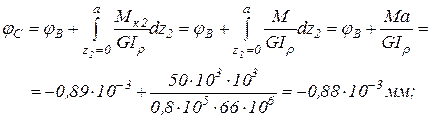
По найденным значениям строим эпюру углов закручивания (рис. 3.1,в).

Рекомендуемая литература

1. Феодосьев В. И. Сопротивление материалов: Учебник для студ-ов высш.техн.учеб.зав./ В.И.Феодосьев. – 10-е изд., перераб. и доп. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 588 с.

2. Писаренко Г.С. Сопротивление материалов /Г. С. Писаренко, В. А. Агарев, А. Л. Квитка, В.Г. Попков, Э. С. Уманский.- Киев: Высш. шк., 1986. – 776 с.

3. Александров А. В. и др. Сопротивление материалов: Учебник для ст-тов вузов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова. – 2-е изд., испр. – М.: Высшая школа, 2000. – 559 с.

4. Чеканов И.А. Сопротивление материалов: учеб. пособие / Чеканов И.А. - Красноярск: Изд-во КрасГАУ, 2005,

5. Миролюбов И.Н. и др. Пособие к решению задач по сопротивлению материалов. М., Высшая школа, 1974, - 392 с.

6. Беляев Н.М. Сопротивление материалов. – 15-е издание. – М, 1976. – 607 с.