Теоретическое обоснование. Вид нагружения бруса, при котором в его поперечных сечениях возникает только один
Вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – нормальная сила 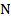 , называется растяжением или сжатием. Прямой брус, работающий на растяжение (сжатие), называется стержнем.
, называется растяжением или сжатием. Прямой брус, работающий на растяжение (сжатие), называется стержнем.
 Брус растянут, если внешние силы
Брус растянут, если внешние силы 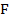 , приложенные к его концам, действуют вдоль оси бруса и направлены в стороны от бруса. При действии осевых нагрузок
, приложенные к его концам, действуют вдоль оси бруса и направлены в стороны от бруса. При действии осевых нагрузок 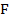 , направленных к брусу, он сжат.
, направленных к брусу, он сжат.

Известно, что под действием внешних сил возникают внутренние силы упругости. Их надо определить. Для этого используется метод сечений, который позволяет определить величину внутреннего силового фактора в сечении, но не дает возможности установить закон распределения внутренних сил. Данный метод заключается в мысленном рассечении тела плоскостью и рассмотрении равновесия любой из отсеченных частей.
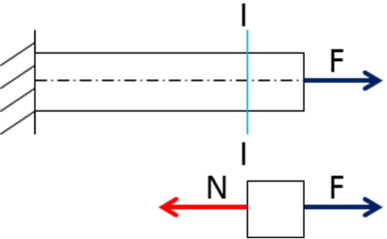
Метод состоит из четырех операций, которые могут быть последовательно записаны начальными буквами своих названий –РОЗУ (разрезаем, отбрасываем, заменяем, уравновешиваем):
· мысленно разрезаем интересующий нас сечением брус на две части, например левую или правую;
· одну из частей, безразлично какую, отбрасываем и рассматриваем оставшуюся (левую);
· заменяем действие отброшенной части на оставшуюся системой сил упругости, непрерывно распределенной по сечению, приводим к главному вектору и главному моменту;
· так как отсеченная часть должна находиться в равновесии, то внутренние силы определяются из условия равновесия, составленных для рассматриваемой части тела, т. е. уравновешиваемсистему сил.
Продольная сила в произвольном поперечном сечении бруса числено равна алгебраической сумме проекций внешних сил, расположенных по одну сторону сечения, т.е.  . Растягивающие (направленные от сечения) продольные силы будем считать положительными, та сжимающие (направленные к сечению)- отрицательными.
. Растягивающие (направленные от сечения) продольные силы будем считать положительными, та сжимающие (направленные к сечению)- отрицательными.
При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле 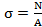 ,
,
где 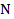 - продольная сила;
- продольная сила;  - площадь поперечного сечения.
- площадь поперечного сечения.
Для наглядного изображения распределения вдоль оси бруса продольных сил и нормальных напряжений строят графики, называемые эпюрами. Знаки как в математике. Ось эпюры параллельна оси бруса; эпюра штрихуется перпендикулярно оси бруса.

Абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине и обратно пропорционально жесткости сечения бруса

Для бруса, имеющего несколько участков, отличающихся материалом, размерами поперечного сечения, продольной силой , изменение длины всего бруса равно алгебраической сумме удлинений и укорочений отдельных участков: 
При растяжении (сжатии) бруса его поперечные сечения перемещаются в направлении оси. Перемещения являются следствием деформаций. Перемещение произвольного сечения бруса равно изменению длины участка, заключенного между этим сечением и заделкой
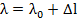
Если начальное сечение закреплено, то 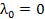
Вариант А Двухступенчатый стальной брус нагружен силами 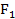 и и 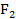 . Построить эпюры продольных сил, нормальных напряжений и перемещений. Определить полное абсолютное удлинение (укорочение) бруса. Принять: . Построить эпюры продольных сил, нормальных напряжений и перемещений. Определить полное абсолютное удлинение (укорочение) бруса. Принять: 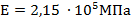 | Вариант Б Трехступенчатый стальной брус, длина ступеней которого указана на рисунке, нагружен силами 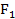 и и 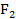 . Построить эпюры продольных сил, нормальных напряжений и перемещений. Определить полное абсолютное удлинение (укорочение) бруса. Принять: . Построить эпюры продольных сил, нормальных напряжений и перемещений. Определить полное абсолютное удлинение (укорочение) бруса. Принять: 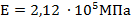 |
ЗАДАНИЕ
ЗАДАЧА


| вар | № схемы |  | 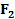 | 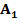 |  |  | вар | № схемы |  | 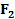 | 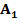 |  |  | |||||
| кН | 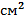 | кН | 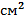 | |||||||||||||||
| 4,0 | 1,2 | 2,5 | 3,5 | 3,2 | 2,5 | |||||||||||||
| 4,5 | 1,5 | 3,8 | 2,8 | 2,1 | 1,6 | |||||||||||||
| 3,2 | 0,9 | 2,4 | 2,5 | 1,8 | 1,2 | |||||||||||||
| 6,0 | 2,0 | 4,2 | 10,4 | 3,2 | 2,6 | 2,1 | ||||||||||||
| 2,2 | 0,5 | 1,5 | 27,2 | 50,2 | 4,0 | 3,4 | 2,3 | |||||||||||
| 2,4 | 0,8 | 1,2 | 13,8 | 1,0 | 2,0 | 2,5 | ||||||||||||
| 4,2 | 1,5 | 2,8 | 4,8 | 28,8 | 1,2 | 2,5 | 3,0 | |||||||||||
| 3,4 | 1,0 | 2,2 | 7,0 | 21,5 | 1,4 | 2,8 | 3,0 | |||||||||||
| 4,8 | 1,4 | 3,6 | 17,6 | 43,2 | 1,6 | 3,0 | 3,2 | |||||||||||
| 5,4 | 2,5 | 4,0 | 9,9 | 22,7 | 1,8 | 3,2 | 3,5 | |||||||||||
| 3,0 | 8,4 | 0,4 | 0,2 | 0,6 | 17,0 | 51,0 | 2,0 | 3,5 | 4,0 | |||||||||
| 4,2 | 9,0 | 0,35 | 0,3 | 0,6 | 23,1 | 40,5 | 2,2 | 3,8 | 4,2 | |||||||||
| 4,8 | 10,0 | 0,64 | 0,4 | 0,8 | 12,0 | 39,0 | 2,4 | 4,0 | 4,5 | |||||||||
| 5,0 | 9,8 | 0,90 | 0,5 | 1,0 | 39,0 | 63,0 | 2,6 | 4,5 | 4,8 | |||||||||
| 7,2 | 15,0 | 1,0 | 0,6 | 1,5 | 39,2 | 80,8 | 2,8 | 5,0 | 5,2 | |||||||||
| 5,6 | 8,6 | 1,2 | 0,7 | 2,0 | 4,5 | 12,0 | 1,5 | 2,5 | 2,0 | |||||||||
| 7,2 | 14,0 | 1,5 | 0,8 | 2,4 | 7,2 | 17,4 | 1,8 | 2,8 | 2,0 | |||||||||
| 14,4 | 14,4 | 2,0 | 0,9 | 2,5 | 8,0 | 18,8 | 1,6 | 2,2 | 1,8 | |||||||||
| 9,0 | 22,0 | 1,5 | 1,0 | 3,0 | 8,4 | 20,4 | 1,4 | 2,0 | 1,5 | |||||||||
| 14,4 | 28,0 | 2,0 | 1,2 | 3,2 | 15,0 | 35,0 | 2,0 | 3,0 | 2,5 | |||||||||
| 3,1 | 2,0 | 1,5 | 12,0 | 16,4 | 2,1 | 3,0 | 2,4 | |||||||||||
| 3,0 | 2,4 | 2,0 | 14,3 | 29,3 | 2,2 | 3,0 | 2,5 | |||||||||||
| 3,5 | 2,8 | 2,2 | 13,3 | 24,8 | 1,9 | 2,8 | 2,3 | |||||||||||
| 3,0 | 2,5 | 1,8 | 9,2 | 22,2 | 2,3 | 3,2 | 2,5 | |||||||||||
| 3,6 | 3,0 | 2,4 | 21,6 | 45,6 | 2,4 | 3,5 | 3,0 | |||||||||||
| вар | № схемы |  | 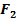 |  | 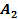 | 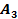 | вар | № схемы |  | 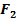 |  | 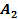 | 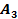 | |||||
| кН | 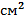 | кН | 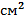 | |||||||||||||||
| 1,6 | 3,8 | 0,4 | 0,2 | 0,6 | 10,8 | 27,7 | 2,0 | 3,5 | 4,0 | |||||||||
| 3,6 | 6,6 | 0,35 | 0,3 | 0,6 | 15,4 | 18,8 | 2,2 | 3,8 | 4,2 | |||||||||
| 6,2 | 9,4 | 0,64 | 0,4 | 0,8 | 7,4 | 18,6 | 2,4 | 4,0 | 4,5 | |||||||||
| 3,75 | 8,0 | 0,9 | 0,5 | 1,0 | 11,7 | 18,9 | 2,6 | 4,5 | 4,8 | |||||||||
| 9,6 | 16,8 | 1,0 | 0,6 | 1,5 | 33,6 | 16,4 | 2,8 | 5,0 | 5,2 | |||||||||
| 9,8 | 4,9 | 1,2 | 0,7 | 2,0 | 12,0 | 30,0 | 1,5 | 2,5 | 2,0 | |||||||||
| 12,0 | 4,0 | 1,5 | 0,8 | 2,4 | 10,8 | 30,8 | 1,8 | 2,8 | 2,0 | |||||||||
| 11,7 | 5,0 | 2,0 | 0,9 | 2,5 | 12,8 | 34,8 | 1,6 | 2,2 | 1,8 | |||||||||
| 13,5 | 4,5 | 1,5 | 1,0 | 3,0 | 11,0 | 24,7 | 1,4 | 2,0 | 1,5 | |||||||||
| 18,0 | 7,2 | 2,0 | 1,2 | 3,2 | 22,4 | 2,4 | 2,0 | 3,0 | 2,5 | |||||||||
| 15,0 | 10,0 | 4,0 | 1,2 | 2,5 | 18,9 | 45,3 | 2,1 | 3,0 | 2,4 | |||||||||
| 18,3 | 30,5 | 4,5 | 1,5 | 3,8 | 30,8 | 15,3 | 2,2 | 3,0 | 2,5 | |||||||||
| 9,9 | 19,8 | 3,2 | 0,9 | 2,4 | 22,8 | 4,4 | 1,9 | 2,8 | 2,3 | |||||||||
| 28,0 | 8,0 | 6,0 | 2,0 | 4,2 | 36,8 | 11,8 | 2,3 | 3,2 | 2,5 | |||||||||
| 4,5 | 20,0 | 2,2 | 0,5 | 1,5 | 29,6 | 5,6 | 2,4 | 3,5 | 3,0 | |||||||||
| 8,4 | 15,0 | 2,4 | 0,8 | 1,2 | 16,8 | 34,8 | 2,0 | 3,1 | 1,5 | |||||||||
| 12,0 | 24,0 | 4,2 | 1,5 | 2,8 | 12,0 | 42,0 | 2,4 | 3,0 | 2,0 | |||||||||
| 16,2 | 5,2 | 3,4 | 1,0 | 2,2 | 11,2 | 31,0 | 2,8 | 3,5 | 2,2 | |||||||||
| 21,0 | 6,0 | 4,8 | 1,4 | 3,6 | 15,0 | 37,5 | 2,5 | 3,0 | 1,8 | |||||||||
| 32,5 | 10,0 | 5,4 | 2,5 | 4,0 | 48,0 | 12,0 | 3,0 | 3,6 | 2,4 | |||||||||
| 15,0 | 17,0 | 1,0 | 2,0 | 2,5 | 38,4 | 13,4 | 3,2 | 3,5 | 2,5 | |||||||||
| 6,0 | 12,0 | 1,2 | 2,5 | 3,0 | 29,4 | 10,2 | 2,1 | 2,8 | 1,6 | |||||||||
| 11,9 | 16,1 | 2,8 | 3,0 | 24,8 | 8,7 | 1,8 | 2,5 | 1,2 | ||||||||||
| 6,4 | 17,6 | 1,6 | 3,0 | 3,2 | 39,0 | 5,4 | 2,6 | 3,2 | 2,1 | |||||||||
| 10,8 | 16,4 | 1,8 | 3,2 | 3,5 | 42,5 | 12,6 | 3,4 | 4,0 | 2,3 | |||||||||
Алгоритм решения
1. Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, и места изменения размеров поперечного сечения.
2. Определить по методу сечения продольную силу для каждого участка, построить эпюру продольных сил. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.
3. Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.
4. Перемещение свободного конца определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука
Пример выполнения
Задача
Построить эпюры: продольных сил, нормальных напряжений и перемещений. Определить абсолютное удлинение (укорочение). Модуль упругости принять 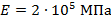

Решение
1. За начало отсчета принимаем свободный конец
2. Разбиваем брус на характерные участки, в зависимости от точки приложения силы и изменения поперечного сечения.
Имеем четыре участка
3. Каждый участок разбиваем на сечения. В сечении возникает продольная сила 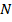 . В пределах участка – const. Знаки: растяжение-плюс; сжатие- минус. В общем случае
. В пределах участка – const. Знаки: растяжение-плюс; сжатие- минус. В общем случае  .
.
И так:
| сеч I-I |  - на участке -const - на участке -const |
| сеч II-II | 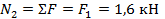 |
| сеч III-III |  |
| сеч IV-IV | 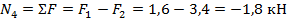 |
4. На основании данных строим эпюру продольных сил в масштабе
1 см – 0,4 кН.

5. Нормальные напряжения определяем
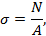
где 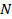 – продольная сила на участке, берется из эпюры, Н
– продольная сила на участке, берется из эпюры, Н
 - площадь поперечного сечения на участке,
- площадь поперечного сечения на участке, 
И так
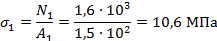
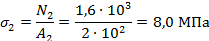
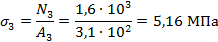

Строим эпюру эпюру нормальных напряжений в масштабе
1 см- 2 МПа. Из эпюры видно, что
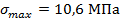 - опасное сечение (участок I-I)
- опасное сечение (участок I-I)
6. Определить абсолютное удлинение (укорочение)


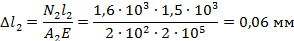
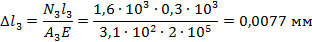
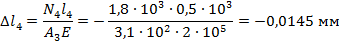
И так
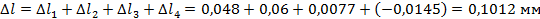
Брус удлинился на 0,1012 мм.
7. Перемещение составляет алгебраическую сумму перемещений от действия каждой силы в отдельности
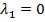
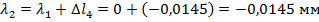
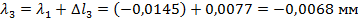


Контрольные вопросы.
1. Как нужно нагрузить прямой брус, чтобы он работал только на растяжение (сжатие)?
2. Что такое продольная и поперечная деформация бруса и какова зависимость между ними?
3. Сформулируйте закон Гука. Каков физический смысл модуля продольной упругости Е?
4. Как определяется удлинение (укорочение) участка бруса с постоянным поперечным сечением и постоянной продольной силой по всей его длине?
5. Влияет ли форма поперечного сечения на величину напряжений, возникающих при растяжении, сжатии?
6. Что называется эпюрой и для чего они строятся?
7. Каков закон изменения нормальных напряжений по площади поперечного сечения при растяжении, сжатии?
СР №12
