Наличие нейтрального элемента

Примерный перечень ответов к зачету

по темам «Графы и их приложения» и «Алгебраические структуры»

Графы и их приложения

1. Неориентированный граф – это граф, рёбрам которого не присвоено направление.

Псевдограф – граф, у которого могут быть кратные ребра и/или петли.

Мультиграф – граф, у которого могут быть кратные ребра, но нет петлей.

Графы помогают описывать и исследовать различные системы объектов и их связи.

2. Ориентированный граф – это граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами и просто рёбрами.

Псевдограф – граф, у которого могут быть кратные ребра и/или петли.

Мультиграф – граф, у которого могут быть кратные ребра, но нет петлей.

Графы помогают описывать и исследовать различные системы объектов и их связи.

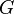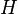3. Графы и являются изоморфными, если путем перестановки строк и столбцов матрицы смежности графа 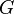удается получить матрицу смежности графа .

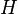Графы G1 и G2 наз. гомеоморфными, если существуют такие их подразбиения, к-рые изоморфны.

Двудольный граф — это граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.

Двудольный граф называется полным, если для каждой пары вершин 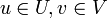существует ребро 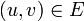. Для

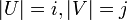
такой граф называется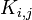

4. Маршрут – это путь между вершинами графа, проходящий вдоль ребер.

Путь — это последовательность вершин таких, что две любые последовательные вершины соединены хотя бы одной дугой.

Точка сочленения графа — вершина графа, при удалении которой граф имеет больше компонент связности, чем исходный граф.

Мост — это ребро, удаление которого увеличивает количество компонент связности.

Блок графа - это связный подграф, который не имеет точек сочленения.

5. Определение. Матрицей смежности орграфа D называется квадратная матрица A(D)=[aij] порядка n, у которой

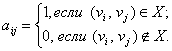
Определение. Матрицей инцидентности орграфа D называется (nґm) –матрица B(D)=[bij], у которой

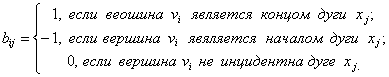
Введем также матрицы смежности и инцидентности для неориентированных графов. Пусть G = (V, X) – граф, где V={v1, v2, …,vn}, X={x1, x2, …, xm}.

Определение. Матрицей смежности графа G называется квадратная матрица A(G)=[aij] порядка n, у которой

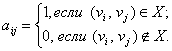
Определение. Матрицей инцидентности графа G называется (nґm) –матрица B(G)=[bij], у которой

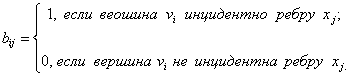
6. Объединением графов 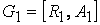и 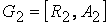называется граф 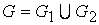, множество вершин которого есть объединение множеств вершин графов 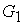и 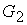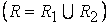, а множество ребер является объединением множеств ребер этих графов .

Пересечением графов 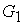и 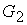называется граф 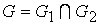, множество вершин которого 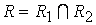, а множество ребер .

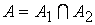Подграф – это часть графа.

7. Граф G называется связным, если для любой пары различных вершин этого графа существует цепь, соединяющая эти вершины.

Если для графа G можно указать пару различных вершин, которые не соединяются цепью (простой цепью), то граф называется несвязным.

Компонента связности графа — некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.

Матрицей связности S графа называется квадратная симметричная матрица размера n 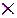n, в которой каждый элемент S 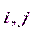= 1, если j-а вершина достижима из i-й вершины, и S 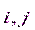=0 в противном случае.

8. Маршрут в графе – чередующаяся последовательность вершин и ребер.

9. Дерево — это связный ациклический граф.^[1] Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.

- Дерево не имеет кратных рёбер и петель.

- Любое дерево с 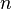вершинами содержит 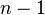ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда 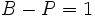, где 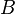— число вершин, 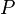— число рёбер графа.

- Граф является деревом тогда и только тогда, когда любые две различные его вершины можно соединить единственной простой цепью.

- Любое дерево однозначно определяется расстояниями (длиной наименьшей цепи) между его концевыми (степени 1) вершинами.

- Любое дерево является двудольным графом. Любое дерево, множество вершин которого не более чем счётное, является планарным графом.

- Для любых трёх вершин дерева, пути между парами этих вершин имеют ровно одну общую вершину.

Лес — граф, не содержащий циклов

10. Остовное дерево — ациклический связный подграф данного связного неориентированного графа, в который входят все его вершины.

Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.

11. Нагруженный граф − ориентированный граф D=(V,X), на множестве дуг которого определена некоторая функция 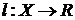, которую называют весовой функцией.

Цифра над дугой (см. рис. 5)− вес дуги (цена дуги).

Путь в нагруженном ориентированном графе из вершины v в вершину w, где v¹w, называется минимальным, если он имеет наименьшую длину

12. Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. (ср. Гамильтонов путь)

Эйлеров цикл — это эйлеров путь, являющийся циклом.

Эйлеров граф — граф, содержащий эйлеров цикл.

13. Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл.

Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз.

14. Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.

Плоский граф — граф, уложенный на плоскость.

15. Правильная раскраска графа — раскраска, при которой каждый цветной класс является независимым множеством. Иначе говоря, в правильной раскраске любые две смежные вершины должны иметь разные цвета.

16. Раскраска графа — разбиение вершин на множества (называемые цветами). Если при этом нет двух смежных вершин принадлежащих одному и тому же множеству (то есть две смежные вершины всегда разного цвета), то такая раскраска называется правильной.

17. Сеть — в принципе, то же, что и граф, хотя сетями обычно называют графы, вершины которых определённым образом помечены.

· Ориентированная сеть — ориентированный граф, не содержащий контуров.

Алгебраические структуры

Бинарные операции

Ниже перечислены основные операции над множествами:

· пересечение:

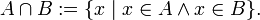
· объединение:

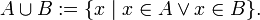
Если множества 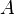и 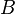не пересекаются,то 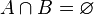. Их объединение обозначают также: .

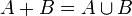· разность (дополнение):

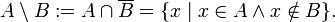
· симметрическая разность:

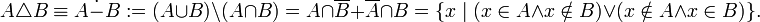
· Декартово или прямое произведение:

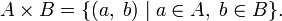
2. Алгебраическая система (или алгебраическая структура) в универсальной алгебре — множество 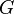(носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системеаксиом.

3. Гру́ппа — непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам.

4. Свойства групп:

Ассоциативность

наличие нейтрального элемента