Случайные величины. закон нормального распределения случайных величин

Многие случайные события могут быть оценены количественно случайными величинами. Случайной величиной называется величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Полными, исчерпывающими характеристиками случайных величин являются так называемые законы распределения. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Цель занятия:

1. Изучить законы распределения и методы вычисления числовых характеристик случайных величин.

2. Изучить нормальный закон распределения случайных величин и метод вычисления вероятности при нормальном распределении.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Величина, принимающая те или иные числовые значения в зависимости от различных случайных обстоятельств, называется случайной величиной. Случайными величинами являются: число больных на приеме у врача, число студентов в аудитории, число рождений в городе, продолжительность жизни отдельного человека, температура воздуха и др.

Различают дискретные и непрерывные случайные величины. Случайная величина, принимающая отдельные, изолированные числовые значения, называется дискретнойили прерывной (например, число студентов на лекции, число случаев заболеваний, число родившихся за один день мальчиков и др.).

Случайная величина, принимающая любые значения в определенном интервале, называется непрерывной(например, температура тела больного, продолжительность жизни человека, температура воздуха в течение дня и т.д.).

1. ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Случайные величины обозначают прописными буквами латинского алфавита: X, Y, Z,…, а их возможные значения – соответствующими строчными буквами x, y, z... .

Рассмотрим дискретную случайную величину X с возможными значениями x₁, x₂,…, x_n. Величина Xможет принять каждое из них с некоторой вероятностью. В результате испытания величина X примет одно из этих значений, т.е. произойдет одно из полной группы несовместных событий. Обозначим вероятности этих событий буквами P с соответствующими индексами: P(X=x₁)=P₁, P(X=x₂)=P₂,…,P(X=x_n)=P_n.

Так как все возможные значения дискретной случайной величины представляют полную группу, то сумма вероятностей равна единице:

P₁+P₂+…+P_n= 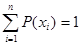- условие нормировки.

Дискретная случайная величина X считается заданной, если перечислены все ее возможные значения и вероятности, с которыми она может принимать эти значения.

Законом распределения дискретной случайной величины называется соответствие между ее возможными значениями и их вероятностями.

Закон распределения дискретной случайной величины может быть представлен в виде таблицы, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:

Значения случайной величины, xi	x1	x2	…	xn
Вероятности, Pi	P1	P2	…	Pn

Такую таблицу называют рядом распределения случайной величины X.

Ряд распределения можно представить графически: по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений, и для наглядности полученные точки соединяются отрезками прямых (рис. 1). Такая фигура называется многоугольником распределения. Многоугольник распределения полностью характеризует случайную величину и является одной из форм закона распределения.

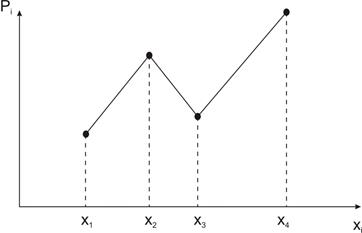
Рис 1. Многоугольник распределения.