Характеристики якості вимірювань. похибки вимірювань

Теоретичні відомості

На практиці для кількісного оцінювання якості вимірювання найчастіше застосовують негативну характеристику - похибку результату вимірювання або часто просто похибку вимірювання як відхилення результату вимірювання 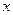від істинного (справжнього) значення 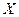вимірюваної величини.

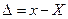(3.1)

Застосуванню похибки для оцінювання якості вимірювань сприяє те, що похибки ЗВТ можна визначити (принаймні наближено) експериментально, наприклад, подаючи на їх вхід відоме значення величини і зіставляючи з ним отриманий результат. Експериментально можна перевірити методики вимірювань тих чи інших величин, що виконуються певними ЗВТ в певних умовах.

Похибки вимірювань виникають внаслідок різноманітних причин (див. наступні розділи), зокрема від неадекватної моделі вимірювальної величини, неідеальності властивостей ЗВТ, небажаної їх взаємодії з об'єктом вимірювання, впливу інших фізичних об'єктів тощо. Завдяки глибокому вивченню об'єкта і вимірювальної величини, покращанню засобів вимірювальної техніки, способів їх використання, методик виконання вимірювань, корекції та опрацювання результатів тощо, вплив похибок на результат вимірювання зменшують, а значить, зменшують похибку вимірювання.

Однак принципово зазначені фактори не можна усунути чи виключити повністю. Тому у наведеному рівнянні похибки залишаються дві невідомі величини — істинне значення вимірюваної величини і похибка і за відомого результату вимірювання неможливо встановити ні Істинне значення величини, ні фактичне значення похибки.

Якщо б похибку можна було знайти точно, то відразу можна було би випра­вити результат вимірювання і отримати істинне значення величини, тобто похибка перестала би бути похибкою. Оскільки неможливо точно визначити похибку вимірювання, то неможливе і абсолютно точне вимірювання, що є одним з головних протиріч вимірювань.

На практиці, щоб вирішити це протиріччя, визначають не точне значення похибки вимірювання, а оцінюють певні її характеристики, зокрема деякий інтервал, в якому вона може знаходитися. Цей інтервал може бути з твердими (безумовними) границями в тому значенні, що ні за яких умов похибка вимірювання не вийде з цього інтервалу або з м’якими чиумовними (імовірнісними, довірчими чи вірогідними) границями, в тому значенні, що похибка вимірювання знаходиться в цьому інтервалі лише з певною ймовірністю.

Кінцевою метою аналізу похибок вимірювань якраз є оцінювання границь (умовних чи безумовних), в яких міститься фактичне значення похибки. Вважають, що результат вимірювання разом з інтервалом, що визначається границями похибки вимірювання, накриває з певною ймовірністю істинне значення вимірюваної величини.

Абсолютна похибка.Наведене вище означення похибки є власне означенням абсолютної похибки. Термін „абсолютна похибка” не означає абсолютного значення чи модуля похибки 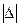. Важливим також є те, що на першому місці у (3.1) стоїть виміряне значення 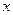, а на другому — справжнє (істинне) значення 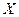, а не навпаки.

Одиницею абсолютної похибки є одиниця вимірюваної величини. Тобто якщо вимірюють електричну напругу, то абсолютна похибка буде мати розмірність напруги (вольт (В), мілівольт (мВ), мікровольт (мкВ), нановольт (нВ) кіловольт (кВ) тощо).

Така домовленість у послідовності величин в означенні похибки потрібна для правильного коригування систематичних похибок, зокрема, введенням відповідних поправок до результату вимірювань. Коли говорять просто „похибка вимірювання”, то переважно мають на увазі абсолютну похибку.

Відносна похибка. Для порівняння якості вимірювань різних значень однієї величини або різних вимірюваних величин абсолютна похибка є незручною. Для кількісної характеристики якості вимірювання у таких випадках використовують відносну похибку, теоретично як відношення абсолютної похибки до істинного (справжнього) значення вимірюваної величини, а практично — до виміряного значення (результату) (найчастіше виражене у відсотках)

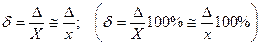(3.2)

Чим менша відносна похибка, тим точніше вимірювання і навпаки.

Відмінність між теоретичним ( 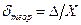) та практичним ( 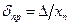) значеннями відносної похибки дуже мала (має другий порядок малості).

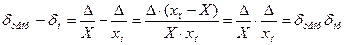(3.3)

звідки 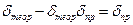і далі 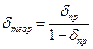різниця між ними -

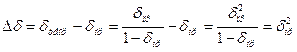(3.4)

Зокрема, навіть при відносній похибці 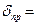5% = 0,05 теоретичне значення похибки буде відрізнятися від практичного (похибка від похибки) не більше ніж на

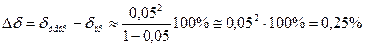
Тому на практиці такою різницею нехтують.

Відносну похибку можуть також залишати безрозмірною (у відносних одиницях) чи, якщо похибка набуває дуже малі значення - у мільйонних частках ррт: .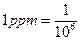

Загалом 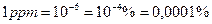; 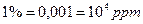(3.5)

Задача 12.Виконано три вимірювання. У першому випадку вимірювали товщину сталевої пластини і отримали значення 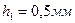з похибкою 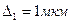, у другому — висоту кімнати 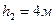з похибкою 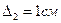, у третьому-відстань між містами 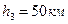з похибкою 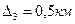. Встановити, в якому випадку точність вимірювання вища.

Розв’язання. 1. За абсолютними похибками відразу важкосказати, в якому випадку точність вимірювання була вища. Для цього знайдемо відносні похибки. Для вказаних результатів та їх абсолютних похибок відносні похибки становлять:

товщини пластини —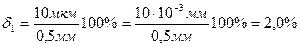
висоти кімнати —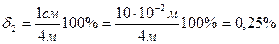
відстані між містами —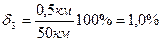

2. Як бачимо, висота кімнати виміряна з найвищого точністю (відносна похибка 0,25 %), атовщина пластини — з найменшою (відносна похибка — 2,0 %).

Задача 13.Виміряли температуру 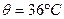з похибкою 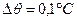, і напругу в мережі 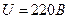з похибкою 1 В. Встановити, в якому випадку точність вимірювання краща.

Розв’язашія. 1. При вимірюванні температури відносна похибка

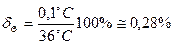
2. Під час вимірювання напруги

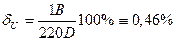
3. Отже, точніше виміряли температуру, оскільки тут відносна похибка є меншою.

Задача 14.Відносне значення похибки 0,0005 подати у відсотках та ррт.

Розв’язания, 1. Значення похибки у відсотках

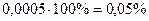
2.Значення похибки у ррm

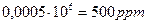
3.Загалом

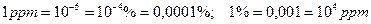
Задача 15.Нехай електричний чотириполюсник описується системою рівнянь

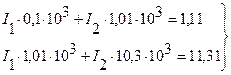
Відомо, що 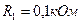, , 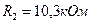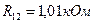. Виміряли напруги 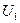та 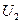, і отримали значенням 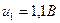та .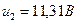

А. За цими результатами вимірювань необхідно знайти значення струмів 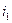та .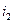

Розв'язання 1. Підставимо одержані значення у систему рівнянь, що описує чотириполюсник

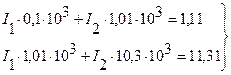
розв’язавши яку, отримуємо

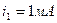та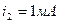

Б. Нехай під час вимірювання напруги допущені похибки орієнтовно 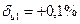, тобто 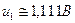, а 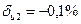, тобто 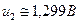. Оцінити струми чотириполюсника.

2. Підставивши ці значення у задану систему рівнянь

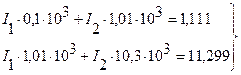
після розв’язування одержимо

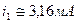та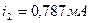

Як бачимо, достатньо малі похибки вимірювань напруги (± 0,1 %) призвели до дуже великої зміни результатів розрахунку: збільшення першого струму на 216 %, і зменшення другого на 21 %.

Задача 16.Нехай загальний опір електричного кола становить 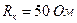, а опір амперметра 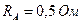. Показ амперметра 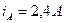. Оцінити відносну та абсолютну методичні похибки вимірювання струму, спричинені увімкненням у коло амперметра з ненульовим опором.

Роїв’язання. 1. Використовуючи вираз (6,6), обчислимо відносну методичну похибку вимірювання струму

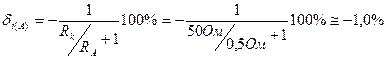
2. Застосовуючи вираз (6.7), знайдемо абсолютну методичну похибку вимірювання струму

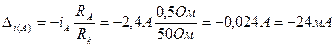
Практичне заняття №4