Характеристика закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли
Дисперсия непрерывной случайной величины. Стандартное отклонение.
Дисперсией случайной величины Х называется Математическое ожидание Е (Х — mх)2 квадрата отклонения Х от её математического ожидания mх = Е (Х). Д. случайной величины Х обозначается через D (X) или через σ2X. Квадратный корень из Д. (т. е. σ, если Д. есть σ2) называется средним квадратичным отклонениемДля непрерывной случайной величины x, заданной плотностью распределения :
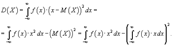
Дисперсия и квадратный корень из дисперсии, называемый стандартным отклонением, характеризуют среднее отклонение от среднегозначения выборки. Среди этих двух величин наиболее важное значение имеет стандарт отклонение. Это значение можно представитькак среднее расстояние, на котором находятся элементы от среднего элемента выборки.
 Стандартное отклонение вы числяется путем определения сначала дисперсии и затем вычисления квадратного корня из дисперсии.
Стандартное отклонение вы числяется путем определения сначала дисперсии и затем вычисления квадратного корня из дисперсии.
Понятие и примеры системы случайных величин.
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
Примеры случайных величин:
1) число попаданий при трех выстрелах;
2) число вызовов, поступавших на телефонную станцию за сутки;
3) частота попадания при 10 выстрелах.
Характеристика закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли
если влияние на сумму отдельных слагаемых является равномерно малым, закон распределения суммы приближается к нормальному. Математическая формулировка этого утверждения дается в группе теорем,называемой законом больших чисел.
Теорема (неравенство Чебышева).p( | X – M(X)| < ε ) ≥ D(X) / ε2.
Теорема 13.2 (теорема Чебышева). Если Х1, Х2,..., Хп – попарно независимые случайные величины, дисперсии которых равномерно ограничены ( D(Xi) ≤ C), то для сколь угодно малого числа ε вероятность неравенства
Х1 +Х2 +...+Хп −М(Х1)+М(Х2)+...+М(Хп) <ε будет сколь угодно близка к 1, если число случайных величин достаточно велико. Замечание. Иначе говоря, при выполнении этих условий
limp(Х1 +Х2 +...+Хп −М(Х1)+М(Х2)+...+М(Хп) <ε)=1.
Теорема (Бернулли). Если в каждом из п независимых опытов вероятность р появления события А постоянна, то при достаточно большом числе испытаний вероят- ность того, что модуль отклонения относительной частоты появлений А в п опытах от р будет сколь угодно малым, как угодно близка к 1 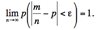

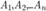 равна сумме вероятностей этих событий
равна сумме вероятностей этих событий 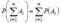 Доказательство. Докажем эту теорему для случая суммы двух несовместных событий
Доказательство. Докажем эту теорему для случая суммы двух несовместных событий 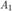 и
и 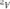 . Пусть событию
. Пусть событию 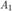 благоприятствуют
благоприятствуют 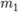 элементарных исходов, а событию
элементарных исходов, а событию 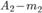 исходов. Так как события
исходов. Так как события 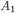 и
и 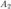 по условию теоремы несовместны, то событию
по условию теоремы несовместны, то событию 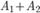 благоприятствуют
благоприятствуют 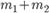 элементарных исходов из общего числа n исходов. Следовательно,
элементарных исходов из общего числа n исходов. Следовательно, 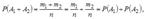 , где
, где 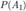 — вероятность события A;
— вероятность события A; 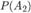 — вероятность события
— вероятность события  . 10. Теорема сложения вероятностей для совместных событий. Теорема: Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного появления, т.е. Р(А+В)=Р(А)+Р(В)-Р(АВ). Доказательство: Всего исходов N, благоприятствующ событию А- К, событию В- L, совместному появлению А и В- М. Следовательно, благоприятных исходов для события А+В : K+L-M. Откуда вероятность события А+В:
. 10. Теорема сложения вероятностей для совместных событий. Теорема: Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного появления, т.е. Р(А+В)=Р(А)+Р(В)-Р(АВ). Доказательство: Всего исходов N, благоприятствующ событию А- К, событию В- L, совместному появлению А и В- М. Следовательно, благоприятных исходов для события А+В : K+L-M. Откуда вероятность события А+В: 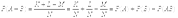 12. Ф-а полной вероятности и формулы Байеса. Предположим, что событие B может осуществляться только с одним из несовместных событий
12. Ф-а полной вероятности и формулы Байеса. Предположим, что событие B может осуществляться только с одним из несовместных событий 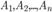 . Например, в магазин поступает одна и та же продукция от трех предприятий в разном количестве. Существует разная вероятность выпуска некачественной продукции на разных предприятиях. Случайным образом отбирается одно из изделий. Требуется определить вероятность того, что это изделие некачественное (событие B). Здесь событияA1,,A2,A3 — это выбор изделия из продукции соответствующего предприятия. В этом случае вероятность события B можно рассматривать как сумму произведений событий
. Например, в магазин поступает одна и та же продукция от трех предприятий в разном количестве. Существует разная вероятность выпуска некачественной продукции на разных предприятиях. Случайным образом отбирается одно из изделий. Требуется определить вероятность того, что это изделие некачественное (событие B). Здесь событияA1,,A2,A3 — это выбор изделия из продукции соответствующего предприятия. В этом случае вероятность события B можно рассматривать как сумму произведений событий 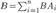 По теореме сложения вероятностей несовместных событий получаем
По теореме сложения вероятностей несовместных событий получаем 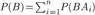 Используя теорему умножения вероятностей, находим
Используя теорему умножения вероятностей, находим 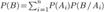 Формула носит название формулы полной вероятности. Формула Байеса Пусть событие B происходит одновременно с одним из n несовместных событий
Формула носит название формулы полной вероятности. Формула Байеса Пусть событие B происходит одновременно с одним из n несовместных событий 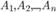 . Требуется найти вероятность события
. Требуется найти вероятность события 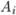 , если известно, что событие B произошло. На основании теоремы о вероятности произведения двух событий можно написать
, если известно, что событие B произошло. На основании теоремы о вероятности произведения двух событий можно написать  Откуда
Откуда 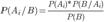 или
или 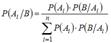 Формула носит название формулы Байеса. 16 Теорема Пуассона: формулировка теоремы, приближенная формула. Теорема Пуассона в теории вероятностей описывает способ получения распределения Пуассона как предел биномиальных распределений. Формулировка Пусть есть
Формула носит название формулы Байеса. 16 Теорема Пуассона: формулировка теоремы, приближенная формула. Теорема Пуассона в теории вероятностей описывает способ получения распределения Пуассона как предел биномиальных распределений. Формулировка Пусть есть 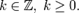 Пусть также дана последовательность
Пусть также дана последовательность 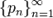 такая, что
такая, что 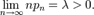 Тогда
Тогда 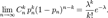 Уточнённая теорема Пуассона Пусть
Уточнённая теорема Пуассона Пусть 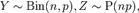 и
и 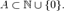 Тогда
Тогда 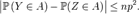 17. Наивероятнейшее число появления события A в n испытаниях. Число m0 называется наивероятнейшим числом наступлений события А в n испытаниях и равно целой части числа (n+1)p, а при целом (n+1)p наибольшее значение достигается при двух числах: m1=(n+1)p-1 и m2=(n+1)p. Если р≠0 и р≠1, то число m0 можно определить из двойного неравенства np-q ≤ m0 ≤ np+p. 28. Непрерывные случайные величины. Плотность распределения вероятностей непрерывной случайной величины, или дифференциальная функция распределения, ее вероятностный смысл и основные св-ва. Функцией распределения вероятностей называют функцию F(X), определяющую вероятность того, что случайная величина x в результате испытания примет значение, меньшее x, то есть: F(X)=P(X<x)
.
Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. Плотностью распределения вероятностей непрерывной случайной величины x называют функцию f(x) – первую производную от функции распределения вероятностей F(X):
f(x)=F’(x).
Таким образом, функция распределения вероятностей является первообразной для плотности распределения вероятностей.
17. Наивероятнейшее число появления события A в n испытаниях. Число m0 называется наивероятнейшим числом наступлений события А в n испытаниях и равно целой части числа (n+1)p, а при целом (n+1)p наибольшее значение достигается при двух числах: m1=(n+1)p-1 и m2=(n+1)p. Если р≠0 и р≠1, то число m0 можно определить из двойного неравенства np-q ≤ m0 ≤ np+p. 28. Непрерывные случайные величины. Плотность распределения вероятностей непрерывной случайной величины, или дифференциальная функция распределения, ее вероятностный смысл и основные св-ва. Функцией распределения вероятностей называют функцию F(X), определяющую вероятность того, что случайная величина x в результате испытания примет значение, меньшее x, то есть: F(X)=P(X<x)
.
Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. Плотностью распределения вероятностей непрерывной случайной величины x называют функцию f(x) – первую производную от функции распределения вероятностей F(X):
f(x)=F’(x).
Таким образом, функция распределения вероятностей является первообразной для плотности распределения вероятностей.  Свойства плотности распределения вероятностей 1. Плотность распределения вероятностей – неотрицательная функция:
f(x)=>0 .
2.Несобственный интеграл от плотности распределения вероятностей в пределах от
Свойства плотности распределения вероятностей 1. Плотность распределения вероятностей – неотрицательная функция:
f(x)=>0 .
2.Несобственный интеграл от плотности распределения вероятностей в пределах от  до
до 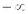 равен единице:
равен единице:
 .Вероятностный смысл плотности распределения вероятности. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу
.Вероятностный смысл плотности распределения вероятности. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу 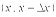 , приближенно равна (с точностью до бесконечно малых высшего порядка относительно
, приближенно равна (с точностью до бесконечно малых высшего порядка относительно 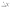 ) произведению плотности распределения вероятности в точке на длину интервала
) произведению плотности распределения вероятности в точке на длину интервала 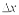 :
:
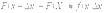 . 32. Нормальное распределение непрерывной случайной величины и его параметры. Плотность вероятности нормированного нормального распределения таблица значений этой функции. Нормальным называют распределение вероятностей непрерывной случайной величины, которое задается плотностью
. 32. Нормальное распределение непрерывной случайной величины и его параметры. Плотность вероятности нормированного нормального распределения таблица значений этой функции. Нормальным называют распределение вероятностей непрерывной случайной величины, которое задается плотностью
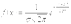 .
Нормальное распределение задается двумя параметрами: a – математическим ожиданием,
.
Нормальное распределение задается двумя параметрами: a – математическим ожиданием,  – средним квадратическим отклонением.
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
Нормированным называют нормальное распределение с параметрами
– средним квадратическим отклонением.
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
Нормированным называют нормальное распределение с параметрами 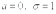 .
Плотность нормированного распределения задается формулой
.
Плотность нормированного распределения задается формулой
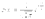 .
. Случайная величина x нормально распределена с параметрами a и s , s >0, если ее плотность распределения px(x ) и функция распределения Fx(x) имеют соответственно вид: 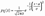 , , 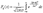 , Mx = a, Dx = s2. Часто используемая запись x ~ N(a, s ) означает, что случайная величина x имеет нормальное распределение с параметрами a и s . Говорят, что случайная величина x имеет стандартное нормальное распределение, если a = 0 и s = 1 (x ~ N(0, 1)). Плотность и функция распределения стандартного нормального распределения имеют вид: , Mx = a, Dx = s2. Часто используемая запись x ~ N(a, s ) означает, что случайная величина x имеет нормальное распределение с параметрами a и s . Говорят, что случайная величина x имеет стандартное нормальное распределение, если a = 0 и s = 1 (x ~ N(0, 1)). Плотность и функция распределения стандартного нормального распределения имеют вид: 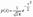 , , 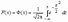 , Mx= 0, Dx= 1. Здесь , Mx= 0, Dx= 1. Здесь 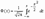 - функция Лапласа. Функция распределения нормальной величины x ~ N(a, s ) выражается через функцию Лапласа следующим образом: - функция Лапласа. Функция распределения нормальной величины x ~ N(a, s ) выражается через функцию Лапласа следующим образом: 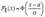 . Если x ~ N(a, s ), то случайную величину h = (x-a)/s называют стандартизованной или нормированной случайной величиной; h ~ N(0, 1) - имеет стандартное нормальное распределение. Таблица значений плотности ста ндартного нормальног о распределения. . Если x ~ N(a, s ), то случайную величину h = (x-a)/s называют стандартизованной или нормированной случайной величиной; h ~ N(0, 1) - имеет стандартное нормальное распределение. Таблица значений плотности ста ндартного нормальног о распределения. 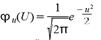 |
37. Понятие функции одного случайного аргумента. Нахождение распределения функции по известному распределению дискретного и непрерывного аргумента.Если каждому возможному значению случайной величины X соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента X: Y = φ (X).
