Глава 2. Дифференцирование функций. 224. 225. 1) y = u3, u = sin v, v = 2x +1; 2) y = eu, u = arctg v, , z = 1 + t, t = ln s, s = 2x +3; 3) y = sin v
224. 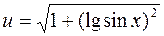 . 225. 1) y = u3, u = sin v, v = 2x +1; 2) y = eu, u = arctg v,
. 225. 1) y = u3, u = sin v, v = 2x +1; 2) y = eu, u = arctg v, 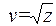 , z = 1 + t, t = ln s, s = 2x +3; 3) y = sin v, v = ln u, u = arcctg z, z = 2x. 227. x1 = 0, x2 = 4. 228. x1 = -2, x2 = 5, x3 =
, z = 1 + t, t = ln s, s = 2x +3; 3) y = sin v, v = ln u, u = arcctg z, z = 2x. 227. x1 = 0, x2 = 4. 228. x1 = -2, x2 = 5, x3 = 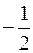 .
.
229. 1) не определена только при x = 0, x = -1, x = 1; 2) 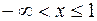 и
и 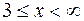 , в интервале (1;3) функция не определена; 3)
, в интервале (1;3) функция не определена; 3) 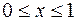 ; 4)
; 4) 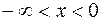 ; 5) не имеет смысла. 230. 1) да; 2) тождественны на интервале (0; ¥). 231. 1), 2), 8) – четные; 3), 5), 6), 9) — нечетные; 4), 7) — ни четные, ни нечетные.
; 5) не имеет смысла. 230. 1) да; 2) тождественны на интервале (0; ¥). 231. 1), 2), 8) – четные; 3), 5), 6), 9) — нечетные; 4), 7) — ни четные, ни нечетные.
232. 1) 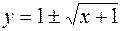 ; 2)
; 2) 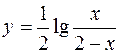 ; 3)
; 3) 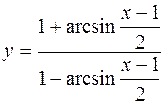 . 233. v = sin (1 + x). 234. 1) y = 5u, u = v2, v = 3x +1; 2) y = ln z, z = cos u, u = arctg v,
. 233. v = sin (1 + x). 234. 1) y = 5u, u = v2, v = 3x +1; 2) y = ln z, z = cos u, u = arctg v, 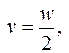 w = t – s, t = ex, s = eq, q = –x; 3) y = arcos u, u = ln v, v = tg z, z = 4x. 237. 4 и -2; -2, 2, 4, 10. 238.1) вся числовая ось, кроме точек x = 1 и х = 2; 2)
w = t – s, t = ex, s = eq, q = –x; 3) y = arcos u, u = ln v, v = tg z, z = 4x. 237. 4 и -2; -2, 2, 4, 10. 238.1) вся числовая ось, кроме точек x = 1 и х = 2; 2) 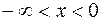 и
и 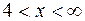 ; 3)
; 3) 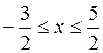 ; 4)
; 4) 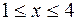 . 239. 1) тождественны на любом интервале, не содержащем точку х = 0; 2) тождественны на промежутке [0; ¥). 240. 4), 5), 6) — четные; 3), 7) — нечетные; 1), 2), 8) — ни четные, ни нечетные. 241. 1)
. 239. 1) тождественны на любом интервале, не содержащем точку х = 0; 2) тождественны на промежутке [0; ¥). 240. 4), 5), 6) — четные; 3), 7) — нечетные; 1), 2), 8) — ни четные, ни нечетные. 241. 1) 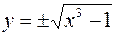 ; 2)
; 2) 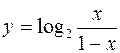 ; 3)
; 3) 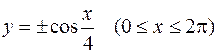 . 242.
. 242. 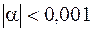 , как только
, как только 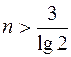 или
или 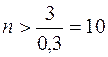 ;
; 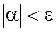 , как только
, как только 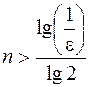 .
.
243. 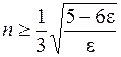 , если
, если 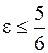 ; n = 0, если
; n = 0, если 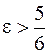 . 244.
. 244. 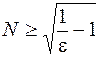 , если
, если 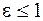 ; N = 0, если e > 1. 245. При
; N = 0, если e > 1. 245. При 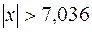 . 246.
. 246. 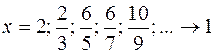 ;
; 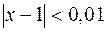 , как только
, как только 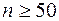 ;
; 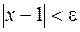 , как только
, как только 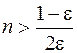 . 247. N = 19999. 248.
. 247. N = 19999. 248. 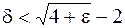 ; d < 0,00025.
; d < 0,00025.
249. При 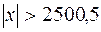 . 250. 0,5. 251. ¥. 252. 0. 253. 1. 254. 4. 255. 0.
. 250. 0,5. 251. ¥. 252. 0. 253. 1. 254. 4. 255. 0.
256.  . 257. 0. 258. –2. 259.
. 257. 0. 258. –2. 259. 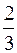 . 260. 2,5. 261. –¥. 262. –1. 263. 0,25. 264. 0. 265. 100. 266. 1. 267.
. 260. 2,5. 261. –¥. 262. –1. 263. 0,25. 264. 0. 265. 100. 266. 1. 267. 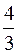 . 268. –0,5. 269. 0. 270. 0.
. 268. –0,5. 269. 0. 270. 0.
271. 1. 272. 3. 273. 0. 274. 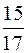 . 275. 0. 276.
. 275. 0. 276. 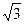 . 277. –1,5. 278. 1.
. 277. –1,5. 278. 1.
279. –2,5. 280. 0. 281. ¥. 282. 0,5. 283. 0. 284. –1. 285. –0,5. 286. ¥.
287. 0,5. 288. –1. 289. 0. 290. 1. 291. 9. 292. -0,6. 293.1,5. 294. 1.
295. ¥. 296. 0,25. 297. 4. 298. 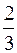 . 299. 0,5. 300.
. 299. 0,5. 300. 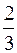 . 301. 0,4. 302. 0,75.
. 301. 0,4. 302. 0,75.
303. 1. 304. 6. 305. 0,5. 306. 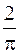 . 307. –0,5. 308. 0,125. 309. 0. 310. –1.
. 307. –0,5. 308. 0,125. 309. 0. 310. –1.
311. 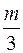 . 312.
. 312. 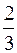 . 313.
. 313. 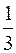 . 314. –0,25. 315. 3. 316. ¥. 317. 1. 318. –1.
. 314. –0,25. 315. 3. 316. ¥. 317. 1. 318. –1.
319. 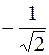 . 320. 2. 321. 3. 322. -2. 323. 0,5. 324. e-4. 325. 1. 326.
. 320. 2. 321. 3. 322. -2. 323. 0,5. 324. e-4. 325. 1. 326. 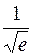 .
.
327. Функция непрерывна в области [-8; -1), (-1; 1), (1; +¥); при х = 1 устранимый разрыв (положить 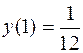 ), при х = -1 разрыв второго рода:
), при х = -1 разрыв второго рода: 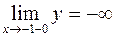 ,
, 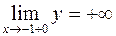 . 328. Функция непрерывна в области (-¥; -1), (-1; 1), (1; 15]; при х = -1 устранимый разрыв (положить
. 328. Функция непрерывна в области (-¥; -1), (-1; 1), (1; 15]; при х = -1 устранимый разрыв (положить
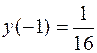 ), при х = 1 разрыв второго рода:
), при х = 1 разрыв второго рода: 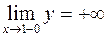 ,
, 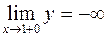 .
.
329. e-2. 330. 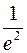 . 331.
. 331. 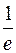 . 332. Функция непрерывна в области (-¥; -2), (-2; 2), (2; 11]; при х = 2 устранимый разрыв (положить
. 332. Функция непрерывна в области (-¥; -2), (-2; 2), (2; 11]; при х = 2 устранимый разрыв (положить 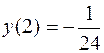 ), при х = -2 разрыв второго рода:
), при х = -2 разрыв второго рода: 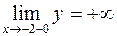 ,
, 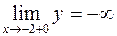 . 333. Функция непрерывна в области (-¥; -1), (-1; 1), (1; 3]; при х = -1 устранимый разрыв (положить
. 333. Функция непрерывна в области (-¥; -1), (-1; 1), (1; 3]; при х = -1 устранимый разрыв (положить 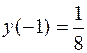 ), при х = 1 разрыв второго рода:
), при х = 1 разрыв второго рода: 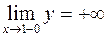 ,
, 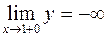 .
.
334. 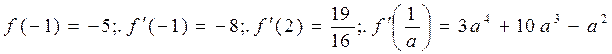 .
.
335. 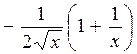 . 336.
. 336. 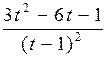 . 337.
. 337. 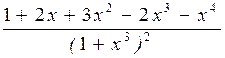 .
.
338. 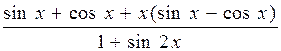 . 339.
. 339. 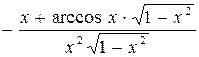 .
.
340. 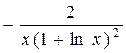 . 341. 3x2 – 3xln3. 342. ex(x2 + 1). 343.
. 341. 3x2 – 3xln3. 342. ex(x2 + 1). 343. 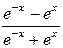 .
.
344. 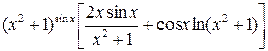 . 345.
. 345. 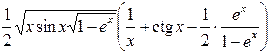 .
.
347. 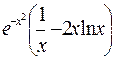 . 346. sin53x·cos33x. 348.
. 346. sin53x·cos33x. 348. 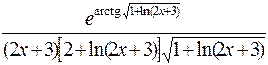 .
.
349. 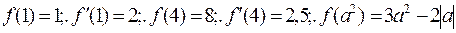 ;
; 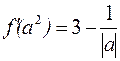 .
.
350. 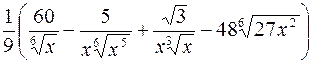 . 351.
. 351. 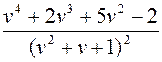 .
.
352. 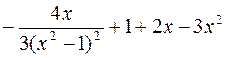 . 353.
. 353. 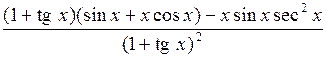 .
.
354. 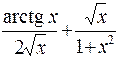 . 355.
. 355. 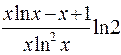 . 356. ex(cos x - sin x).
. 356. ex(cos x - sin x).
357. 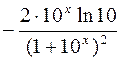 . 358.
. 358. 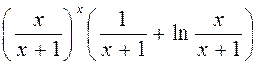 .
.
359. 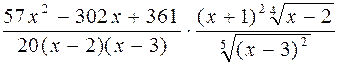 . 360. 2x2e2x+3.
. 360. 2x2e2x+3.
361. 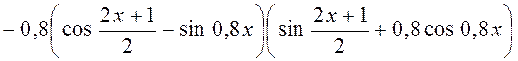 .
.
362. 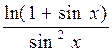 . 363.
. 363. 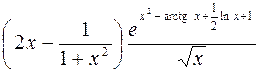 .
.
364. 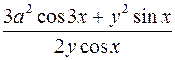 . 365.
. 365. 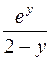 .
.
366. 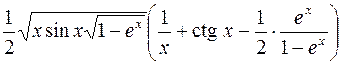 .
.
367. 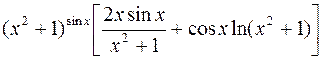 .
.
368. 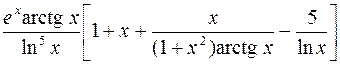 .
.
369. (2; 4). 370. x – y – 3e–2 = 0. 371. 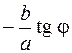 . 372.
. 372. 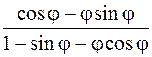 .
.
373. 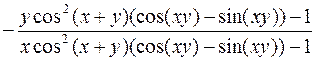 . 374.
. 374. 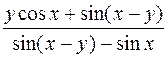 .
.
375. 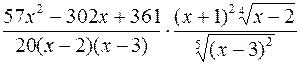 . 376.
. 376. 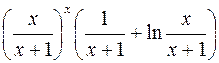 .
.
377. 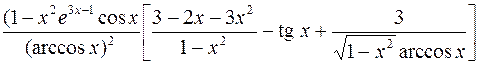 .
.
378. Касательная x + 2y = 4a, нормаль y = 2x – 3a. 379. x + 25y = 0,
x + y = 0. 380. 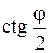 . 381.
. 381. 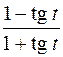 382. 1)
382. 1) 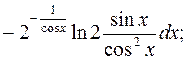
2) 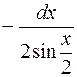 . 383. 0,355. 384.
. 383. 0,355. 384. 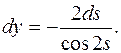 385. 207360. 386.
385. 207360. 386. 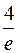
387. 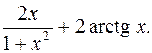 388.
388. 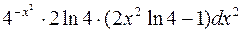 .
.
389. 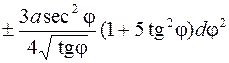 . 390. 1)
. 390. 1) 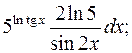
2) 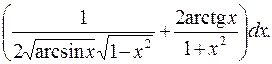 391. 0,995. 392.
391. 0,995. 392. 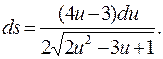
393. 360. 394. 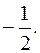 395.
395. 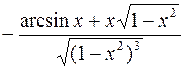 . 396.
. 396. 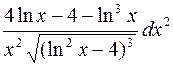 .
.
397. 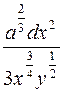 398. 0. 399. cosa. 400. 1. 401. a. 402. 0,5. 403.
398. 0. 399. cosa. 400. 1. 401. a. 402. 0,5. 403. 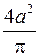 .
.
404. 1. 405. 1. 406. e. 407. e2. 408. 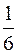 . 409. 3. 410. 0. 411. 1.
. 409. 3. 410. 0. 411. 1.
412. 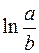 . 413.
. 413. 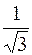 . 414.
. 414. 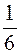 . 415. 1. 416. -0,5. 417. 1. 418. -2.
. 415. 1. 416. -0,5. 417. 1. 418. -2.
419. 0. 420. 0. 421. ¥. 422. 1. 423 1. 424. 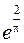 . 425. 1. 426.
. 425. 1. 426. 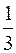 . 427. 1.
. 427. 1.
428. 1. 429. 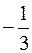 . 430. -2. 431.
. 430. -2. 431. 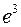 . 432. 10 и 6. 433. 0,6 и –1.
. 432. 10 и 6. 433. 0,6 и –1.
434. 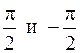 . 435.
. 435. 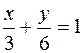 . 436. Сечение желоба имеет форму полукруга. 437. 8 и 0. 438. 1 и 0,6. 439. Наибольшее значение равно 1,
. 436. Сечение желоба имеет форму полукруга. 437. 8 и 0. 438. 1 и 0,6. 439. Наибольшее значение равно 1,
наименьшего – нет. 440. 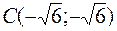 . 441. На высоте
. 441. На высоте 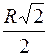 .
.
442. (–¥; 0), (0; 0,5), (1; ¥) – убывает, (0,5; 1) – возрастает; ymin(0,5) = 8,
ymax(1) = 10. 443. (0; 1), (1; e) – убывает, (e; ¥) – возрастает; ymin(e) = e.
444. ymax(0) = 0, ymin(1) = 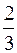 . 445. ymax(–a) = –2a, ymin(a) = 2a.
. 445. ymax(–a) = –2a, ymin(a) = 2a.
446. 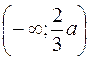 , (a; ¥) – возрастает,
, (a; ¥) – возрастает, 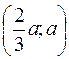 – убывает,
– убывает, 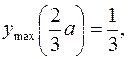
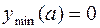 . 447. (–¥;0), (2;¥) – убывает, (0;2) – возрастает, ymin(0) = 0, ymax(2) =
. 447. (–¥;0), (2;¥) – убывает, (0;2) – возрастает, ymin(0) = 0, ymax(2) = 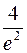 . 448.
. 448. 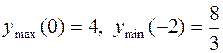 . 449. ymin(0) = 0.
. 449. ymin(0) = 0.
450. 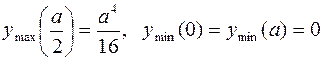 . 451. точки перегиба (2; 62) и (4; 206). Интервалы: вогнутости – (–¥; 2), выпуклости – (2; 4), вогнутости – (4; ¥). 452. точки перегиба (±1; ln 2). Интервалы: выпуклости – (–¥; –1), вогнутости – (–1; 1), выпуклости – (1; ¥).
. 451. точки перегиба (2; 62) и (4; 206). Интервалы: вогнутости – (–¥; 2), выпуклости – (2; 4), вогнутости – (4; ¥). 452. точки перегиба (±1; ln 2). Интервалы: выпуклости – (–¥; –1), вогнутости – (–1; 1), выпуклости – (1; ¥).
453. x = –1, y = 0,5x –1. 454. x = 0, y = x + 3. 455. Точки перегиба 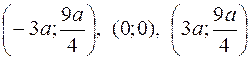 . Интервалы: вогнутости – (–¥;–3a), выпуклости – (0;3a), выпуклости – (3a;¥). 456. Точки перегиба
. Интервалы: вогнутости – (–¥;–3a), выпуклости – (0;3a), выпуклости – (3a;¥). 456. Точки перегиба 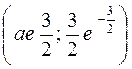 . Интервалы: выпуклости –
. Интервалы: выпуклости – 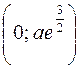 , вогнутости –
, вогнутости – 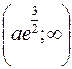 . 457. x = b, x = 2b, y = x +3(b – a). 458. y +1 = 0, 2x + y +1 = 0.
. 457. x = b, x = 2b, y = x +3(b – a). 458. y +1 = 0, 2x + y +1 = 0.
459. Определена везде. График симметричен относительно начала. ymax = 0,5 при x = 1, ymin = – 0,5 при x = –1. Точки перегиба графика 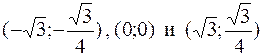 . Асимптота у = 0. 460. Определена везде. График симметричен относительно начала координат.
. Асимптота у = 0. 460. Определена везде. График симметричен относительно начала координат. 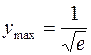 при x = 1,
при x = 1, 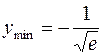 при x = –1. Точки перегиба графика (0; 0),
при x = –1. Точки перегиба графика (0; 0), 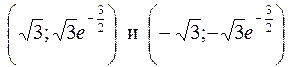 . Асимптота у = 0. 461. Определена везде, кроме х = 0; y = 3 при x = 0,5. Максимумов нет. Точка перегиба графика
. Асимптота у = 0. 461. Определена везде, кроме х = 0; y = 3 при x = 0,5. Максимумов нет. Точка перегиба графика 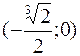 . Асимптота х = 0. 462. Определена везде, график симметричен относительно оси ординат. ymin = –1 при x = 0; (1; 0) и
. Асимптота х = 0. 462. Определена везде, график симметричен относительно оси ординат. ymin = –1 при x = 0; (1; 0) и
(–1; 0) - точки перегиба графика с горизонтальной касательной;
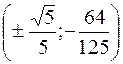 - точки перегиба. Асимптот нет. 463. Определена везде, кроме x = –1;
- точки перегиба. Асимптот нет. 463. Определена везде, кроме x = –1; 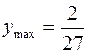 при x = 5, ymin = 0 при x = 1. Абсциссы точек перегиба графика
при x = 5, ymin = 0 при x = 1. Абсциссы точек перегиба графика 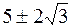 . Асимптоты x = –1 и y = 0. 464. Определена везде, кроме x = 0. Максимумов нет.
. Асимптоты x = –1 и y = 0. 464. Определена везде, кроме x = 0. Максимумов нет. 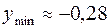 при
при 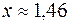 . Абсцисса точки перегиба графика
. Абсцисса точки перегиба графика 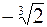 . Асимптота x = 0. 465. Определена везде, кроме значений x = ± 1. График симметричен относительно оси ординат. Максимумов нет. ymin = 1 при x = 0. Точек перегиба нет. Асимптоты x = ± 1, y = 0. 466. Определена везде, кроме x = 1. Максимумов нет.
. Асимптота x = 0. 465. Определена везде, кроме значений x = ± 1. График симметричен относительно оси ординат. Максимумов нет. ymin = 1 при x = 0. Точек перегиба нет. Асимптоты x = ± 1, y = 0. 466. Определена везде, кроме x = 1. Максимумов нет. 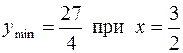 . Точка перегиба графика (0; 0). Асимптота x = 1. 467. Определена везде.
. Точка перегиба графика (0; 0). Асимптота x = 1. 467. Определена везде. 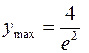 при x = 2, ymin = 0 при x = 0. Абсциссы точек перегиба графика
при x = 2, ymin = 0 при x = 0. Абсциссы точек перегиба графика 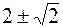 . Асимптота y = 0.
. Асимптота y = 0.
468. Определена везде, кроме x = 1. Максимумов нет. ymin = –1 при x = 0. Точка перегиба графика 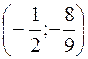 . Асимптоты x = 1 и y = 0.
. Асимптоты x = 1 и y = 0.
469. Определена везде. 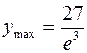 при x = 3. Минимумов нет. Абсциссы точек перегиба 0 и
при x = 3. Минимумов нет. Абсциссы точек перегиба 0 и 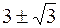 . Асимптота y = 0. 470. Определена везде.
. Асимптота y = 0. 470. Определена везде. 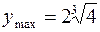 при x = 4, ymin = 0 при x = 0. Точка перегиба графика (6; 0).
при x = 4, ymin = 0 при x = 0. Точка перегиба графика (6; 0).
Асимптота x + y = 2.
