Формула Тейлора для функции нескольких переменных
ВАРИАНТ
Пусть функция f ( x) имеет в точке а и некоторой её окрестности производные порядка n + 1. Пусть x ≠ a есть любое значение аргумента из указанной окрестности, тогда между точками а и х найдётся такая точка с, что справедлива формула
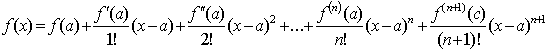 .
.
Доказательство. Положим
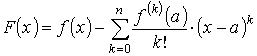 ,
, 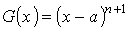 .
.
Функция F(x) имеет производные до порядка n + 1 вместе с функцией f (x). Функция G(x) имеет производные всех порядков, причём её производные положительны при х > a. Легко проверить, что
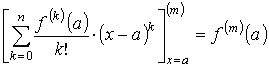 ,
,
и поэтому F (m)(а) = f (m)(а) – f (m)(а) = 0 при m = 0, 1, …, n. Так как G(m)(а) = 0 при m = 0, 1, …, n, то выполнены все условия обобщённой формулы Коши. При этом очевидно, что
F (n + 1)(х) = f (n + 1)(х), G(n + 1)(х) = (n + 1)!
Применение обобщённой формулы Коши к этим функциям приводит к соотношению
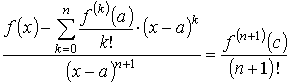 ,
,
откуда и получается формула Тейлора с остаточным членом в форме Лагранжа
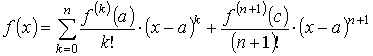 .
.
Как видно, функция раскладывается на две части. Главная часть
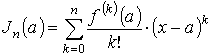
называется многочленом Тейлора порядка n. Второе слагаемое
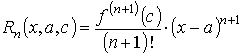
называется остаточным членом функции в форме Лагранжа.
Если в формуле Тейлора положить а = 0, то последняя обращается в формулу Маклорена
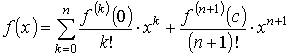 ,
,
где с  (0; х). Формула Тейлора позволяет функцию f (x), возможно, сложной природы, заменить приблизительно сравнительно простой функцией — многочленом.
(0; х). Формула Тейлора позволяет функцию f (x), возможно, сложной природы, заменить приблизительно сравнительно простой функцией — многочленом.
ВАРИАНТ
Как известно, функцию F(t) при условии существования ее производных по порядок n+1 можно разложить по формуле Тейлора с остаточным членом в форме Лагранжа (см. формулы (21.7), (21.11) первой части курса). Запишем эту формулу в дифференциальной форме:
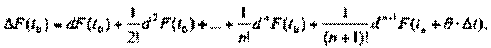 (4.3)
(4.3)
где 
В этой форме формулу Тейлора можно распространить на случай функции нескольких переменных.
Рассмотрим функцию двух переменных f(x, y), имеющую в окрестности точки (х0 , у0) непрерывные производные по (n + 1)-й порядок включительно. Зададим аргументам х и у некоторые приращения Δх и Δу и рассмотрим новую независимую переменную t:
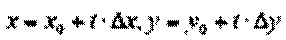 (0 ≤ t ≤1). Эти формулы задают прямолинейный отрезок, соединяющий точки (х0 , у0) и (х0 + Δх, у0 + Δу). Тогда вместо приращения Δf (x0 ,y0) можно рассматривать приращение вспомогательной функции
(0 ≤ t ≤1). Эти формулы задают прямолинейный отрезок, соединяющий точки (х0 , у0) и (х0 + Δх, у0 + Δу). Тогда вместо приращения Δf (x0 ,y0) можно рассматривать приращение вспомогательной функции
F(t) = f (x0 + t Δx, y0 + tΔy) , (4.4)
равное ΔF (0) = F (1) – F (0). Но F (t) является функцией одной переменной t, следовательно, к ней применима формула (4.3). Получаем:
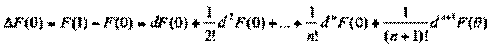 .
.
Отметим, что при линейной замене переменных дифференциалы высших порядков обладают свойством инвариантности, то есть
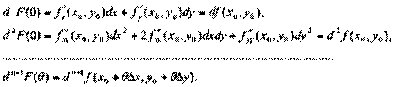
Подставив эти выражения в (4.3), получим формулу Тейлора для функции двух переменных:
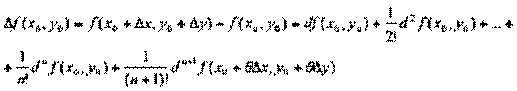 , (4.5)
, (4.5)
где 0<θ<1.
Замечание. В дифференциальной форме формула Тейлора для случая нескольких переменных выглядит достаточно просто, однако в развернутом виде она весьма громоздка. Например, даже для функции двух переменных первые ее члена выглядят так:

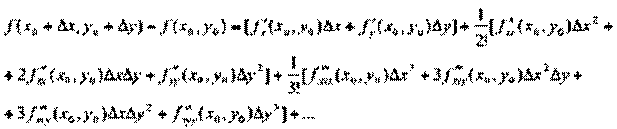
- Приложения формулы Тейлора к исследованию функций:
- Возрастание и убывание функции. Достаточное условие возрастания.

Очень важную информацию о поведении функции предоставляют промежутки возрастания и убывания. Их нахождение является частью процесса исследования функции и построения графика. К тому же точкам экстремума, в которых происходит смена с возрастания на убывание или с убывания на возрастание, уделяется особое внимание при нахождении наибольшего и наименьшего значения функции на некотором интервале.
В этой статье дадим необходимые определения, сформулируем достаточный признак возрастания и убывания функции на интервале и достаточные условия существования экстремума, применим всю эту теорию к решению примеров и задач.
Рекомендуем при необходимости обращаться к разделу дифференцирование функции, так как все признаки в этой статье основаны на нахождении производной.
