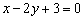П.6.1. Прямые на плоскости

Обозначения: прямые обозначаются маленькими латинскими буквами: .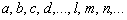

Поскольку любая прямая однозначно определяется двумя точками, то её можно обозначать данными точками: 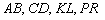и т.д.

Обозначение 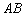совершенно очевидно подразумевает, что точки 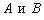принадлежат прямой .

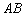1.Уравнение прямой по угловому коэффициенту и точке:

Если известна точка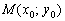 , принадлежащая некоторой прямой, и угловой коэффициент 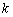этой прямой, то уравнение данной прямой выражается формулой:

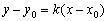
Пример 1. Составить уравнение прямой с угловым коэффициентом 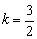, если известно, что точка 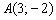принадлежит данной прямой.

Решение: Уравнение прямой составим по формуле .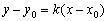

В данном случае:

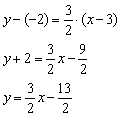
Ответ: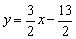

2.Общее уравнение прямой: 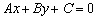, где 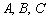– некоторые числа.

При этом коэффициенты 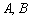одновременно не равны нулю, так как уравнение теряет смысл.

От предыдущей формы уравнения прямой с угловым коэффициентом к общей форме прямой перейти просто:

Например у нас есть уравнение с угловым коэффициентом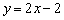

Меняем знаки:

.

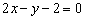Запомните ! Первый коэффициент (чаще всего 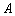) делаем положительным!

В аналитической геометрии уравнение прямой почти всегда будет задано в общей форме.

Ну, а при необходимости его легко привести к «школьному» виду с угловым коэффициентом 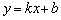(за исключением прямых, параллельных оси ординат).

Переходим к третьему виду уравнения прямой. Мы можем описать прямую, зная ее наклон по отношению, например, к оси X. У каждой прямой есть вполне определённый наклон, который, как мы знаем из Лекции1, может быть описан вектором.

Опр. 6.1. Вектор, который параллелен прямой, называется направляющим вектором данной прямой.

Очевидно, что у любой прямой бесконечно много направляющих векторов, причём все они будут коллинеарны (сонаправлены или нет – неважно).

Направляющий вектор будем обозначать следующим образом: .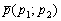

Но одного вектора недостаточно для построения прямой, вектор является свободным и не привязан к какой-либо точке плоскости. Поэтому дополнительно необходимо знать некоторую точку 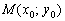, которая принадлежит прямой.

3.Уравнение прямой по точке и направляющему вектору:

Если известна некоторая точка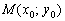 , принадлежащая прямой, и направляющий вектор 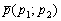этой прямой, то уравнение данной прямой можно составить по формуле:

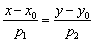
Иногда его называют каноническим уравнением прямой.

Пример 2.

Составить уравнение прямой по точке 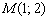и направляющему вектору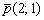

Решение: Уравнение прямой составим по формуле 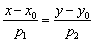. В данном случае:

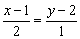
С помощью свойств пропорции избавляемся от дробей:

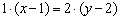
И приводим уравнение к общему виду:

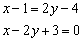
Ответ: