Формулы аналитической геометрии в пространстве
d = √(x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2
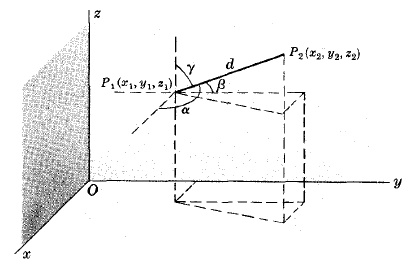
НАПРАВЛЯЮЩИЙ КОСИНУС ЛИНИИ, СОЕДИНЯЮЩЕЯ ТОЧКИ P1(x1,y1,z1) И P2(x2,y2,z2)
l = cosα = (x2 - x1)/d, m = cosβ = (y2 - y1)/d, n = cosγ = (z2 - z1)/d
где α,β,γ углы, которые линия P1P2 образовывает с положительными осями x, y, z соответственно, а d определено на рисунке вверху.
ОТНОШЕНИЕ МЕЖДУ НАПРЯВЛЯЮЩИМИ КОСИНУСАМИ
cos2α + cos2β + cos2γ = 1 или l2 + m2 + n2 = 1
НАПРАВЛЯЮЩИЕ ЧИСЛА
Числа L, M, N, которые есть пропорциональны к направляющим косинусам l, m, n называются направляющими числами. Отношение между ними
l = L/(√L2 + M2 + N 2, m = M/(√L2 + M2 + N 2, n = N/(√L2 + M2 + N 2
УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ P1(x1,y1,z1) И P2(x2,y2,z2) В СТАНДАРТНОЙ ФОРМЕ
(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1) = (z - z1)/(z2 - z1) или (x - x1)/l = (y - y1)/m = (z - z1)/n
. Это также действительно, если l, m, n заменяются на L, M, N соответственно.
УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ P1(x1,y1,z1) И P2(x2,y2,z2) В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
x = x1 + lt, y = y1 + mt, z = z1 + nt
Это также действительно если l, m, n заменяются на L, M, N соответственно.
УГОЛ φ МЕЖДУ ДВУМЯ ЛИНЯМИ С НАПРАВЛЯЮЩИМИ КОСИНУСАМИ l1, m1, n1 И l2, m2, n2
cosφ = l1l2 + m1m2 + n1n2
ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
Ax + By + Cz + D = 0 [A, B, C, D - постоянные]
УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ (x1,y1,z1), (x2,y2,z2), (x3,y3,z3)
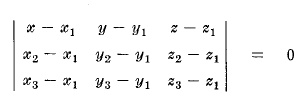
or
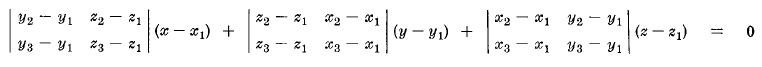
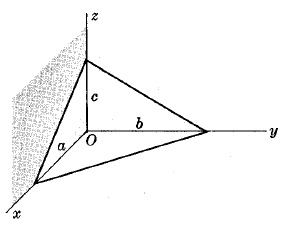
УРАВНЕНИЕ ПЛОСКОСТИ В ФОРМЕ ПЕРЕСЕЧЕНИЯ
x/a + y/b + z/c = 1
где a, b, c есть пересечения на осях x, y, z соответственно.
УРАВНЕНИЕ ЛИНИИ ЧЕРЕЗ (x0,y0,z0) И ПЕРПЕНДИКУЛЯРНОЙ К ПЛОСКОСТИ Ax + By + Cz + D = 0
(x - x0)/A = (y - y0)/B = (z - z0)/C или x = x0 + At, y = y0 + Bt, z = z0 + Ct
. Обратите внимание, что направляющие числа для линии, перпендикулярной к плоскости Ax + By + Cz + D = 0 есть A, B, C.
РАССТОЯНИЕ ОТ ТОЧКИ (x0,y0,z0) К ПЛОСКОСТИ Ax + By + Cz + D = 0.
(Ax0 + By0 + Cz0 + D)/± √A2 + B2 + C2
где знак выбирается так, что расстояние не является отрицательным.
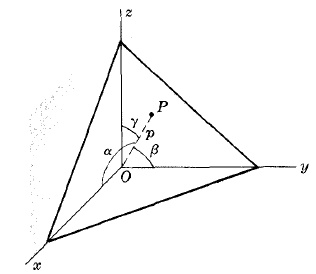
ОБЫЧНАЯ ФОРМА УРАВНЕНИЯ ПЛОСКОСТИ
xcosα + ycosβ + zcosγ = p
где p = перпендикулярному расстоянию от O к плоскости в P и α, β, γ есть углами между OP и положительными осями x, y, z.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПРОСТОМ ПЕРЕМЕЩЕНИИ
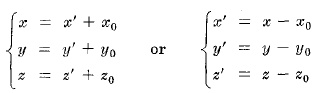
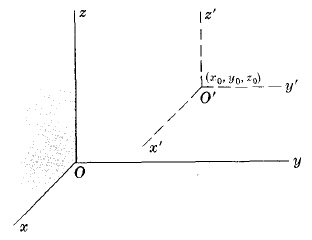
где (x, y, z) - старые координаты [т.e. координаты относительно системы xyz],(x', y', z') - новые координаты [относительно системы x'y'z'] и (x0,y0,z0) координаты нового центра O' относительно старой координатной системы xyz.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПРОСТОМ ВРАЩЕНИИ
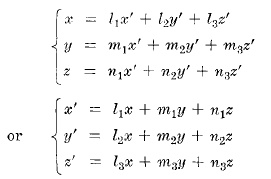
где центры систем xyz и x'y'z' находятся в одной точке и l1,m1,n1; l2,m2,n2; l3,m3,n2 направляющие косинусы осей x', y', z' относительно осей x, y, z соответственно.
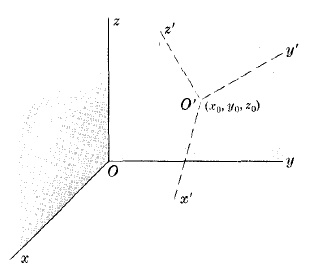
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ И ВРАЩЕНИИ
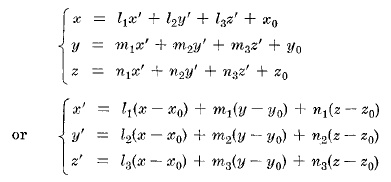
где O' системы x'y'z' имеет координаты (x0,y0,z0) относительно системы xyz и l1,m1,n1; l2,m2,n2; l3,m3,n2 направляющие косинусы осей x', y', z' относительно осей x, y, z соответственно.
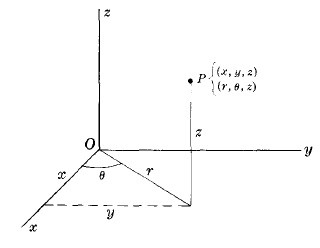
ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ (r, θ, z)
Точка P может быть определена как цилиндрическими координатами (r, θ, z), так и прямоугольными координатами (x, y, z).
Преобразование между этими двумя координатами есть
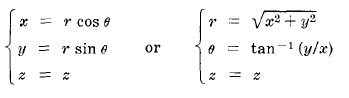
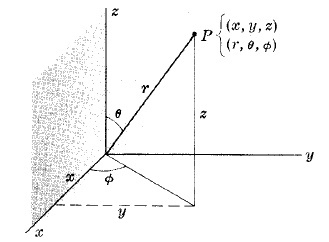
СФЕРИЧЕСКИЕ КООРДИНАТЫ (r, θ, φ)
Точка P может быть определена как сферическими координатами (r, θ, φ) так и прямоугольными координатами (x, y, z).
Преобразование между этими двумя кординатами есть
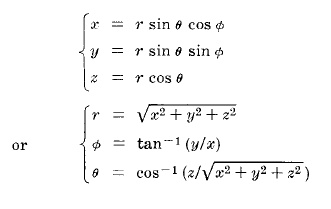
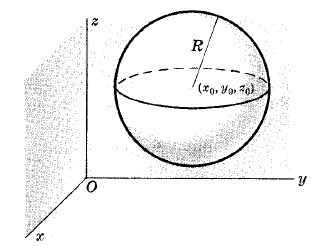
УРАВНЕНИЕ СФЕРЫ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
(x - x0)2 + (y - y0)2 + (z - z0)2 = R2
где сфера имеет центр (x0,y0,z0) и радиус R.
УРАВНЕНИЕ СФЕРЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
r2 - 2r0r(θ - θ0) + r02 + (z - z0)2 = R2
где сфера имеет центр (r0,θ0,z0) в цилиндрических координатах и радиус R.
Если центр находится в начале координат, уравнение имеет вид:
r2 + z2 = R2
УРАВНЕНИЕ СФЕРЫ В СФЕРИЧЕСКИХ КООРДИНАТАХ
r2 + r02 - 2r0rsinθsinθ0cos(φ - φ0) = R2
где сфера имеет центр(r0,θ0,φ0) в сферических координатах и радиус R.
Если центр в начале координат, уравнение имеет вид:
r = R.
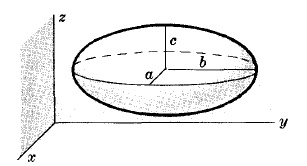
УРАВНЕНИЕ ЭЛЛИПСОИДА С ЦЕНТРОМ (x0,y0,z0) И ПОЛУОСЯМИ a, b, c
(x - x0)2/a2 + (y - y0)2/b2 + (z - z0)2/c2 = 1
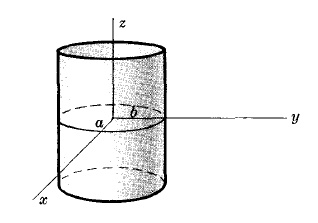
ЭЛЛИПТИЧЕСКИЙ ЦИЛИНДР С ОСЬЮ КАК z ОСЬ
x2/a2 + y2/b2 = 1
где a, b - полуоси эллиптического сечения.
Если b = a, фигура превращается в цилиндрический цилиндр с радиусом a.
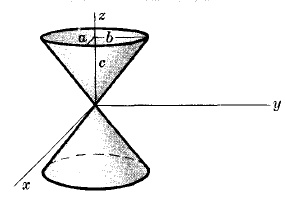
ЭЛЛИПТИЧЕСКИЙ КОНУС С ОСЬЮ КАК z ОСЬ
x2/a2 + y2/b2 = z2/c2
ОДНОПОЛОСТНЫЙ ГИПЕРБОЛОИД
x2/a2 + y2/b2 - z2/c2 = 1.
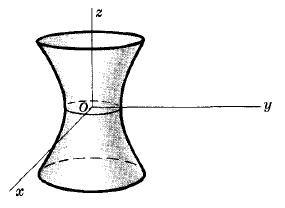
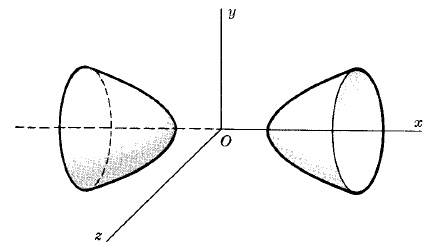
ДВУПОЛОСТНЫЙ ГИПЕРБОЛОИД
x2/a2 - y2/b2 - z2/c2 = 1.
ЭЛЛИПТИЧЕСКИЙ ПАРАБОЛОИД
x2/a2 + y2/b2 = z/c

ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД
x2/a2 - y2/b2 = z/c
. Обратите внимание на ориентацию осей этой фигуры.