Образец выполнения задания № 2
Контрольная работа № 10
Контрольная работа № 10 состоит из четырех заданий. Ниже подробно рассмотрены варианты решения заданий.
Образец выполнения задания № 1
Задача.При проведении испытаний материала на разрыв 50 значений, характеризующих прочность на разрыв. По этим данным составлен сгруппированный вариационный ряд (табл. 1; масштаб  Па).
Па).
Таблица 1
 | 120-140 | 140-160 | 160-180 | 180-200 | 200-220 | 220-240 | 240-260 | 260-280 |
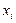 | ||||||||
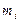 |
Оценить согласие полученных данных с нормальным распределением при уровне значимости  и получить приближенную интервальную оценку для параметра
и получить приближенную интервальную оценку для параметра  с надежностью
с надежностью  .
.
Решение.Введем условную варианту, определим шаг 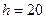 и выбрав ложный нуль
и выбрав ложный нуль  , и найдем
, и найдем  и
и  (см. табл.2 )
(см. табл.2 )
Таблица 2
 | 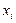 | 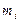 | 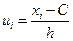 | 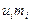 | 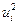 |  |
| -3 -2 -1 | -6 -8 -10 | |||||
 |
По данным этой таблицы имеем 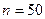 и
и
 ,
,
 ,
,

Найдем теоретические частоты для интервалов  , используя формулу вероятности попадания значений в этот интервал:
, используя формулу вероятности попадания значений в этот интервал: 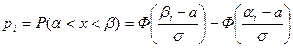 .
.
Для нормального распределения с параметрами  и
и 
Таблица 3
 |  | 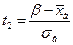 | 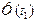 |  | 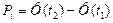 | 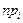 |
| 120-140 140-160 160-180 180-200 200-220 220-240 240-260 260-280 | -2,43 -1,78 -1,13 -0,48 0,17 0,81 1,46 2,11 | -1,78 -1,13 -0,48 0,17 0,81 1,46 2,11 2,73 | -0,4924 -0,4624 -0,3708 -0,1844 0,0675 0,2910 0,4279 0,4826 | 0,4624 -0,3708 -0,1844 0,0675 0,2910 0,4279 0,4826 0,4968 | 0,0300 0,0916 0,1864 0,2519 0,2235 0,1369 0,0547 0,0142 | 1,5≈1 4,58≈5 9,34≈9 12,59≈13 11,17≈11 6,87≈7 2,78≈3 0,71≈1 |
Найдем выборочное значение  , объединив крайние интервалы для маленьких частот
, объединив крайние интервалы для маленьких частот 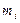 (табл. 4)
(табл. 4)
Таблица 4
Номер  | Границы  | 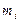 | 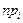 | 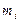 - - 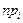 |  |  |
| 120-140 140-160 160-180 180-200 200-220 220-240 240-260 260-280 | 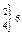 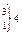 | 0,111 0,143 | ||||
 |  =0,254 =0,254 |
Так как теперь, после объединения, число интервалов  , а число наложенных связей
, а число наложенных связей 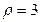 , то число степеней свободы
, то число степеней свободы 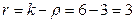 и поэтому по таблице критических значений
и поэтому по таблице критических значений 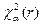 имеем
имеем 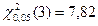 . Сравнивая найденное значение
. Сравнивая найденное значение 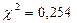 с критическим (0,254<7,82), определяем, что рассматриваемые данные можно считать полученными из нормально распределенной совокупности.
с критическим (0,254<7,82), определяем, что рассматриваемые данные можно считать полученными из нормально распределенной совокупности.
Для получения интервальной оценки найдем  из условия
из условия 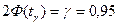 ,т.е.
,т.е. 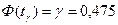 и
и  , и радиус интервала
, и радиус интервала 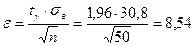 .
.
Доверительный интервал для параметра  с надежностью
с надежностью  есть:
есть:
 .
.
Пусть для изучаемой системы случайных величин (X,Y) получена выборка значений выборки  , каждое значение X, встречается с частотой
, каждое значение X, встречается с частотой  , а каждое значение
, а каждое значение 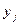 встречается соответственно с частотой
встречается соответственно с частотой  . Условные средние
. Условные средние 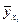 и
и  представляют отдельные значения для регрессий, соответственно, Yна Xи Xна Y:
представляют отдельные значения для регрессий, соответственно, Yна Xи Xна Y:
 ,
,  .
.
Образец выполнения задания № 2
Задача.Даны выборочные варианты 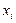 и соответственные частоты
и соответственные частоты 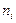 количественного признака Х:
количественного признака Х:
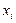 10 15 20 25 30
10 15 20 25 30
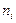 6 16 50 24 4
6 16 50 24 4
Найти методом произведений выборочные среднюю, дисперсию и среднее квадратическое отклонение.
Решение.Составим расчетную таблицу, для чего:
1) запишем варианты 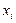 в первый столбец;
в первый столбец;
2) запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца;
3) в качестве ложного нуля С выберем варианту 20 (эта варианта имеет наибольшую частоту); в клетке третьего столбца, которая принадлежит строке, содержащей варианту 20,пишем 0; над нулем последовательно записываем условные варианты -1, -2, а под нулем – последовательно 1,2;
4) произведения частот на условные варианты 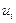 записываем в четвертый столбец; отдельно находим сумму (-28) отрицательных и отдельно сумму (32) положительных чисел; сложив эти числа, их сумму (4) помещаем в нижнюю клетку столбца;
записываем в четвертый столбец; отдельно находим сумму (-28) отрицательных и отдельно сумму (32) положительных чисел; сложив эти числа, их сумму (4) помещаем в нижнюю клетку столбца;
5) произведения частот на квадраты условных вариант запишем в пятый столбец; сумму чисел столбца (80) помещаем в нижнюю клетку столбца;
6) произведения частот на квадраты условных вариант, увеличенных на единицу, запишем в шестой (контрольный) столбец, сумму чисел столбца (188) помещаем в нижнюю клетку столбца.
В итоге получим следующую расчетную таблицу:
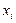 | 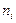 | 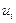 | 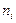 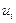 | 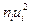 | 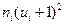 |
| -2 -1 | -12 -16 -28 | ||||
| n=100 | 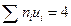 | 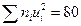 |  |
Контроль:
 ;
;  .
.
Совпадением найденных сумм свидетельствует о том, что вычисления произведены правильно.
Вычислим условные моменты первого и второго порядков:

Найдем шаг (разность между двумя соседними вариантами): 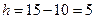 .
.
Найдем искомую выборочную среднюю: 
Найдем искомую выборочную дисперсию: 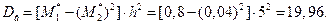
Найдем искомое выборочное среднее квадратическое отклонение:

