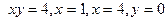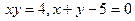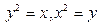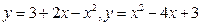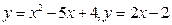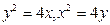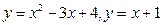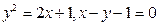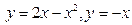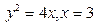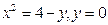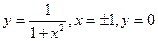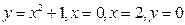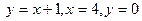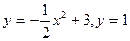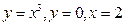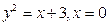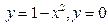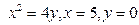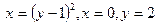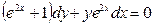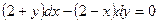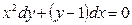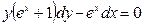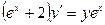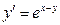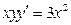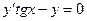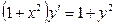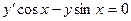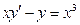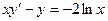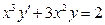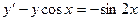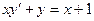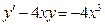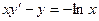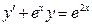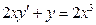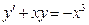Задачи для контрольных работ
Контрольная работа № 1
В задачах 1-20 найти указанные пределы.
1. а) 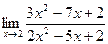 ; б)
; б) 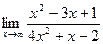 ; в)
; в) 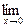
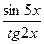 ; г)
; г) 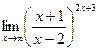
2. a) 
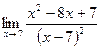 ; б)
; б) 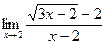 ; в)
; в) 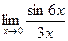 ; г)
; г) 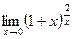 ;
;
3. a) 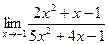 ; б)
; б) 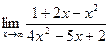 ; в)
; в) 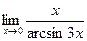 ; г)
; г) 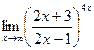 ;
;
4. a) 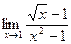 ; б)
; б) 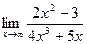 ; в)
; в) 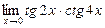 ; г)
; г) 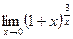 ;
;
5. a) 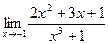 ; б)
; б) 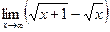 ; в)
; в) 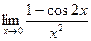 ; г)
; г) 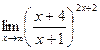 ;
;
6. a) 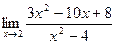 ; б)
; б) 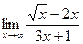 ; в)
; в) 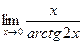 ; г)
; г) 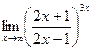 .
.
7. a) 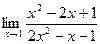 ; б)
; б) 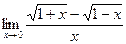 ; в)
; в) 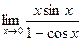 ; г)
; г) 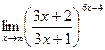 ;
;
8. a) 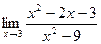 ; б)
; б) 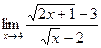 ; в)
; в) 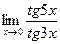 ; г)
; г) 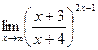 .
.
9. a) 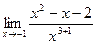 ; б)
; б) 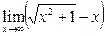 ; в)
; в) 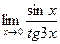 ; г)
; г) 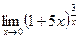 ;
;
10. a) 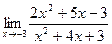 ; б)
; б) 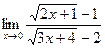 ;в)
;в) 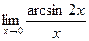 ; г)
; г) 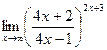 .
.
11. a) 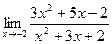 ; б)
; б) 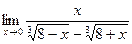 ; в)
; в) 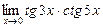 ; г)
; г) 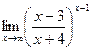 .
.
12. a) 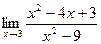 ; б)
; б) 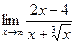 ; в)
; в) 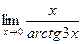 ; г)
; г) 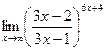 .
.
13. a) 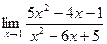 ; б)
; б) 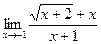 ; в)
; в) 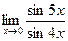 ; г)
; г) 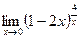 .
.
14. a) 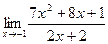 ; б)
; б) 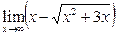 ; в)
; в) 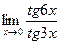 ; г)
; г) 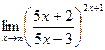 .
.
15. a) 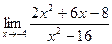 ; б)
; б) 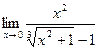 ; в)
; в) 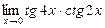 ; г)
; г) 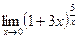 .
.
16. a) 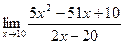 ; б)
; б) 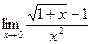 ; в)
; в) 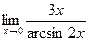 ; г)
; г) 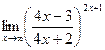 .
.
17. a) 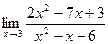 ; б)
; б) 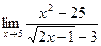 ; в)
; в) 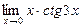 ; г)
; г) 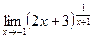 .
.
18. a) 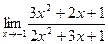 ; б)
; б) 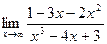 ; в)
; в) 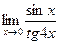 ; г)
; г) 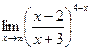 .
.
19. a) 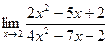 ; б)
; б) 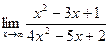 ; в)
; в) 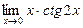 ; г)
; г) 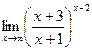 .
.
20. a) 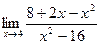 ; б)
; б) 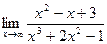 ; в)
; в) 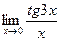 ; г)
; г) 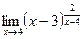 .
.
В задачах 21-40 найти производные функций.
21. а) 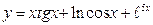 ; б)
; б) 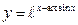 ; в)
; в) 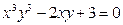 .
.
22. a) 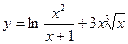 ; б)
; б) 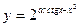 ; в)
; в) 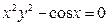 .
.
23. a) 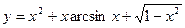 ; б)
; б) 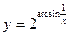 ; в)
; в) 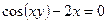 .
.
24. a) 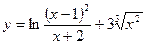 ; б)
; б) 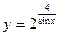 ; в)
; в) 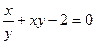 .
.
25. a) 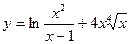 ; б)
; б) 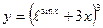 ; в)
; в) 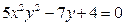 .
.
26. a) 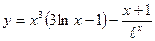 ; б)
; б) 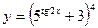 ; в)
; в) 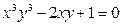 .
.
27. a) 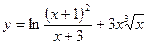 ; б)
; б) 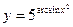 ; в)
; в) 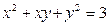 .
.
28. a) 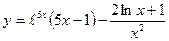 ; б)
; б) 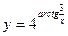 ; в)
; в) 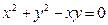 .
.
29. a) 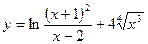 ; б)
; б) 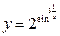 ; в)
; в) 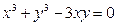 .
.
30. a) 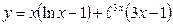 ; б)
; б) 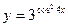 ; в)
; в) 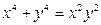 .
.
31. a) 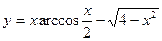 ; б)
; б) 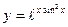 ; в)
; в) 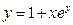 .
.
32. a) 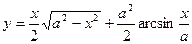 ; б)
; б) 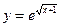 ; в)
; в) 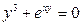 .
.
33. a) 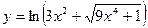 ; б)
; б) 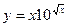 ; в)
; в) 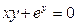 .
.
34. a) 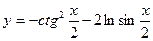 ; б)
; б) 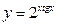 в)
в) 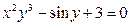 .
.
35. a) 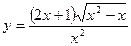 ; б)
; б) 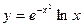 ; в)
; в) 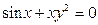 .
.
36. a) 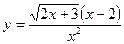 ; б)
; б) 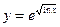 ; в)
; в) 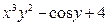 .
.
37. a) 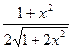 ; б)
; б) 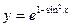 ; в)
; в) 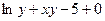 .
.
38. a) 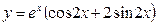 ; б)
; б) 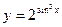 ; в)
; в) 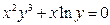 .
.
39. a) 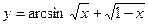 ; б)
; б) 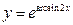
 ; в)
; в) 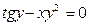 .
.
40. a) 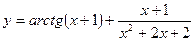 ; б)
; б) 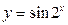 ; в)
; в) 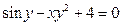 .
.
В задачах 41-60 исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы возрастания и убывания функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции .
41. 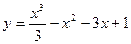 | 42. 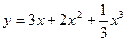 |
43. 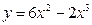 | 44. 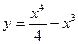 |
45. 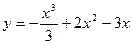 | 46. 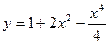 |
47. 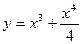 | 48. 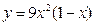 |
49. 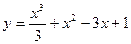 | 50. 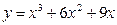 |
51. 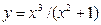 | 52. 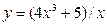 |
53. 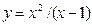 | 54. 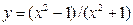 |
55. 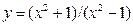 | 56. 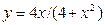 |
57. 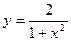 | 58. 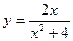 |
59. 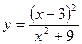 | 60. 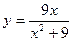 |
В задачах 61-80 задана функция 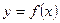 и значения аргумента
и значения аргумента 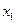 и
и 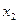 . Найти приближенное значение данной функции при
. Найти приближенное значение данной функции при 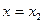 , исходя из ее точного значения при
, исходя из ее точного значения при 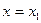 .
.
-
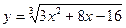 ,
, 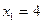 ,
, 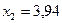 .
. -
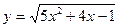 ,
, 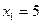 ,
, 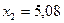 .
. -
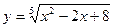 ,
, 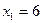 ,
, 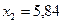 .
. -
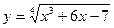 ,
, 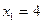 ,
, 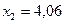 .
. -
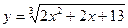 ,
, 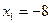 ,.
,. 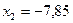
-
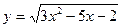 ,
, 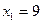 ,
, 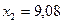 .
. -
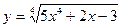 ,
, 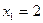 ,
, 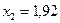 .
. -
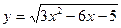 ,
, 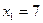 ,
, 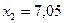 .
. -
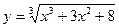 ,
, 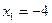 ,
, 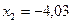 .
. -
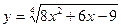 ,
, 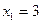 ,
, 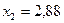 .
. -
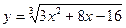 ,
, 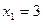 ,
, 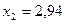
-
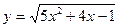 ,
, 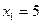 ,
, 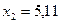
-
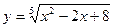 ,
, 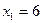 ,
, 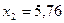
-
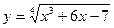 ,
, 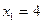 ,
, 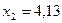
-
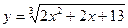 ,
, 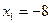 ,
, 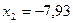
-
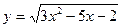 ,
, 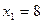 ,
, 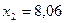
-
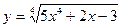 ,
, 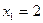 ,
, 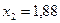
-
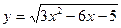 ,
, 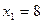 ,
, 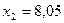
-
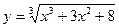 ,
, 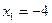 ,
, 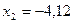
-
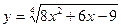 ,
, 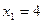 ,
, 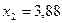
В задачах 81-100вычислить неопределенные интегралы и результаты интегрирования проверить дифференцированием.
81. a) 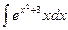 ; б)
; б) 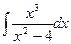 ; в)
; в) 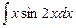 .
.
82. a) 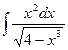 ; б)
; б) 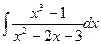 ; в)
; в) 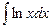 .
.
83. a) 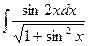 ; б)
; б) 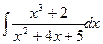 ; в)
; в) 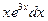 .
.
84. a) 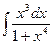 ; б)
; б) 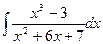 ; в)
; в) 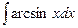 .
.
85. a) 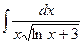 ; б)
; б) 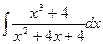 ; в)
; в) 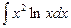 .
.
86. a) 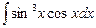 ; б)
; б) 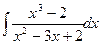 ; в)
; в) 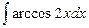 .
.
87. a) 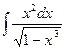 ; б)
; б) 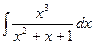 ; в)
; в) 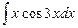 .
.
88. a) 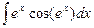 ; б)
; б) 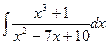 ; в)
; в) 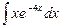 .
.
89. a) 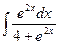 ; б)
; б) 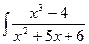 ; в)
; в) 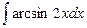 .
.
90. a) 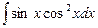 ; б)
; б) 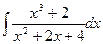 ; в)
; в) 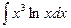 .
.
91. a) 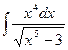 ; б)
; б) 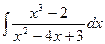 ; в)
; в) 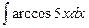 .
.
92. a) 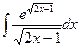 ; б)
; б) 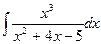 ; в)
; в) 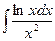 .
.
93. a) 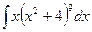 ; б)
; б) 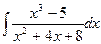 ; в)
; в) 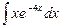 .
.
94. a) 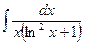 ; б)
; б) 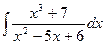 ; в)
; в) 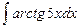 .
.
95. a) 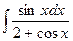 ; б)
; б) 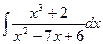 ; в)
; в) 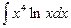 .
.
96. a) 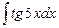 ; б)
; б) 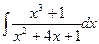 ; в)
; в) 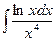 .
.
97. a) 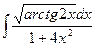 ; б)
; б) 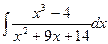 ; в)
; в) 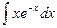 .
.
98. a) 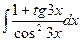 ; б)
; б) 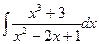 ; в)
; в) 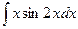 .
.
99. a) 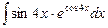 ; б)
; б) 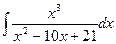 ; в)
; в) 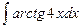 .
.
100. a) 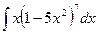 ; б)
; б) 
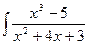 ; в)
; в) 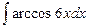 .
.
В задачах 101-120 вычислить площади фигур, ограниченных данными линиями:
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
Контрольная работа №2
В задачах 121-140 данную функцию исследовать на экстремум.
121. 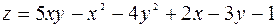
122. 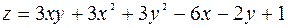
123. 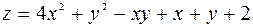
124. 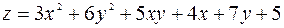
125. 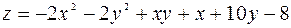
126. 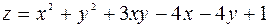
127. 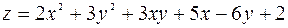
128. 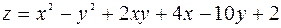
129. 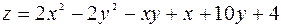
130. 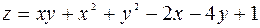
131. 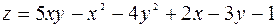
132. 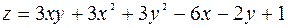
133. 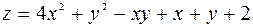
134. 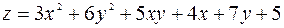
135. 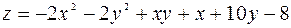
136. 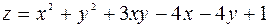
137. 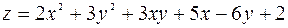
138. 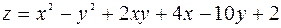
139. 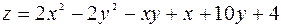
140. 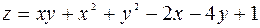
В задачах 141 - 160 найти общее решение дифференциальных уравнений первого порядка.
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
В задачах 161 - 180 найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям.
-
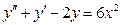 ,
, 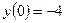 ,
, 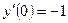 .
. -
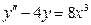 ,
, 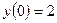 ,
, 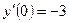 .
. -
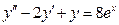 ,
, 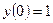 ,
, 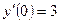 .
. -
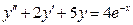 ,
, 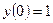 ,
, 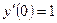 .
. -
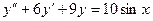 ,
, 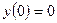 ,
, 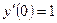 .
. -
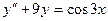 ,
, 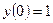 ,
, 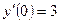 .
. -
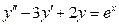 ,
, 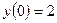 ,
, 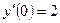 .
. -
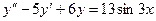 ,
, 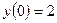 ,
, 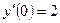 .
. -
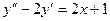 ,
, 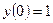 ,
, 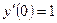 .
. -
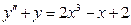 ,
, 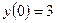 ,
, 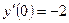 .
. -
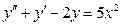 ,
, 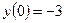 ,
, 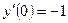
-
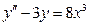 ,
, 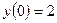 ,
, 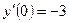
-
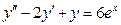 ,
, 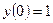 ,
, 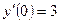
-
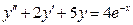 ,
, 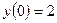 ,
, 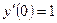
-
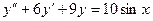 ,
, 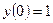 ,
, 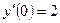
-
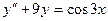 ,
, 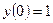 ,
, 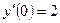
-
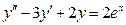 ,
, 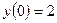 ,
, 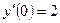
-
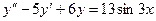 ,
, 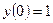 ,
, 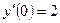
-
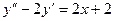 ,
, 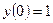 ,
, 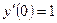
-
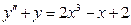 ,
, 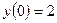 ,
, 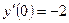
В задачах 181 - 200 написать первыетри члена ряда 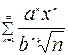 , найти интервал сходимости ряда и исследовать его сходимость на концах интервала, где:
, найти интервал сходимости ряда и исследовать его сходимость на концах интервала, где:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В задачах 201-220 вычислить определенный интеграл с точностью до 0,001 путем разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.
201. 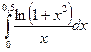 | 202. 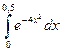 |
203. 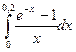 | 204. 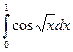 |
205. 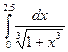 | 206. 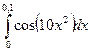 |
207. 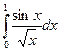 | 208. 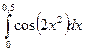 |
209. 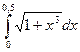 | 210. 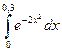 |
211. 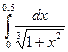 | 212. 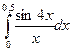 |
213. 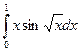 | 214. 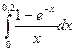 |
215. 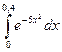 | 216. 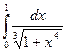 |
217. 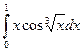 | 218. 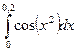 |
219. 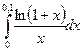 | 220. 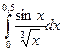 |
Приложение 1
Правила дифференцирования.
1) 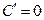 , если
, если 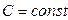 .
.
2) 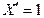 ,
, 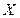 - переменная.
- переменная.
3) 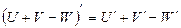 , где
, где 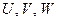 - функции от
- функции от  .
.
4) 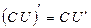 .
.
5) 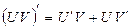 .
.
6) 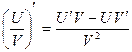 .
.
Таблица производных.
| Элементарные функции | Сложные функции |
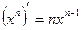 | 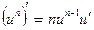 |
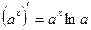 | 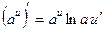 |
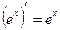 | 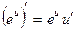 |
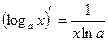 | 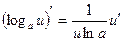 |
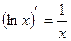 | 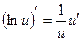 |
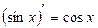 | 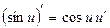 |
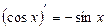 | 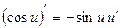 |
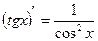 | 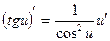 |
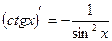 | 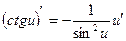 |
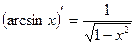 | 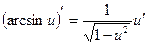 |
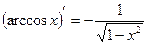 | 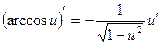 |
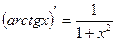 | 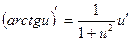 |
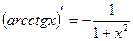 | 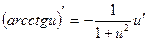 |
Приложение 2
Таблица интегралов
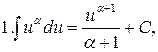 a¹-1 a¹-1 | 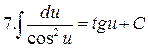 |
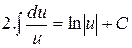 | 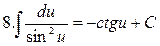 |
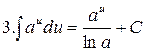 | 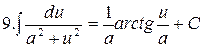 |
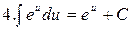 | 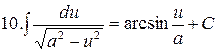 |
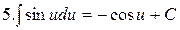 | 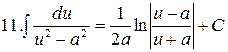 |
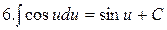  | 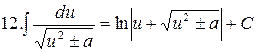 |
Таблица дифференциалов
1. 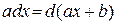 2.
2. 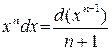 3.
3. 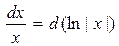
4. 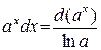 5.
5. 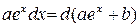 6.
6. 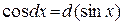
7. 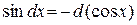 8.
8. 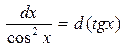 9.
9. 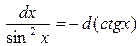
10. 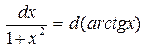 11.
11. 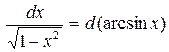 12.
12.