Кручение бруса и прямой изгиб балок – задание № 3

Деформацию кручения стержень испытывает только тогда, когда в поперечном сечении возникает только одно внутреннее усилие – крутящий момент “ 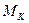”, обусловленный действием касательных напряжений “ 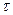”. Кручение происходит под воздействием внешних скручивающих моментов “m”, расположенных в плоскости, перпендикулярной оси стержня (вала). Для определения опасного сечения, в котором действуют наибольшие касательные напряжения, строится эпюра 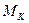, отражающая характер распределения крутящих моментов по длине вала. Условие прочности при кручении:

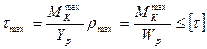(16)

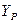где и 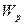- соответственно полярный момент инерции и полярный момент сопротивления сечения кручению;

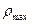- расстояние до крайних (наружных) волокон.

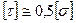- допускаемое касательное напряжение.

Для вала с круглым (сплошным) поперечным сечением

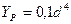, а (17)

где d – диаметр вала.

Для вала с кольцевым поперечным сечением:

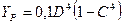, а (18)

где D и d – наружный и внутренний диаметры

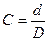- толстостенность кольца.

Условие жесткости при кручении вала имеет вид:

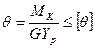(19)

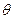где и 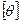- расчетный и допускаемый относительный угол закручивания, 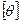= 0,5+4,0 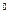/м;

G – модуль упругости при сдвиге, для сталей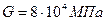

Для определения диаметров вала из условий прочности (16) и жесткости (19) после преобразований с учетом (17) и (18) получим следующие формулы:

для сплошного круглого сечения

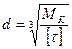; (20)

для кольцевого сечения

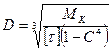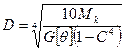; (21)

Из двух величин диаметров вала, полученных расчетом на прочность и жесткость окончательно принимается наибольшее значение и округляется до ГОСтовского размера (кратного 5) до диаметра d= 90 и кратного 10 – диаметром свыше 90 мм.

ПРЯМЫМ ИЗГИБОМ называется такой вид деформации, когда в поперечном сечении возникают внутренние усилия – изгибающий момент и поперечная сила и плоскость из действия совпадает с главной осью инерции поперечного сечения (с осью симметрии). В этой же плоскости действу4ют внешние нагрузки. Изгибающий момент 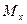обусловлен действием нормальных напряжений, а поперечная сила - касательных напряжений. Расчет на прочность ведут обычно только по нормальным напряжениям:

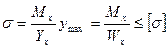(22)

где - максимальный изгибающий момент, действующий в балке;

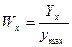и - соответственно осевой момент инерции и осевой момент сопротивления сечения при изгибе;

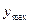- расстояние до крайних (наружных) волокон;

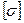- допускаемое напряжение при изгибе.

Для определения опасного сечения, в котором действуют наибольшие нормальные сечения, строятся эпюры 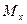и , отражающие характер распределения этих внутренних усилий по участкам балки, построении эпюр 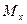и наблюдаются следующие закономерности:

- на участках балки, где нет распределенной нагрузки q =const, а 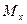меняется линейно, причем если >0, то 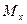возрастает, а при <0, 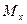убывает;

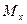- если на участке балки действует распределенная нагрузка (q), то меняется линейно, а по параболе, выпуклость параболы направлена навстречу действия распределенной нагрузки;

- в сечениях, где приложены сосредоточенные силы, на эпюре получаются скачки, по величине и направлению равные этим силам;

- в сечениях, где приложены внешние сосредоточенные моменты скачки, равные этим моментам, получаются при эпюре ;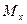

- в сечениях, где происходит через нуль, меняя свой знак, на эпюре 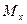имеем экстремальное значение изгибающего момента;

- для удобства эпюру 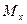будем строить со стороны сжатых волокон.

При прямом изгибе поперечные сечения балки получают линейные (прогибы у) и угловые (угол поворота 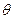) перемещения (см. рис. 42), которые можно определить двумя способами:

Рис. 42.