Дать анкету бинарного отношения, заданного

ориентированным графом G=(V,A), V={1,2,3,4}, A={(2,1),(2,3),(3,3),(4,3),(1,3),(2,4),(1,4),(1,1),(2,2),(4,4)}

Рефлексивность +

Антирефлексивность -

Симметричность -

Антисимметричность +

Асимметричность +

Транзитивность +

Связность +

Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

Задача 9.1.

A={(1,1),(2,2),(3,3),(4,4),(1,3), (3,1),(2,4),(4,2)}

Задача 9.2.

A={(1,1),(2,3),(3,3),(4,3),(1,3),(3,1),(2,4),(4,2)}

Задача 9.3.

A={(2,1),(2,3),(3,3),(4,3),(1,3), (3,1),(2,4),(1,2),(1,1)}

Задача 9.4.

A={(2,1),(2,3),(3,3),(4,3),(1,3),(3,2),(2,4),(1,4),(1,1)}

Задача 9.5.

A={(1,1),(2,2),(3,3),(4,4),(1,3),(3,1),(2,4),(4,2)}

Задача 9.6.

A={(2,1),(2,3),(3,3),(4,3),(1,3),(3,2),(2,4),(1,4),(1,1)}

Задача 9.7.

A={(2,1),(2,3),(3,3),(4,3),(1,3),(3,2),(2,4),(1,4),(1,1),(2,2)}

Задача 9.8.

A={(2,1),(2,3),(3,3),(4,3),(1,3),(2,4),(1,4),(1,1),(2,2)}

Задача 9.9.

A={(2,1),(2,3),(3,3),(4,3),(1,3),(3,2),(2,4),(1,4),(1,1)}

Задача 9.10.

A={(1,2),(2,1),(1,3),(3,1),(2,3),(3,2),(2,4),(4,2)}

3.10. Определить, является ли соответствие Q=(F,A,B), где A=B,

A={1,2,3,4}, а F -график соответствия задается ориентированным графом G функциональным, сюръективным, инъективным, всюду определенным, биективным.

(-,+,-,+,-)

Определить, является ли соответствие Q=(Ф,А,В), где А=В,

A={1,2,3,4}, а Ф - график соответствия задается ориентированным графом G функциональным, сюръективным, инъективным, всюду определенным, биективным ?

Задача 10.1. - Задача 10.10

Графы из условий задач 9.1 -9.10.

Решить систему уравнений.

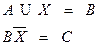
Решение.

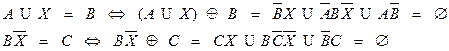
Общее уравнение.

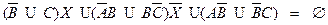
Необходимые и достаточные условия совместности.

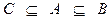
Общее решение.

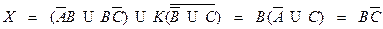
Решение единственно.

Проверка.

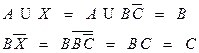
Решить систему уравнений.

Задача 11.1.

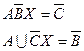
Задача 11.2.

AX=BС

B 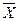=CA

Задача 11.3.

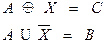
Задача 11.4.

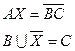
Задача 11.5.

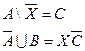
Задача 11.6.

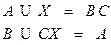
Задача 11.7.

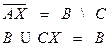
Задача 11.8.

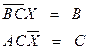
Задача 11.9.

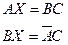
Глава 4. Вопросы к экзамену.

1.Множества. Конечные и бесконечные множества. Способы задания множеств.

2. Подмножества. Множество всех подмножеств данного множества.

3. О числе к-элементных подмножеств n-элементного множества.

4.Определение мощности множества всех подмножеств конечного множества (с использованием формулы бинома Ньютона).

5.Универсальное множество. Понятие алгебры. Алгебра множеств.

6.Понятия алгебраических и кардинальных операций. Алгебраические операции над множествами.

7.Законы алгебры множеств. Двойственность в алгебре множеств.

8.Уравнения и системы уравнений в алгебре множеств. Основные леммы, используемые при решении уравнений в алгебре множеств.

9.Мощность множества. Понятие счетного множества и континуума.

10.Канторовская диагональная процедура. Примеры счетных множеств.

11.Доказательство счетности множества алгебраических чисел.

12.Свойства счетных множеств. Необходимые и достаточные условия бесконечности множества.

13. Примеры континуальных множеств. Теорема Кантора-Бернштейна.

14. Доказательство существования иррациональных и трансцендентных чисел.

15.Кардинальные операции над множествами. Прямое произведение множеств. Проекция множеств.

16.Бинарные отношения. Свойства бинарных отношений. 17.Представления бинарных отношений в виде матриц, орграфов, верхнего и нижнего сечений.

18. Операции над бинарными отношениями. Выражение свойств бинарных отношений через задающие их множества.

19. Отношения порядка. Упорядоченные множества.

20.Отношение эквивалентности. Классы эквивалентности. Системы различных представителей.

21.Лексикографическое отношение порядка.

22.Мажоранта и миноранта множеств. Максимум и минимум множеств. Точные грани множеств.

23.Понятие графика. Функциональные, инъективные графики. Инверсия графика.

24.Соответствия. Функциональные, инъективные, сюръективные и биективные соответствия.

25.Общее понятие функции. Биективная функция.

26.Высказывания. Операции над высказываниями. Формулы и функции алгебры логики.

27.О числе функций алгебры логики от n переменных.

28. Равносильные формулы. Законы алгебры логики.

29.ДНФ и КНФ.

30.Разложение функций алгебры логики по к переменным.

31.СДНФ и СКНФ.

32. Логические следствия. Проблема разрешимости в алгебре логики.

33.Тавтологии и противоречия.

34.Основные схемы доказательств: если x то y, доказательство от противного, доказательство построением цепочки импликаций, доказательство разбором случаев.

35.Суперпозиция функций алгебры логики.

36. Полные системы функций. Понятие базиса.

37.Алгебра Жегалкина. Полином Жегалкина. Теорема Жегалкина.

38.Замкнутые классы функций.

39. Линейные функции.

40. Монотонные функции. Теорема о монотонных функциях.

41.Двойственность в алгебре высказываний. Самодвойственные функции.

42.Функции не сохраняющие константы 0, 1.

43.Теорема Поста о функциональной полноте.