Расчет сварных соединений с угловыми швами
Сварные соединения элементов конструкций обладают рядом преимуществ по сравнению с болтовыми и заклепочными соединениями. Они не создают ослаблений соединяемых элементов отверстиями, менее трудоемки в изготовлении и поэтому являются более технологичными.
Принципы расчета сварного соединения рассмотрим на примере соединения внахлестку двух стальных листов с помощью угловых швов, которые в основном работают на срез (рис 5.5).
Будем считать, что передача усилия Nc одного из свариваемых элементов на другой происходит равномерно по длине шва.
Обычно предполагается, что поперечное сечение углового шва (если не учитывать наплыв металла в виде валика) представляет собой прямоугольный треугольник с катетом, равным 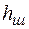 (рис. 5.5, б, в). При сдвиге одного из соединяемых элементов относительного другого наиболее вероятен срез по наименьшей площади продольного сечения шва, проходящего через биссектрису прямого угла. Эта площадь (на рис. 5.5, б она заштрихована) равна
(рис. 5.5, б, в). При сдвиге одного из соединяемых элементов относительного другого наиболее вероятен срез по наименьшей площади продольного сечения шва, проходящего через биссектрису прямого угла. Эта площадь (на рис. 5.5, б она заштрихована) равна
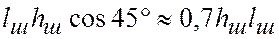 ,
,
где 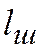 — расчетная длина шва, принимаемая с учетом непровара концов шва, меньше его полной длины на 10 мм.
— расчетная длина шва, принимаемая с учетом непровара концов шва, меньше его полной длины на 10 мм.
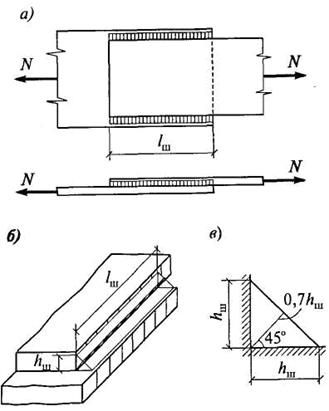
Рис. 5.5
С учетом сказанного расчетное усилие, которое может быть воспринято одним швом из условия прочности при срезе, определяется по формуле
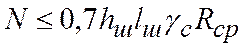 , (5.7)
, (5.7)
где Rcp — расчетное сопротивление углового шва на срез по металлу шва.

 2. КРУЧЕНИЕ ВАЛОВ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
2. КРУЧЕНИЕ ВАЛОВ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Кручением называется такой вид деформации, при котором в поперечном сечении вала возникает только крутящий момент 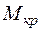 , а все остальные внутренние силовые факторы равны нулю.
, а все остальные внутренние силовые факторы равны нулю.
На кручение работают валы двигателей и станков, оси моторных вагонов и локомотивов, винтовые пружины и т.п.
Рассмотрим прямой стержень круглого поперечного сечения, левый конец которого жестко закреплен, а к свободному правому концу приложен скручивающий (вращающий) момент М (рис. 5.8, а). В заделке возникает реактивный момент противоположного направления.
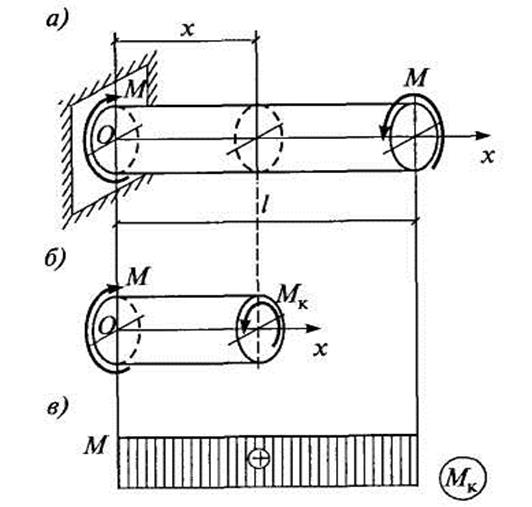
Рис. 5.8
Для определения крутящего момента используем метод сечений (рис. 5.8, б). Под действием скручивающего момента М в произвольном сечении возникает крутящий момент Мк, постоянный по длине стержня. Крутящий момент будем считать положительным, если при взгляде на сечение со стороны его внешней нормали он направлен против хода часовой стрелки. Закон изменения крутящих моментов по длине стержня изображается графически с помощью эпюры крутящих моментов. В данном случае крутящий момент постоянен по длине стержня (рис. 5.8, в).
К стержню может быть приложено несколько скручивающих моментов (рис. 5.9, а). Так как стержень и любая его часть находятся в равновесии, то алгебраическая сумма скручивающих моментов, приложенных к каждой части стержня, должна быть равна нулю. Из уравнения равновесия всего стержня определим реактивный момент МА в заделке.
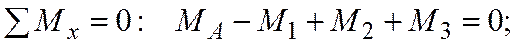
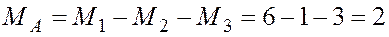 кНм.
кНм.
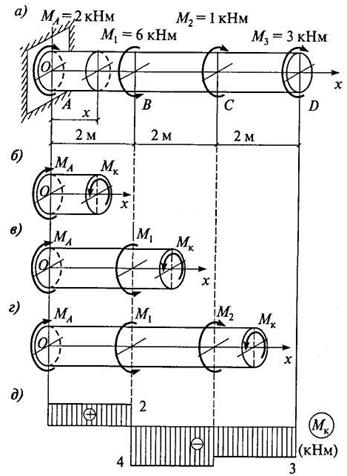
Рис. 5.9
Участок АВ 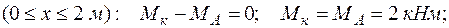
Участок ВС 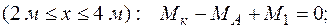
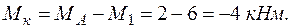
Участок CD 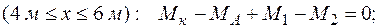
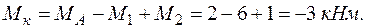
Эпюра крутящих моментов показана на рис. 5.9, д.
Напряжения в стержне круглого поперечного сечения при кручении. Рассмотрим стержень круглого поперечного сечения, защемленный левым концом и нагруженный на правом конце скручивающим моментом М (рис. 5.11).При кручении образующая АВ на боковой поверхности стержня превратится в винтовую линию АВ1. Поперечное сечение стержня, находящееся на расстоянии х от заделки, повернется на угол φ, а соседнее с ним сечение — на угол φ + dφ. Угол φ называется углом закручивания, а производная отφ по х — относительным углом закручивания
Экспериментальные и теоретические исследования кручениякруглых стержней дают основание принять следующие гипотезы:
