Действия над комплексными числами, записанными в алгебраической форме

Раздел 1. Элементы аналитической геометрии, высшей и линейной алгебры.

(5 тем)

Тема: Комплексные числа

Методические разработки для студентов.

Методические материалы к практическим занятиям для студентов.

Дисциплина: Математический анализ.

Тема: Комплексные числа. Многочлены

Учебные элементы темы.

1. Комплексные числа и действия над ними. Определение, свойства, операции на ними. Алгебраическая и тригонометрическая формы комплексного числа. Формула Муавра. Показательная форма комплексного числа. Формула Эйлера.

2. Многочлены. Основная теорема алгебры. Разложение многочлена на множители. Теорема Безу.

Разложение дробно-рациональной функции на сумму простых дробей.

Литература для самостоятельного изучения.

1.Сборник задач по математике (для втузов). Под ред. А.В Ефимова , Б.П.Демидовича, 1993г. Гл1. Стр.39.

2.И.Н.Коновалова и др. Комплексные числа и их приложения.. Учебное пособие Кафедра Высшей математики МБФ, ГОУ ВПО РГМУ Росздрава 2007 г.

3. Письменный Д.Т. Лекции по высшей математике. , стр 285.

4. Задачи для обязательного решения дома представлены в конце методички.

Вопросы для самостоятельной подготовки по теме

«Комплексные числа»

1. Сформулировать основные определения комплексного числа и формы представления.

2. Как записывается комплексное число в алгебраической (тригонометрической) форме и по каким правилам проводятся арифметические операции над ними

3. Что означает в определении комплексного числа фраза «упорядоченная пара действительных чисел»?

4. 3. Какое из этих чисел называется «действительной частью Re z», какое «мнимой Imz»?

5. В каком случае комплексное число является обычным действительным числом?

6. При каких условиях считается , что два комплексных числа равны?

7. По каким правилам осуществляются действия и находятся: сумма, разность, произведение и частное двух комплексных чисел?

8. Какое комплексное число называется сопряженным к заданному и какими свойствами оно обладает?

9. Что называют «мнимой единицей» , как ее обозначают, и что получается при возведении ее в старшую степень ?

10. Что называют комплексной плоскостью, действительной и мнимой осями и как изображается комплексное число на комплексной плоскости?

11. Что называют «модулем» и «аргументом» комплексного числа? Каковы их возможные значения для множества точек комплексной плоскости?

12. В каких пределах значений находится «главное значение аргумента комплексного числа?

13. Запишите комплексное число в алгебраической и тригонометрической формах, а также основные соотношения связывающие их.

14. По каким правилам осуществляются действия над комплексными числами в тригонометрической форме: произведение, возведение в степень, деление?

15. Какой вид имеет формула Муавра при возведении комплексного числа в натуральную степень?

16. Что называют « корнем n- степени из комплексного числа» ?

17. Сколько возможных значений имеет корень степени n=5 из комплексного числа z= 1-2i ?

18. Как выглядит общая формула Муавра для извлечения корня n- степени из комплексного числа ?

19. Как выглядит показательная форма комплексного числа и записывается формула Эйлера?

20. С помощью формулы Эйлера запишите операции умножения, деления, возведения в степень и извлечения корня.

§ 1.Теоретическое введение

Определение. Комплексным числом zназывается упорядоченная пара чисел (а,b), над множеством которых по определенным правилам можно производить следующие операции: сложение , умножение, деление, возведение в степень результаты которых также являются комплексными числами.

Определение. Алгебраической формой компле5ксного числа zназывается выражение 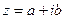, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:

При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).

Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.

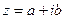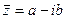Определение. Числа и называются комплексно – сопряженными.

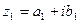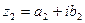Определение. Два комплексных числа и называются равными, если соответственно равны их действительные и мнимые части:

Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.

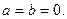
Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.

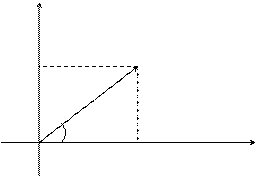
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, (комплексной плоскости z) координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.

у

A(a, b)

r b

j

0 a x

Таким образом, на оси ОХ располагаются действительные числа a, а на оси ОY – чисто мнимые-b.

С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.

Тригонометрическая форма числа.

Из геометрических соображений видно, что 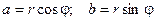. Тогда комплексное число можно представить в виде:

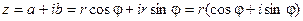
Такая форма записи называется тригонометрической формой записи комплексного числа.

При этом величина r называется модулемкомплексного числа, а угол наклона j -аргументомкомплексного числа.

.

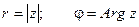Из геометрических соображений видно:

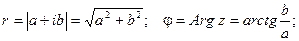
Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.

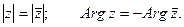
Действия с комплексными числами.

Основные действия с комплексными числами вытекают из действий с многочленами.

1) Сложение и вычитание.

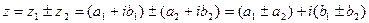
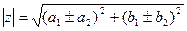
2) Умножение.

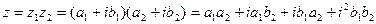
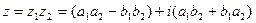
В тригонометрической форме:

,

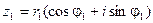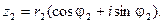
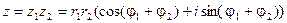
С случае комплексно – сопряженных чисел:

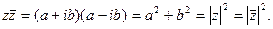
3) Деление.

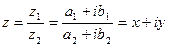
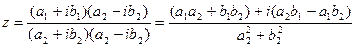
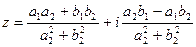
В тригонометрической форме:

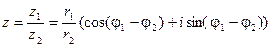
4) Возведение в степень.

Из операции умножения комплексных чисел следует, что

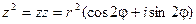
В общем случае получим:

,

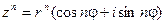где n – целое положительное число.

Это выражение называется формулой Муавра.

(Абрахам де Муавр (1667 – 1754) – английский математик)

Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.

Пример. Найти формулы sin2j и cos2j.

Рассмотрим некоторое комплексное число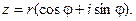

Тогда с одной стороны .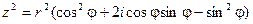

По формуле Муавра: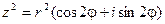

Приравнивая, получим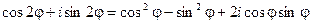

Т.к. два комплексных числа равны, если равны их действительные и мнимые части, то

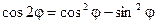
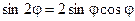
Получили известные формулы двойного угла.

5) Извлечение корня из комплексного числа.

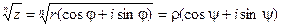
Возводя в степень, получим:

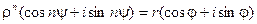
Отсюда: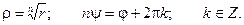

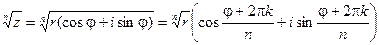
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.

Показательная форма комплексного числа.

Рассмотрим показательную функцию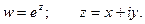

Можно показать, что функция w может быть записана в виде:

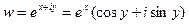
Данное равенство называется уравнением Эйлера.Вывод этого уравнения будет рассмотрен позднее.

Для комплексных чисел будут справедливы следующие свойства:

1)

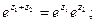
2)

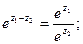
3) 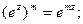где m – целое число.

Если в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то получаем:

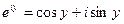
Для комплексно – сопряженного числа получаем:

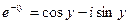
Из этих двух уравнений получаем:

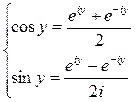
Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции кратных углов.

Если представить комплексное число в тригонометрической форме:

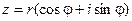
и воспользуемся формулой Эйлера: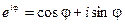

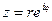
Полученное равенство и есть показательная форма комплексного числа.

Разложение многочлена на множители.

Определение. Функция вида f(x) 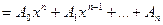называется целой рациональной функцией от х.

Теорема Безу. (Этьенн Безу (1730 – 1783) – французский математик)

При делении многочлена f(x) на разность ( x – a) получается остаток, равный f(a).

Доказательство. При делении многочлена f(x) на разность ( x – a) частным будет многочлен f₁(x) степенина единицу меньшей, чем f(x), а остатком – постоянное число R.

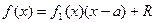
Переходя к пределу при х ® a, получаем f(a) = R.

Следствие. Если, а – корень многочлена, т.е. f(a) = 0, то многочлен f(x) делится на (х – а) без остатка.

Определение. Если уравнение имеет вид Р(х) = 0, где Р(х) – многочлен степени n, то это уравнение называется алгебраическим уравнением степени n.

Теорема. (Основная теорема алгебры) Всякая целая рациональная функция f(x) имеет, по крайней мере, один корень, действительный или комплексный.

Теорема. Всякий многочлен n – ой степени разлагается на n линейных множителей вида (x – a) и множитель, равный коэффициенту при xⁿ.

Теорема. Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.

Если среди корней многочлена встречаются кратные корни, то разложение на множители имеет вид:

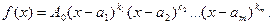
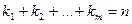
k_i - кратность соответствующего корня.

Отсюда следует, что любой многочлен n – ой степени имеет ровно n корней (действительных или комплексных).

Это свойство имеет большое значение для решения алгебраических уравнений, дифференциальных уравнений и играет важную роль в анализе функций.

Рассмотрим несколько примеров действий с комплексными числами.

Пример. Даны два комплексных числа 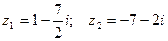. Требуется а) найти значение выражения 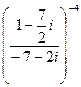в алгебраической форме, б) для числа 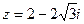найти тригонометрическую форму, найти z²⁰, найти корни уравнения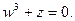

a) Очевидно, справедливо следующее преобразование:

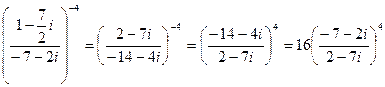
Далее производим деление двух комплексных чисел:

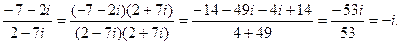
Получаем значение заданного выражения: 16(-i)⁴ = 16i⁴ =16.

б) Число 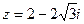представим в ви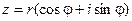де , где

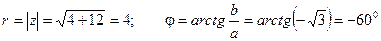
Тогда .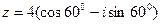

Для нахождения 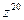воспльзуемся формулой Муавра.

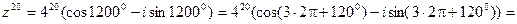
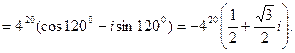
Если 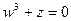, то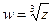

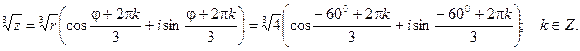
Действия над комплексными числами, записанными в алгебраической форме

Алгебраической формой комплексного числа z = (a, b).называется алгебраическое выражение вида

z = a + bi.

Арифметические операции над комплексными числами z₁= a₁+ b₁i и z₂= a₂+ b₂i, записанными в алгебраической форме, осуществляются следующим образом.

1. Сумма (разность) комплексных чисел

z₁± z₂= (a₁± a₂) + (b₁±b₂)∙i,

т.е. сложение (вычитание) осуществляются по правилу сложения многочленов с приведением подобных членов.

2. Произведение комплексных чисел

z₁∙z₂= (a₁∙a₂- b₁∙b₂) + (a₁∙b₂+ a₂∙b₁)∙i,

т.е. умножение производится по обычному правилу умножения многочленов, с учетом того, что i²=1.

3. Деление двух комплексных чисел осуществляется по следующему правилу:

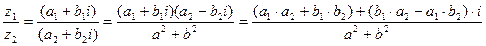, (z₂ ≠ 0),

т.е. деление осуществляется умножением делимого и делителя на число, сопряженное делителю.

Возведение в степень комплексных чисел определяется следующим образом:

.

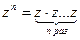Легко показать, что

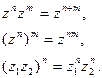
Примеры.

1. Найти сумму комплексных чисел z₁= 2 – i и z₂= –4 + 3i.

z₁+ z₂= ( 2 + (–1)∙i )+ (–4 + 3i ) = ( 2 + (–4)) + ((–1) + 3 ) i = –2+2i.

2. Найти произведение комплексных чисел z₁= 2 – 3i и z₂= –4 + 5i.

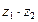₌ ( 2 – 3i ) ∙ (–4 + 5i ) = 2 ∙(–4) + (-4) ∙(–3i)+ 2∙5i – 3i∙5i =7+22i.

3. Найти частное z от деления z₁= 3 – 2на z₂ = 3 – i.

z = .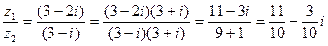

4. Решить уравнение: 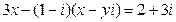, x и y Î R.

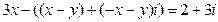
(2x + y ) + ( x + y )i = 2 + 3i.

В силу равенства комплексных чисел имеем:

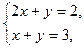
откуда x = –1 , y = 4.

5. Вычислить: i², i³, i⁴, i⁵, i⁶, i^-1 , i^-2.

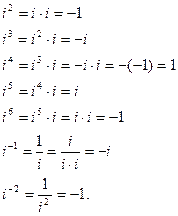
6. Вычислить 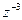, если .

.

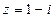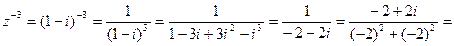
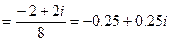7. Вычислить число 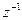обратное числу z =3-i.

.
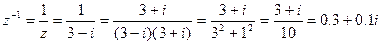